UNIWERSYTET WARMIŃSKO - MAZURSKI W OLSZTYNIE Olsztyn, 17.03.2009 r.

WYDZIAŁ GEODEZJI I GOSPODARKI PRZESTRZENNEJ

KIERUNEK: GEODEZJA I SZACOWANIE NIERUCHOMOŚCI

Sprawozdanie 1

Koncentracja zjawisk przestrzennych

Łukasz Chmielewski Rok II Grupa

Wskazanie jednostek w których koncentracja jest: największa, najmniejsza

Wody otwarte

Jednostki o największej koncentracji:

• Gębałka (1) - 2,50

• Harsz (2) - 2,45

Jednostki o najmniejszej koncentracji:

• Krzywińskie (4) - 0,03

• Wyłudy (12) - 0,04

• Kuty (5) - 0,08

Lasy i zadrzewienie

Jednostki o największej koncentracji:

• Kuty (5) - 2,54

• Przerwanki (9) - 1,63

• Pozezdrze (8) - 1,24

Jednostki o najmniejszej koncentracji:

• Piłaki Wlk. (7) - 0,04

• Gębałka (1) - 0,06

Wody, lasy i zadrzewienie

Jednostki o największej koncentracji:

• Kuty (5) - 1,48

• Harsz (2) - 1,42

• Przerwanki (9) - 1,16

• Gębałka (1) - 1,11

Jednostki o najmniejszej koncentracji:

• Piłaki Wlk. (7) - 0,08

• Krzywińskie (4) - 0,24

Koncentracja zjawisk przestrzennych

.

Zasady obliczania i zastosowanie współczynnika koncentracji:

Stosowany jest do badań koncentracji zjawiska na tle układu regionalnego innego zjawiska. Koncentracja ma pewne korzyści, ale po przekroczeniu jej optymalnego punktu, dostrzegamy straty i niepożądane rzeczy. Z porównania układów wynika, w jakim stopniu skupienie badanego zjawiska odchyla się od skupienia zjawiska podstawowego. Współczynnik ma postać:

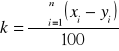
gdzie:

- x_i - oznacza procentowy udział obszaru cząstkowego i w wartości globalnej badanego zjawiska na obszarze całkowitym,

- y_i - oznacza procentowy udział obszaru cząstkowego i w wartości globalnej zjawiska podstawowego na obszarze całkowitym,

- n - oznacza liczbę obszarów cząstkowych.

Współczynnik koncentracji jest miarą niemianowaną i waha się od zera, gdy zjawisko badane jest rozmieszczone tak jak zjawisko podstawowe ( taki stan nazywa się pełną dyspersją), do jedności, gdy zjawisko badane skupione jest na jednym obszarze cząstkowym (taki stan z kolei określany jest mianem pełnej koncentracji).

Wartość obliczonego współczynnika koncentracji ma swoje graficzne odbicie w krzywej koncentracji (LORENZA). Jeśli badane zjawisko jest rozmieszczone równomiernie, to otrzymujemy prostą nachyloną pod kątem 45° wychodzącą z początku układu współrzędnych. Każde odchylenie od proporcjonalności powoduje, że krzywa staje się wypukła. Możemy z tego wywnioskować, że im większe jest odchylenie, czyli im bardziej badane zjawisko przestrzenne skoncentrowane jest w niewielu jednostkach badawczych, tym bardziej wypukłe kształty przybiera krzywa koncentracji.

Miarą koncentracji jest powierzchnia zawarta między prostą nachyloną pod kątem 45° wychodzącą z początku układu współrzędnych i krzywą koncentracji. Stosunek tej powierzchni do całkowitej powierzchni górnego trójkąta wykresu jest równy współczynnikowi koncentracji.

Proces tworzenia wykresu:

• Zestawienie badanych jednostek w kolejności według wielkości ilorazu lokalizacji, zaczynając od największego. Iloraz lokalizacji jest ilorazem udziału procentowego badanego zjawiska i udziału procentowego zjawiska podstawowego.

• Kumulacja procentów dla każdego szeregu.

• Naniesienie skumulowanego szeregu reprezentującego badane zjawisko na oś pionową,

a skumulowanego szeregu reprezentującego zjawisko podstawowe na oś poziomą.

Wnioski:

• Dotyczące zastosowanej metody:

Metoda ta jest metodą ilościową, a nie jakościową. Ma na celu wstępną kwalifikację terenu na określony cel na podstawie jedynie ilości a nie jakości występujących cech. Pozwala to nam wybrać rejony, w których występują podstawowe walory i których poszukujemy. Niestety metoda ta tylko wskazuje tereny, gdzie dane zjawisko występuje najpowszechniej i w największej ilości. Nie mamy żadnych wiadomości na temat jakości, przydatności, zniszczenia czy dostępności danego waloru, co skutecznie i całkowicie może wykluczyć badany teren z listy tych najlepszych, mimo że metoda koncentracji zjawisk przedstawia dany obszar jako najlepszy. Dlatego ta metoda może służyć tylko do wstępnej analizy przydatności zjawiska.

• Dotyczące wyników:

Uzyskane wyniki wskazują, że w przypadku wód otwartych współczynnik koncentracji wynosi 0,48 co jest całkiem wysoką wartością, a to z kolei świadczy o nierównomiernym rozmieszczeniu waloru (przedstawione na Rys.2). Największą wartość osiąga iloraz lokalizacji w obrębach Gębałka oraz Harsz, co w konsekwencji odbija się dużą możliwością rozwoju turystyki, rekreacji i wypoczynku związanego z wodą. Bardzo źle na tle wyżej wymienionych obrębów wypadają Krzywińskie, Wyłudy oraz Kuty. Na obszarach tych wszelka forma wypoczynku oraz rekreacji jest praktycznie nieosiągalna, nie do zrealizowania, z powodu braku głównego waloru, który mógłby przyciągnąć turystów pragnących wypoczywać nad wodą.

Z wykresu nr 3 możemy zauważyć, że lasy i zadrzewienie są rozłożone bardziej równomiernie od wód. Świadczy o tym mniejsza wypukłość wykresu nr 3 od nr 2. Współczynnik koncentracji wynosi 0,25, więc jest niemal dwukrotnie mniejszy od współczynnika dla wód. Najwyższy iloraz lokalizacji jest w obrębie Kuty i wynosi ok. 2,54. Następny obręb (Przerwanki) ma już dużo niższy iloraz bo 1,63 i głównie one wraz z jeszcze jedynie paroma obrębami mogą zostać zakwalifikowane do dalszej oceny. Bardzo słabo pod tym względem wypadają Piłaki Wlk. oraz Gębałka.

Obliczając współczynnik koncentracji jezior, lasów i zadrzewienia otrzymaliśmy współczynnik koncentracji ilustrujący oba te zjawiska razem na danym obszarze. Współczynnik rzędu 0,18 jest niższy od tych, które otrzymaliśmy do tej pory. Dzięki takiemu zestawieniu określiliśmy natężenie występowania obydwu elementów w poszczególnych jednostkach badawczych. Obręby Kuty, Harsz i Przerwanki mogą się poszczycić najwyższymi ilorazami lokalizacji, słabo natomiast wypadają Piłaki Wlk. i Krzywińskie. Wykres nr 1 dotyczący przestrzennej koncentracji wód otwartych, lasów i zadrzewienia na tle powierzchni ogólnej gminy Pozezdrze jest najmniej wypukły co świadczy o większej równomierności rozmieszczenia walorów.

---