RACHUNEK PRAWDOPODOBIEŃSTWA I STATYSTYKA

Należy powtórzyć:

• określenie i własności - permutacji bez powtórzeń, kombinacji bez powtórzeń, wariacji z powtórzeniami i bez powtórzeń;

• definicja klasyczna prawdopodobieństwa;

• własności prawdopodobieństwa;

• twierdzenie o prawdopodobieństwie całkowitym;

• twierdzenie o prawdopodobieństwie warunkowym;

• twierdzenie - schemat Bernoulliego;

• średnie - arytmetyczna, geometryczna, harmoniczna, ważona;

• modalna;

• mediana;

• wariancja;

• odchylenie standardowe.

1. Oblicz, ile różnych liczb trzycyfrowych można utworzyć z cyfr 0,1,2,3,4 ,jeżeli każda cyfra może wystąpić tylko jeden raz.

2. Z cyfr: 2, 4, 5, 6 układamy liczby 3-cyfrowe podzielne przez 4, w których każda cyfra może wystąpić tylko raz. Ile liczb można utworzyć?

3. Ile mających sens lub słów można ułożyć z liter słowa PARAPET.

4. Rozwiąż równania: a)
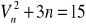
   b)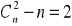
   c)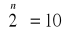
   .

5. Oblicz, ile różnych liczb trzycyfrowych można utworzyć z cyfr 0,1,2,3,4,5 jeżeli

a) każda cyfra może wystąpić tylko jeden raz

b) cyfry mogą się powtarzać .

6. Wiadomo, że P(A)=3/25, zaś P(B')=7/10 i P(A჈B)=4/10. Oblicz P(AჇB), P(A-B), P(A'ჇB).

7. Z tali 52 kart losujemy jedną. Jakie jest prawdopodobieństwo, że jest to :

1. As

2. karta kier

3. figura

4. karta starsza od 10 lub koloru pik?

8. Rzucamy dwiema kostkami do gry. Oblicz prawdopodobieństwo, że

1. suma wyrzuconych oczek jest równa 7

2. na przynajmniej jednej kostce wypadła liczba oczek większa od 4.

9. W urnie jest n kul, w tym 5 kul białych. Z urny losujemy dwie kule. Jakie musi być n , aby prawdopodobieństwo, że obie wylosowane kule są białe było większe od 1/3?

10. W kolejce do kasy ustawiło się losowo 10 osób, wśród nich Jacek, Ewa i Ania. Jakie jest prawdopodobieństwo, że będą oni stać obok siebie?

11. Oblicz prawdopodobieństwo zdarzenia, że w skład 5-osobowej delegacji wejdzie co najmniej 4 chłopców, jeżeli jest ona wybrana z grupy składającej się z 6 chłopców i 4 dziewcząt.

12. Z tali 52 kart wylosowano jedną. Jakie jest prawdopodobieństwo tego, że jest to siódemka, jeżeli wiadomo, że wyciągnięta karta nie jest figurą ani asem?

13. Z urny, w której znajduje się 5 kul białych, 3 czarne oraz 2 zielone losujemy kolejno bez zwracania dwie kule. Jakie jest prawdopodobieństwo, że:

1. obie wylosowane kule są białe

2. za drugim razem wylosujemy kulę zieloną , jeśli za pierwszym razem wylosowaliśmy kulę czarną .

14. W pewnej hurtowni sprzedaje się produkty dwóch fabryk, przy czym z fabryki I pochodzi 25% z zaopatrzenia. Fabryka I wśród swoich wyrobów ma 75% ze znakiem jakości ISSO, a fabryka II 30% ze znakiem jakości ISSO. Oblicz prawdopodobieństwo , że kupiony w tej hurtowni artykuł ma znak jakości ISSO.

15. Z urny zawierającej 3 kule białe , 4 kule czerwone i 8 kul zielonych losujemy jedną kulę. Następnie zwracamy do urny kulę wylosowaną i dokładamy jeszcze 5 kul w kolorze tej kuli, którą wylosowaliśmy. Ponownie losujemy 1 kulę. Oblicz prawdopodobieństwo, że będzie to kula zielona.

16. Rzucamy dwukrotnie symetryczną monetą. Jeśli wypadnie przynajmniej 1 orzeł to losujemy jedną kulę z urny zawierającej 2 kule niebieskie i 5 zielonych, w pozostałych przypadkach losujemy kulę z urny zawierającej po 4 kule niebieskie i zielone. Oblicz prawdopodobieństwo wylosowania kuli zielonej.

17. Z urny, w której znajduje się 3 kule białe i 4 czerwone, losujemy pięć razy po dwie kule, zwracając każdą wylosowaną parę do urny. Jakie jest prawdopodobieństwo, że

1. cztery razy wylosujemy parę kul tego samego koloru

2. przynajmniej 4 razy otrzymamy parę kul różnych kolorów

3. co najwyżej raz otrzymamy parę kul czerwonych.

18. Rzucamy cztery razy sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia, że co najmniej w jednym rzucie wypadnie 6 oczek.

19. Rzucamy 10 razy symetryczną monetą. Oblicz prawdopodobieństwo otrzymania orła dwa lub trzy razy.

20. Na podstawie podanych danych wzrostu uczniów pewnej klasy wyznacz medianę i modę ich wzrostu.

A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	R	S	T	U
170	165	167	174	158	167	170	159	164	172	181	169	170	164	179	170	175	178	159	164

Naszkicuj wykres ilustrujący ile osób jest poszczególnego wzrostu.

21. W tabeli podano dane z kantorów w Poznaniu. Na podstawie tych danych oblicz średnią cenę skupu $ w Poznaniu. W ilu kantorach w tym mieście $ kupowano drożej od wyznaczonej ceny średniej?

cena skupu $ w zł	3,51	3,52	3,53	3,54	3,55
liczba kantorów	10	3	4	2	5

22. Na wykresie przedstawiono wyniki matury z matematyki

1. Jaki % uczniów zdających maturę z matematyki uzyskało ocenę niższą od 3,

2. wyznacz średnią ocen z matematyki,

3. jaki % uczniów zdających matematykę uzyskało ocenę nie niższą niż średnia?




23. Wyznacz wariancję i odchylenie standardowe dla stopni Joanny z historii:

l.p.	stopień
1	5
2	4
3	4
4	3
5	3
6	2
7	2

---