Ruch jednostajny po okręgu

Jeżeli prędkość kątowa punktu poruszającego się po okręgu nie zmienia się, to ruch nazywamy ruchem jednostajnym po okręgu.

W ruchu jednostajnym po okręgu
ω  = const oraz  v = const (prędkość liniowa jest stała), a także
|v| = const.

Przykładem ruchu jednostajnego po okręgu może być ruch poproszka leżącego na obracającej się płycie gramofonowej, lub ruch obiektu leżącego na powierzchni obserwowany z bieguna ziemskiego w układzie nie obracającym się wraz z Ziemią (np. wtedy, gdy jedna oś układu odniesienia cały czas jest zwrócona na Słońce lub odległą gwiazdę).

Więcej o ruchu jednostajnym po okręgu

W ruchu jednostajnym po okręgu przyspieszenie (jako wektor) nie jest równe zero, mimo że wartość prędkości nie zmienia się. Z dwóch składowych przyspieszenia: stycznej i normalnej tylko jedna ma wartość zero.

	składowa styczna (zmieniająca wartość prędkości) ma wartość zero
	składowa normalna (zmieniająca kierunek prędkości) jest niezerowa

Jest tak, ponieważ kierunek prędkości ulega ciągłej zmianie - prędkość musi być ciągle zakrzywiana do środka okręgu. Dlatego z ruchem jednostajnym po okręgu związana jest stała wartość przyspieszenia nazywanego przyspieszeniem dośrodkowym.Prędkość kątowa Podczas ruchu po okręgu wraz z przebywaną drogą ∆L, zmienia się kąt pod jakim obserwowany jest poruszający się obiekt  ∆α, dlatego celowe jest wprowadzenie wielkości charakteryzującej szybkość zmiany kąta. Wielkością tego rodzaju jest tzw. prędkość kątowa. Oznaczamy ją ω (mała grecka litera omega).

ω - prędkość kątowa (układzie SI w rad/s, lub 1/s = 1 s^-1)
∆α - kąt zakreślony przez promień wodzący (w radianach)
∆t - czas w jakim odbywa się ruch, lub jego fragment (w układzie SI sekundach s). Prędkość kątowa jest równa kątowi zakreślonemu podczas ruchu podzielonemu przez czas.Jednostki prędkości kątowejPrędkość kątowa w jednostkach układu SI wyrażana jest w radianach na sekundę: [ω] = rad/s = 1/sZwiązek między prędkością liniową i prędkością kątową

Pomiędzy prędkością liniową punktu poruszającego się po okręgu, a prędkością kątową istnieje prosta zależność:

W=v/r

Znaczenie symboli:

ω  - prędkość kątowa (w rad/s, lub opuszczając radiany 1/s = s^-1)
R - promień okręgu którego fragmentem jest zakreślany łuk (najczęściej w metrach m).
v - prędkość liniowa, czyli „zwykła” prędkość punktu (najczęściej w m/s)

Zależność odwrotna

Z wyżej wypisanego wzoru można wyliczyć prędkość liniową v. W rezultacie dostaniemy wzór:

v = ω R

Wyprowadzenie

1. Do wzoru na prędkość kątową podstawiamy definicję kąta:

 

2. uwzględniamy że prędkość liniowa to:

 

3. więc ostatecznie:

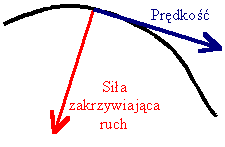
Przyspieszenie dośrodkoweCiało na które nie działa żadna siła pozostaje w spoczynku, lub porusza się ruchem jednostajnym prostoliniowym. Jeżeli siła działa w kierunku ruchu, to nie będzie ona zakrzywiać toru - ruch będzie cały czas prostoliniowy (opóźniony, lub przyspieszony).

W przypadku jednak gdy ma składową skierowaną pod kątem do kierunku ruchu (lub inaczej mówiąc ma jakąś składową prostopadłą do prędkości) to ruch będzie się zakrzywiał. W takiej sytuacji mamy do czynienia z przyspieszeniem dośrodkowym.  Pomiędzy promieniem krzywizny zakrzywienia (promieniem okręgu po którym porusza się obiekt), a prędkością ruchu i zakrzywiającym przyspieszeniem zachodzi związek:Wzór na przyspieszenie dośrodkowe

   

v  - prędkość w ruchu po okręgu (w układzie SI w m/s)
R  - promień okręgu (w układzie SI w m)Powyższy wzór najprościej jest odnieść do ruchu jednostajnego po okręgu.

W tym przypadku promień krzywizny jest po prostu promieniem okręgu, a środek krzywizny jest o prostu środkiem okręgu. Dla ruchów o torach bardziej skomplikowanych promień krzywizny będzie zmieniał w trakcie ruchu i jest określony tylko dla każdego punktu osobno.   Znaczenie symboli: Dla ruchu po okręgu: Znaczenie symboli: v - prędkość ruchu po okręgu (w układzie SI w m/s) R - promień okręgu (w układzie SI w m) adośr - przyspieszenie dośrodkowe ruchu po okręgu (w układzie SI w m/s^2) Dla dowolnych ruchów krzywoliniowych   Znaczenie symboli: v - prędkość ruchu w danym momencie (w układzie SI w m/s) R - promień krzywizny toru (w układzie SI w m) adośr - przyspieszenie dośrodkowe zakrzywiające tor ruchu, lub inaczej przyspieszenie normalne w tym ruchu (w układzie SI w m/s^2) Jeżeli w miejsce prędkości liniowej podstawimy   v = ω·R   to otrzymamy drugi wzór na wartość przyspieszenia dośrodkowego: adośr = ω^2 ∙ R

Okres ruchu po okręgu Okres ruchu po okręgu (T) jest to czas, po którym punkt materialny wykona jeden pełny obieg całego okręgu. Jednostką okresu jest sekunda (minuta, godzina...)  [T] = s Jeżeli punkt materialny wykonuje N obiegów okręgu w ciągu czasu t, wtedy oczywiście okres dany jest wzorem:   Znaczenie symboli: T - okres ruchu (w sekundach s) N - ilość wykonanych (również niepełnych, wtedy liczba będzie ułamkiem) okrążeń okręgu (liczba niemianowana) t - czas w jakim odbywa się ruch, lub jego fragment (w sekundach s)   Częstotliwość ruchu obrotowego i ruchu po okręgu Częstotliwość (f) jest to ilość obiegów okręgu wykonanych w jednostce czasu. Jednostką częstotliwości jest jeden herc [f] = Hz = 1/s Jeżeli punkt materialny wykonuje N obiegów okręgu w ciągu czasu t, to częstotliwość wyliczymy ze wzoru:   Znaczenie symboli: f - częstotliwość (w Hz = 1/s = s^-1) N - ilość wykonanych (również niepełnych - wtedy pojawi się ułamek) okrążeń okręgu (liczba niemianowana) t - czas w jakim odbywa się ruch, lub jego fragment (w sekundach s) Związek między okresem i częstotliwością ruchu po okręgu Z porównania obu tych definicji wynika, że:   Użyteczne też mogą być wzory wyrażające prędkość kątową w ruchu po okręgu za pomocą częstotliwości, lub okresu: ω = 2 π f      Uwaga: Wzór na prędkość kątową jest identyczny ze wzorem na częstość kołową ruchu drgającego. Częstość kołowa ma również to samo oznaczenie co prędkość kątowa. Ta zbieżność nie jest przypadkowa, ponieważ istnieje ścisła odpowiedniość między ruchem po okręgu, a ruchem drgającym harmonicznym (odnosi się to także do ruchu falowego).

---