Metoda Pawłowskiego

W metodzie tej wybiera się taką kombinacje zmiennych objaśniających, która z jednej strony gwarantuje pewną z góry, ustaloną dokładność opisu zmiennej objaśnianej, z drugiej zaś ogranicza wzajemne skorelowanie zmiennych objaśniających.

Przyjmując, że w wyniku przeprowadzenia doboru zmiennych objaśniających do modelu wyszczególniono p zmiennych kandydujących. Procedura wyboru zmiennych do modelu prezentuje się następująco:

1. Ustala się z góry liczbę k - zmiennych objaśniających, które powinny wejść do modelu,

2. Ustala się z góry wymagany poziom dokładności opisu analizowanego zjawiska przez model, tj. minimalna akceptowaną wartość R²,

3. Rozpatruje się wszystkie możliwe k elementowe kombinacje zmiennych otrzymane ze zbioru p - elementowego, których liczba wynosi
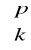
   wydzielając te wśród nich p, które spełniają narzucony warunek co do dopasowania modelu,

4. Wśród kombinacji dopuszczalnych wybiera się te, w której zmienne są najsłabiej skorelowane między sobą. W tym celu rozpatruje się podwyznaczniki macierzy korelacji między zmiennymi kandydującymi do modelu. Dla każdej z kombinacji dopuszczalnych oblicza się wartość podwyznacznika powstałego przez usunięcie z macierzy korelacji wierszy i kolumn odpowiadających zmiennym w tej kombinacji nieobecnym,

5. Za optymalną przyjmuje się taką kombinację zmiennych, dla której wartość optymalnego podwyznacznika jest największa. Wartość tego wyznacznika jest tym większa im słabiej skorelowane są zmienne objaśniające.

Przykład wyboru zmiennych metodą Pawłowskiego.

W wyniku przeprowadzenia doboru zmiennych do modelu wyodrębniono 4 zmienne kandydatki. Macierz współczynników korelacji pomiędzy zmiennymi kandydującymi przedstawia się następująco:

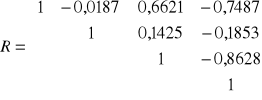
Wybierz metodą Pawłowskiego zmienne, wiedząc, że ustalono iż:

• do modelu powinny wejść 2 zmienne objaśniające,

• min wymagana wartość statystyki R² = 0,85,

• oszacowanie wartości statystyki R² dla poszczególnych kombinacji wynoszą:

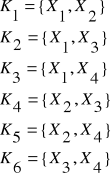
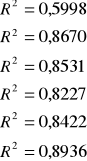
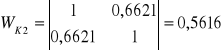
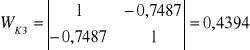
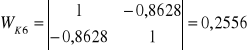
Jako zmienne objaśniające do modelu powinny wejść zmienne z K₂, tj. X₁ i X₃.