PRACA KONTROLNA 1

1. Omów wielkości mierzone w geodezji bezpośrednio w terenie

Podstawowymi wielkościami mierzonymi w terenie są odległości poziome, kąty poziome, kąty pionowe, różnice wysokości i kierunki odniesienia. W geodezji przez odległość poziomą rozumiemy długość jej rzutu na płaszczyznę poziomą ( odległość między dwoma punktami rzutowanymi na płaszczyznę). W związku z tym pomiar wykonany w terenie jednostajnie nachylonym redukujemy do poziomu. Długość lini możemy pomierzyć bezpośrednio, przez kolejne przykładanie przymiaru na wytyczonej prostej, lub pośrednio za pomocą innych wielkości, które z szukaną długością pozostają w związku funkcyjnym.

W pomiarach metodą bezpośrednią wykorzystujemy druty inwarowe i taśmy stalowe. Zmierzoną odległość stanowi odcinek: d = nl + r

gdzie: l - długość taśmy, n - liczba pełnych odłożeń, r - długość ostatniego niepełnego odłożenia taśmy (tzw. resztówka). W pomiarach długości metodą pośrednią używamy dalmierzy elektrooptycznych. Mierzona długość wynosi: D = nl + r

gdzie: l - długość fali w metrach, n - liczba ułożeń fali wzdłuż mierzonego odcinka, r - długość odpowiadająca ostatniemu niepełnemu ułożeniu fali. Dokładność pomiaru długości dalmierzami elektrooptycznymi jest bardzo duża.

Do pomiaru kątów poziomych i pionowych najczęściej używanymi instrumentami pomiarowymi są teodolit i niwelator. Kątem poziomym nazywamy kąt zawarty między rzutami kierunków na płaszczyznę poziomą i mierzony w płaszczyźnie poziomej Kątem pionowym nazywamy kąt zawarty pomiędzy kierunkiem nachylenia terenu a rzutem tego kierunku na płaszczyznę pionową i mierzony w płaszczyźnie pionowej. Podczas pomiarów niwelacyjnych mierzy się kąt pionowy h lub zenitalny z, między którymi zachodzi związek:

w podziale stopniowym: z = 90⁰ - h lub h = 90⁰ - Z

w podziale gradowym: z = 100^g - h lub h = 100^g - z

W pracach pomiarowych wchodzących w zakres geodezji na płaszczyźnie stosujemy trzy metody pomiaru kątów: - kierunkową, - pojedynczego pomiaru kąta, - repetycyjną

Różnicą wysokości nazywamy odległość od umownego punktu odniesienia do punktu na powierzchni ziemi i mierzona wzdłuż siły grawitacyjnej.

Kierunkiem odniesienia nazywamy kierunek stycznej do południka geograficznego lub magnetycznego.

2. Oblicz współrzędne prostokątne punktu P mając dane

n = 2,0

X_N = 6934,15 X_M = 7095,99 d_NP = 10,10 x n

Y_N = 3420,98 x n Y_M = 3212,44 n = 20 => d = 20,20

Y_N = 6841,96 ( bo n =2,0)

N

P

M

α = 87 ⁰26'48'' = 97^g16^c32^cc
- II ćw. A_MN = 200^g - |α| = 102,8368

X_p = X_M + ΔX_MP = X_M + d x cosA_MN

Xp = 7095,99 + 20,20 x (-0,0437) = 7095,99 - 0,88 = 7095,11

N

P Y_p = Y_M + ΔY_MP = Y_M + d x sin A_MN

A_MN

M Y_P = 3212,44 + 20,20 x (0,99) = 3212,44 + 20 = 3232,44

3. Znajdź najbardziej prawdopodobną wartość i oblicz jej błąd średni mając dane:

	v (li - Lśr)	vv
l1 = 196,75 l2 = 196,69 l3 = 196,78 - n x 10 => 196,58 l4 = 196,60 - n x 10 => 196,40	0,145 0,085 -0,025 -0,205	0,021 0,0072 0,00062 0,042
Lśr = 196,605	Σv = 0	Σvv = 0,071

Σl_i = l₁ + l₂ + l₃ + l₄ = 786,42 L_śr =

=
=
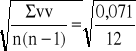
= 0,08 m - średni błąd wartości wyrównanej

=
=
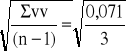
= 0,15 m - średni błąd pojedynczego spostrzeżenia

6. Oblicz pole powierzchni danej działki metodą analityczną n = 2,0

207	6059284,65 + 100n => 6059304,65	3480313,59
208	288,80	314,60
209	302,96 + 50n => 312,96	337,54
211	6059286,59	3480322,49 + 50n => 3480332,49

207 209

X		Y
1. 207 2. 208 3. 211 4. 209 5. 207	6059304,65 6059288,80 6059312,96 6059286,59 6059304,65	3480313,59 3480314,60 3480337,54 3480332,49 3480313,59

• 211

2P = X xY₂ + X₂ xY₃ + X₃ xY₄ + X₄ xY₅ - Y₁ xX₂ + Y₂ xX₃ + Y₃ xX₄ + Y₄ xX₅

2P = 6059304,65 x 3480314,60 + 6059288,80 x 3480337,54 + 6059312,96 x 3480332,49 + 6059286,59 x 3480313,59 - 3480313,59 x 6059288,80 + 3480314,60 x 6059312,96 + 3480337,54 x 6059286,59 + 3480332,49 x 6059304,65 = 202 m²

P =
= 101 m²

---