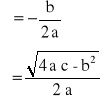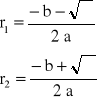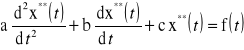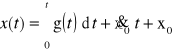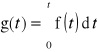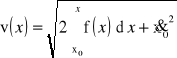Rozwiązania wybranych równań różniczkowych zwyczajnych o stałych współczynnikach Równanie typu: Rozwiązanie: gdzie: x(t) - całka ogólna równania niejednorodnego, x^*(t) - całka ogólna równania jednorodnego, x^**(t) - całka szczególna równania niejednorodnego. Tok rozwiązania Rozwiązujemy równanie jednorodne Postać całki ogólnej - x^*(t) jest uzależniona od pierwiastków równania charakterystycznego: gdzie: r - parametr równania Obliczamy wyróżnik równania charakterystycznego: Jeżeli <0, to: r1 =  + i  r2 =  - i  gdzie: Wtedy: gdzie: C1, C2 - stałe. Jeżeli rozwiązujemy tylko równanie jednorodne, to wyznacza się je z warunków początkowych

Jeżeli =0, to: wtedy: gdzie: C1, C2 - stałe. Jeżeli >0, to: wtedy: gdzie: C1, C2 - stałe. Wyznaczamy x** - całkę szczególną równania niejednorodnego   Funkcję x^**(t) przewiduje się w postaci analogicznej do funkcji f(t), tzn.: jeżeli: to:     gdzie: A - stały parametr. Parametr A ma taką wartość, że równanie: jest spełnione w każdej chwili czasu (dla każdego t). Stałe C1 i C2, występujące w całce ogólnej równania niejednorodnego, wyznaczamy z warunków początkowych.

Równanie typu: Równanie to rozwiązuje się poprzez dwukrotne całkowanie w przedziale (0,t). Po uwzględnieniu warunków początkowych: otrzymuje się rozwiązanie w postaci: gdzie: Równanie typu: Po podstawieniu: otrzymuje się równanie: Rozwiązanie tego równania, po uwzględnieniu warunku początkowego: ma postać: Ostatecznie, po scałkowaniu powyższego równania i uwzględnieniu warunku początkowego: otrzymuje się rozwiązanie w postaci:

Równanie typu: (1) Równanie to jest równaniem nieliniowym. Metodami stosowanymi w przypadku równań liniowych można je rozwiązać tylko wtedy, gdy poszukiwaną funkcją jest pochodna funkcji x(t), a więc np.: prędkość punktu materialnego: Wtedy: Równanie (1) ma więc postać: czyli po rozdzieleniu zmiennych: Po scałkowaniu i uwzględnieniu warunków początkowych: otrzymuje się rozwiązanie w postaci:

---