OKRĄG WPISANY I OPISANY NA TRÓJKĄCIE RÓWNOBOCZNYM

przykład 1 Skonstruuj trójkąt równoboczny, następnie wykonaj na tym trójkącie konstrukcję okręgu wpisanego i opisanego. (rys. poniżej)

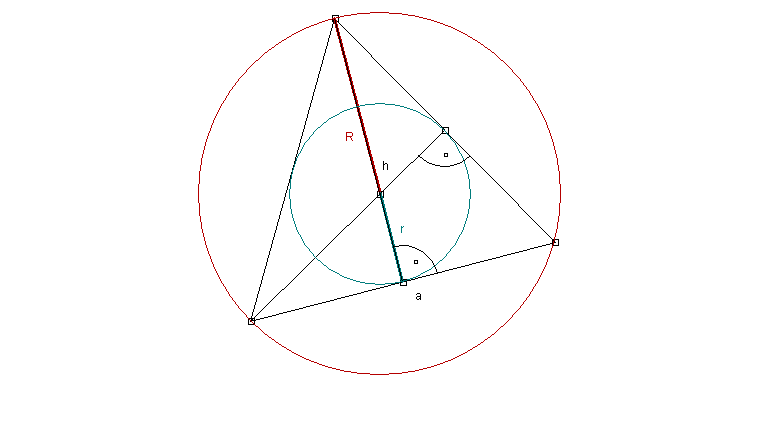
oznaczenia:
a - bok trójkąta

h - wysokość trójkąta

R - promień okręgu opisanego na trójkącie

r - promień okręgu wpisanego w trójkąt

W trójkącie równobocznym zachodzą następujące wzory:

(wzory te można uzasadnić stosując np. twierdzenie Pitagorasa)

WŁASNOŚĆ: Wysokości w trójkącie równobocznym przecinają się w punkcie, który dzieli je w stosunku 2:1.

WNIOSKI:

przykład 2 Bok trójkąta równobocznego ma długość 6cm. Oblicz:
a) pole koła opisanego na tym trójkącie
b) długość okręgu wpisanego w ten trójkąt

rozwiązanie:

a)

zatem

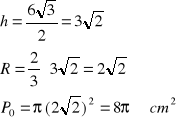
odp. Pole koła opisanego na tym trójkącie wynosi

b)

zatem:

-> wysokość została obliczona w pkt. a)

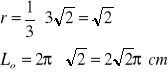
odp. Długość okręgu wpisanego w ten trójkąt wynosi

ZADANIA

1. Pole trójkąta równobocznego wynosi
. Oblicz
a) Pole koła wpisanego w ten trójkąt

b) długość okręgu opisanego na tym trójkącie

2. Pole koła opisanego na trójkącie równobocznym wynosi
. Oblicz

a) Pole tego trójkąta

b) Pole koła wpisanego w ten trójkąt

3. Długość okręgu wpisanego w trójkąt równoboczny wynosi
. Oblicz

a) Pole tego trójkąta

b) Pole koła opisanego na tym trójkącie

---