1. Substancje A i B tworzą roztwory doskonałe. W 30oC prężności par nasyconych tych związków wynoszą odpowiednio 293.1 kPa i 50 kPa. Roztwór o składzie molowym xA = 0.46 i temperaturze 30oC zamknięto w cylindrze z ruchomym tłokiem obciążonym ciśnieniem p. Obliczyć, jaki będzie stosunek liczby moli fazy ciekłej do gazowej, gdy ciśnienie będzie wynosiło 0.9 ciśnienia, w którym układ ten zaczyna wrzeć. (wynik podaj z dokładnością do 0.01)

Odpowiedź: 5

1. p wrzenia=xA*pA0 + (1-xA)*pB0

2. p=0,9 * p wrzenia

3. p=xA'*pA0+(1-xA')*pB0 => xA' = p-pB0/pA0-pB0

4. y=(xA'*pA0)/p

5. n cieczy/n pary = (y-xA)/(xA-xA')

2. Molowa pojemność cieplna pary wodnej pod stałym ciśnieniem określa równanie: Cp=28.83+13,74*10do-3T -1.435*10do-6T2 J/molK. Ile ciepła wydzieli się podczas ochładzania 155g pary wodnej od temp 390°C do100°C pod ciśnieniem 1 atm. M h2o to 18g/mol. Podać wynik w kJ

Odpowiedź: -89.56

Cp=28,83+13.74*10^-3T-1.435*10^-6T^2
n=m/M=155/18=8,61
T1=390°C=663 K
T2=100°C=373

deltaH= n* całka od T1 do T2 z (28,83+13.74*10^-3T-1.435*10^-6T^2)
deltaH=8,61 [28,83*(373-663)+13.74*10^-3*(373^2-663^2)/2-1.435*10^-6*(373^3-663^3)/3]

3. Reakcja 2A+B=3C+D przebiega w fazie gazowej. Gdy zmieszano 1 mol A, 2 mole B i 1 mol D, po ustaleniu się równowagi w temp. 301 k i pod ciśnieniem 2 atm, mieszanina zawierała 0.9 mola C. Oblicz ułamek molowy B w stanie równowagi.

Odpowiedź: 0.4

Wzór:

2A + B = 3C + D

n pocz 1 2 (-) 1

n reaguje -2x -x 3x x

n rowno. 1-2x 2-x 3x 1-x

ul molowe (1-2x)/(4+x) (2-x)/(4+x) 3x/(4+x) (1-x)/(4+x)

n całkowite=(1-2x)+(2-x)+3x+(1-x)= 4+x

podają nam liczność C= 3x=0.9

x=0.3

Xb=(2-x)/(4+x) Przeważnie wchodzi wynik 0.4 :P

4. Opierając się na danych z poniższej tabeli, obliczyć wartość lnKp reakcji 2A(g) + B(g) = 2C(g) w temperaturze 374 K, zakładając niezależność i od temperatury.

Odpowiedź: 6.1

...........So..........delta [H]tw

A(g)... 188 ......... 62.08

B(g) ...205.6........ 0

C(g)... 240.5........33.85

Wzór:

delta S=2C-2*A-B

delta H=2*C-2*A

A= -deltaH + TdeltaS

A=RTlnKp

lnKp=A/(R*T)

Tylko trzeba uważać na jednostki, bo przeważnie S podawane jest w [J/molK] a deltaH w [kJ/mol]!!

5. Związek A ulega rozkładowi termicznemu na B i C w reakcji równoległej o schemacie podanym poniżej. Obie reakcje składowe są nieodwracalnymi reakcjami pierwszego rzędu o stałych szybkości k1 = 0.057 s-1 i k2 = 0.027 s-1. Jakie będzie stężenie B po 12 s jeśli stężenie początkowe A wynosiło 2 mol•dm-3? Wynik podaj w mol•dm-3.

Odpowiedź: 1.8

Schemat reakcji: 2A => 3B oraz 2A => C

6. W reakcji równoległej A rozpada się na 3B (stała szybkości k1 = 0.0383 s-1) i 4C (stała szybkości k2 = 0.046 s-1) w reakcjach pierwszego rzędu. W reaktorze umieszczono czysty substrat A. Po 1462 sekundach stężenie produktu B było równe 0.82 mol•dm-3. Oblicz stężenie produktu C po tym samym czasie. Wynik podaj w mol•dm-3

Odpowiedź:1.3

A=>3B oraz A=>4C

W równaniach 1) dzielimy przez 3; 2) mnożymy przez 4

=>

1)

2)

7. W r-cji 1-szego rzedu Th-->Pa+beta, okres połowicznego rozpadu izotopu Th wynosi 578,4h. Ile było atomów Th na początku jeśli po 100h powstało 202 atomów Pa?

Odpowiedź: 1788.6

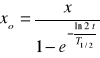
8. Synteza jodowodoru w fazie gazowej: H2 + I2 => 2HI jest reakcją rzędu drugiego (pierwszego rzędu w stosunku do każdego z substratów). Ile razy zmieni się szybkość reakcji (v) w stosunku do jej szybkości początkowej (v0) po przereagowaniu połowy jodu, jeżeli wyjściowa mieszanina zawierała jod oraz wodór w proporcji 1:1.5206? Wynik podać z dokładnością do czterech cyfr dziesiętnych.

Odpowiedź: 0.3

9. Substancja A reaguje dając w dwóch reakcjach równoległych drugiego rzędu o stałych szybkości k1 i k2 dwa produkty B i C. W mieszaninie produktów produkt C stanowi 63.4 %. Obliczyć stosunek stałych szybkości (k1/k2)

Odpowiedź: 0.6

10. Uwzględniając współczynniki aktywności oblicz wartość pH 0.1 molarnego wodnego roztworu amoniaku w temperaturze 298 K wiedząc, że pKb amoniaku wynosi 4,749 a iloczyn jonowy wody w tej temperaturze wynosi 1,008·10-14

Odpowiedź: 12

I

=>

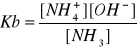
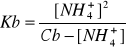
1) pKb=4.749 =>Kb=1.78E-5; Cb=0.1

+ Kb
- KbCb=0

=> liczymy równanie i wybieramy x (zwykle +
)

2)
=
=> pH=-log

II 1)pKw = -logKw

2) pH = pKw - 1/2pKb + 1/2logc

11. W wyniku przebiegu, w stałej temperaturze, reakcji A => ..., stężenie substratu, równe w stanie początkowym 0,1 [mol*dm^-3], zmniejszyło się do połowy po upływie czasu równego 270.87 [s]. Po jakim czasie przereaguje 83% początkowej ilości A, jeżeli reakcja jest rzędu pierwszego? Odpowiedź podać w [s] z dokładnością do dwóch cyfr dziesiętnych.

Odpowiedź: 692.5

12. Czas połówkowy pewnej reakcji opisanej równaniem 2A => B przy stężeniu początkowym substratu A równym 0,02 wynosi 0.6302 s. Wyznaczyć stałą szybkości reakcji przyjmując, że reakcja jest rzędu drugiego. Stałą
szybkości podać w [1/(M*s)] z dokładnością do czterech cyfr dziesiętnych

13. Pewna reakcja przebiega w roztworze jako przeciwbieżna reakcja pierwszego rzędu. Stała szybkości tworzenia produktów k1= 0.000131 s-1. Jeżeli przed rozpoczęciem reakcji znajdował się jedynie substrat A, równowaga ustaliła się na poziomie 81.1 % jego początkowej ilości. Po jakim czasie licząc od momentu rozpoczęcia reakcji powstało 12.2 % B?

Wynik podać w sekundach.

Odpowiedź: 1496

k2/k1 = x/a - x czyli

k2/0.000131=0.189/0.811 z tego liczysz k2

t= -ln/k1 + k2 ( 1 - x(k1 + k2)/k1a)

czyli -ln/k1 + k2 (1 - 0.122 ( k1+k2)/k1)

14. Reakcja 2HI => H2 + I2 jest przeciwbieżną reakcją drugiego rzędu. Dla reakcje tej znaleziono następujące wartości stałej szybkości reakcji rozpadu HI w dwóch temperaturach:
T1=587 K, k1,1=3E-06 mol-1•dm3•s-1, T2=619 K, k1,2=6E-05 mol-1•dm3•s-1.
Obliczyć doświadczalną energię aktywacji. Wynik podać w J/mol.

1)

2)

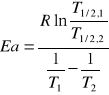
15. Dla reakcji przeciwbieżnej danej równaniem A=2B stałe szybkości tworzenia i rozpadu B wynoszą odpowiednio: k1=0.001 s-1 i k2=0.03 dm3•mol-1•s-1. Obliczyć stężenie równowagowe B jeżeli stężenie wyjściowe A wynosiło 0.96 mol•dm-3. Wynik podaj w mol•dm-3. Odpowiedź podać z dokładnością do trzech cyfr dziesiętnych.
Odpowiedź: 0.085

dcA/dt = k1cA - k2(cB^2)

dx/dt = k1(a-x) - k2(2x)^2

k1(a-x) =k2(2x)^2

4x^2k2 + k1x - k1a=0 => +

25

Zaprojektuj ogniwo bez przenoszenia, w którym będzie przebiegała reakcja
2AgCl = 2Ag + Cl2
Oblicz standardowe SEM tego ogniwa w 298K wiedząc, że standardowe powinowactwo tworzenia AgCl wynosi 108,7 kJ•mol-1.
Odpowiedź: -1.264

2

---