Liczby całkowite

Liczby wymierne

Liczby wymierne różne od
zera

Dodatnie liczby wymierne

Ujemne liczby wymierne

Liczby +1 oraz –1 {+1,-1}

Liczba 0

{0}

półgrup
a

mnożeni
e

dodawani
e

półgrup
a

grupa

grupa

grupa

grupa

grupa

grupa

półgrup
a

półgrup
a

grupa

Przykłady grup

grupa

Liczba 1 {1}

półgrup
a

Funkcje liniowe - działanie jest składaniem

złożone funkcje

y

1

= ax + b

y

2

= c x +

d

a, b, c, d  R

a  0

c 

0

y = a(c x + d ) + b = (a c ) x + ( a d + b
)

działanie, iloczyn określamy w następujący
sposób:

( a x + b )  ( c x + d ) = ( a c ) x + ( ad + b )

I. Sprawdzamy prawo łączności

y

1

= ax + b

y

2

= c x + d

y

3

= e x + f

( a c ) ( e x + f ) + ( a d + b ) = (a c e ) x + ( a c f +
a d + b )
z drugiej strony

( c x + d )  ( e x + f ) = ( c e ) x + ( c f + d )

( a x + b )  [ ( c x + d )  ( e x + f ) ] = a [ ( c

e ) x +

( c f + d ) ] + b = ( a c e ) x + a c f + a d

+ b

c. b. d. o.

II. Sprawdzamy czy istnieje element neutralny

Szukamy funkcji typu: u x + v

( a x + b )  ( u x + v ) = ( a u ) x + a v + b = a

x + b

stąd

a u = a

a v + b = b

więc

u = 1

v = 0

elementem neutralnym jest funkcja:

u x + v = 1 x + 0 = x

c. b. d. o.

( a x + b )  ( a

-1

x + a

-1

b ) = ( a a

-1

) x + a ( - a

-1

b

) + b

= ( a a

-1

) x - ( a a

-1

) b +

b

= x

III. Szukamy elementu odwrotnego

c. b. d. o.

Szukamy funkcji typu: u x + v

stąd

a u = 1

a v + b = 0

więc

u = a

-1

v = - a

-1

b

elementem odwrotnym jest funkcja:

u x + v = a

-1

x - a

-1

b

( a x + b )  ( u x + v ) = ( a u ) x + a v + b = x

Jeżeli w

półgrupie

można wykonać

dzielenie

,

to półgrupa jest

grupą

.

Grupę

( A,f )

nazywamy grupą

przemienną

lub

abelową

jeżeli działanie

f

jest

przemienne

: tzn. dla

dowolnych

elementów a i b grupy A spełniona jest
równość:

f(a,b) = f(b,a)

a f b = b f a

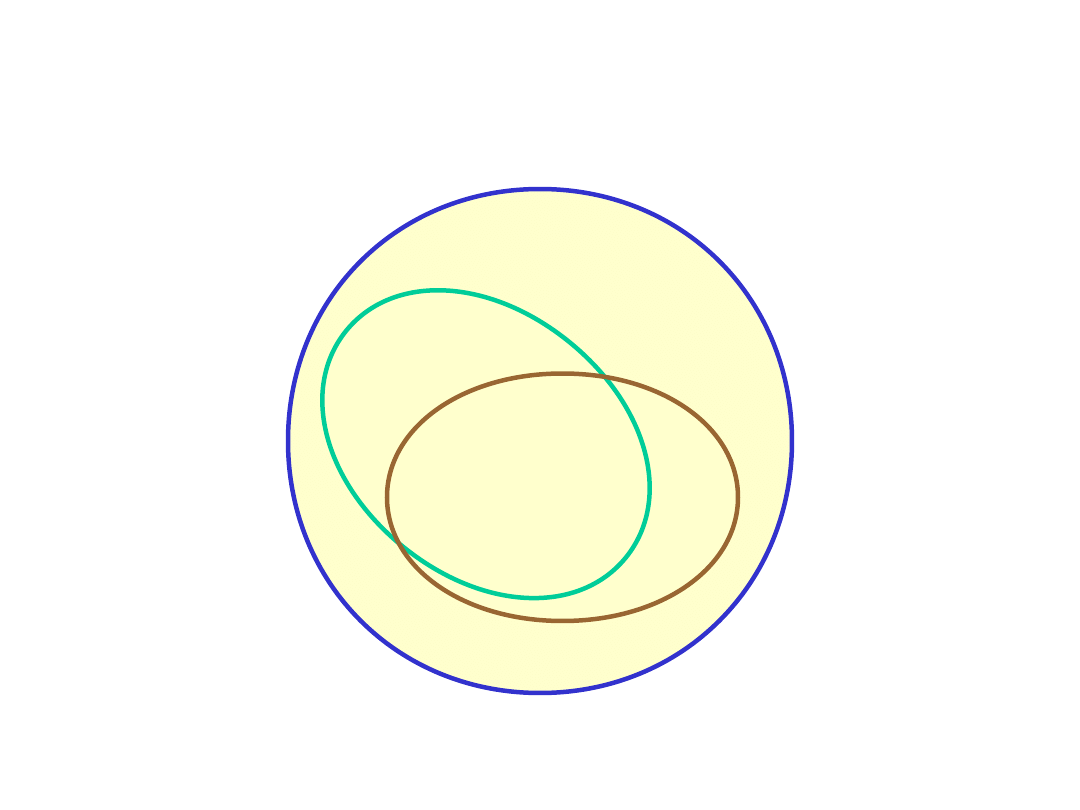
Podgrupy

Grupę

( B; g )

nazywamy

podgrupą

grupy

( A;

f )

jeżeli

B

jest podzbiorem

A

oraz działania

g

i

f

są

takie same.

Podgrupą każdej grupy jest podzbiór składający
się z

elementu jednostkowego. Nosi on nazwę
podgrupy

jednostkowej.

Podgrupą każdej grupy jest sama grupa.

Każda grupa posiada dwie

trywialne podgrupy

.

( A,
f )

B

1

B

2

B

1

, B

2

, B

3

, .........

B

1

 A

B

2

 A

Czy podzbiór B elementów grupy ( A, f )
stanowi podgrupę ?

1. złożenie dowolnej pary elementów
podzbioru B jest elementem zbioru B;
a, b  B  ab  B

2. zbiór B zawiera odwrotności wszystkich
swoich

elementów; a  B  a

-1

 B

Łączność spełniona w B ponieważ B jest
zawarte w zbiorze A.

Należy zbadać, czy :

3. część wspólna zbiorów musi zawierać element
neutralny; e  B

Liczba 1 {1}

Przykłady grup

Liczby całkowite

Liczby wymierne

Liczby wymierne różne od
zera

Dodatnie liczby wymierne

Ujemne liczby wymierne

Liczby +1 oraz –1 {+1,-1}

Liczba 0

{0}

półgrup
a

mnożeni
e

dodawani
e

półgrup
a

grupa

grupa

grupa

grupa

grupa

grupa

półgrup
a

półgrup
a

grupa

grupa

Tablica

półgrup
a

Podgrupę jednostkową i samą grupę nazywamy

podgrupami

niewłaściwymi

: wszystkie

pozostałe

podgrupy nazywamy podgrupami

właściwymi

.

Każda podgrupa podgrupy grupy jest
jednocześnie

podgrupą grupy

A  B

1

 B

2

 B

3

 ..........

Elementy, które znajdują się w każdej z dwóch
lub

więcej podgrup grupy, same tworzą podgrupę
danej

grupy.A

 B

1

 B

2

 B

3

 ..........

Powyższa własność podgrupy umożliwia
znalezienie

najmniejszej podgrupy zawierającej pewne z góry
dane

elementy grupy.

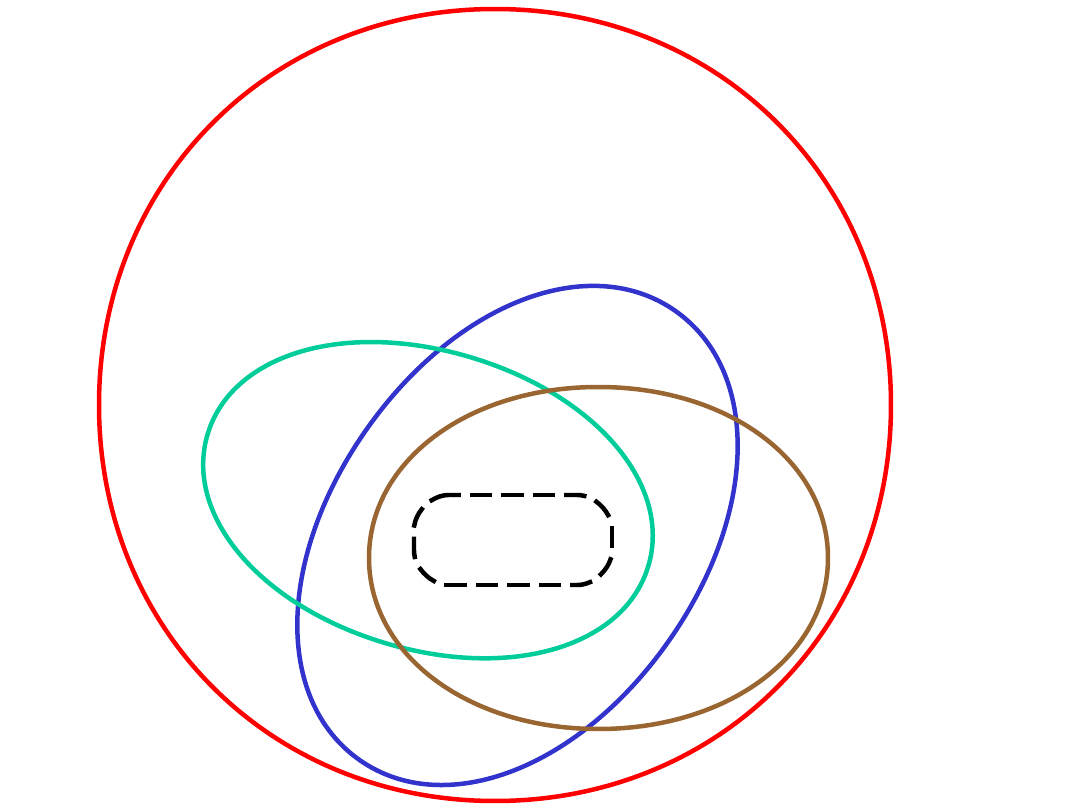
Wspólną część wszystkich podgrup zawierających

elementy a, b, c, ... pewnej grupy nazywamy

podgrupą generowaną przez te elementy i
oznaczamy

ją przez { a, b, c, ....}.

B

2

B

1

B

2

a, b, c, ...

A

Generowanie elementów

Niech

podgrupa {a, b, c, ...}

zawiera

np.. trzy elementy a, b, c tej
podgrupy.

Do tej podgrupy należy też element
jednostkowy.
Na podstawie własności

grupy

należy do niej

zaliczyć wraz z elementami a, b, c każdą ich
potęgę o wykładniku będącym liczbą całkowitą
oraz iloczyn tych potęg:

........

c

b

a

3

2

1

i

i

i

przy czym i

n

są liczbami całkowitymi.

Generatory grup

Podgrupa generowana przez pewne elementy jest

najmniejszą podgrupą, która zawiera każdy z

rozpatrywanych elementów.

Jeżeli podgrupa generowana przez elementy

a, b, c, ... pokrywa się z całą grupą, to
mówimy, że te

elementy tworzą układ generatorów grupy.

Przykłady

1. Grupa generowana przez liczbę 2 w
grupie

addytywnej liczb całkowitych

Grupa składa się z wielokrotności
liczby

2  2•n czyli z liczb parzystych.

2. Podgrupa { 4, 6 } w grupie addytywnej liczb

całkowitych

Elementami podgrupy są liczby w
postaci

4k + 6n gdzie k, n liczby
całkowite.

Są to liczby parzyste gdyż 2 ( 2k + 3n
).

Wszystkie liczby parzyste należą do
grupy

ponieważ 4 • 2 + 6 (-1) = 2

3. Podgrupa { 0 } w grupie addytywnej liczb
całkowitych

4. Podgrupa { 1 } w grupie addytywnej liczb
całkowitych

podgrupa zawiera tylko zero.

Elementami podgrupy są wielokrotności
1•n

czyli wszystkie liczby całkowite.
Podgrupa jest

całą grupą.

Jedynka jest generatorem grupy addytywnej
liczb

Całkowitych.

5. Podgrupa { 1 } w grupie multiplikatywnej liczb
dodatnich

Podgrupa zawiera tylko jedynkę.

Jeśli grupa ma jednoelementowy układ
generatorów,

to grupę tę nazywamy

grupą cykliczną.

Odwzorowania

Jeżeli odwzorowanie f przyporządkowuje różnym

elementom zbioru A różne elementy i każdy
element

zbioru A jest obrazem jakiegoś elementu, to
mówimy, że

f jest odwzorowaniem

wzajemnie

jednoznacznym

lub

bijekcją

.

Relacja jest

wzajemnie jednoznaczna

wtedy i

tylko

wtedy, gdy jest funkcją i gdy relacja do niej
odwrotna

jest także funkcją.

funkc

R

,

R

1

1

R

1











Wzajemnie jednoznaczne odwzorowania zbioru na
siebie

tworzą grupę ze względu na złożenie.

Relacja

R

jest

wzajemnie jednoznaczna

jest

równoważne stwierdzeniu, że relacja jest funkcją

różnowartościową.

1

1

R

1

1

R

1













Własności relacji wzajemnie jednoznacznej

)

yRx

(

)

xRy

(

1

1

R

x

)

R

(

D

y

y

)

R

(

D

x

p

l





















1

1

S

R

1

1

S

,

R













1.

2.

3.

Definicja

Dane są: zbiór A z działaniem  oraz zbór B

z

działaniem  . Odwzorowanie g: A --> B nazywa

się

izomorfizmem

, jeśli:

1.

g

jest wzajemnie jednoznacznym

odwzorowaniem,

czyli

funkcją różnowartościową

bijekcją

2.

)

b

(

g

)

a

(

g

)

b

a

(

g

A

b

,

a











Grupa

( B;f )

jest

izomorficzmym

obrazem grupy

( A;f )

,

gdy istnieje takie wzajemnie jednoznaczne
odwzorowanie

grupy A w B , które zachowuje działanie, czyli:

1. Jeśli a, b są różnymi elementami grupy A, to

g(a) i g(b) są także różnymi elementami

grupy B.
2. Do każdego elementu a’  B można znaleźć

taki

element a  A , dla którego spełniona jest a’ =

g(a).

3. Jeśli a’ = g(a), b’ = g(b) oraz

c = f(a,b), to c’ = f (a’,b’) = g(c)

czyli

g(f(a,b)) = f (g(a),g(b))

Przykłady

1. A = N zbiór liczb naturalnych

B = P zbiór liczb parzystych

odwzorowanie bijekcyjne: g(n) = 2n

g(m+n) = 2 ( m+n ) = 2m + 2n = g(m)
+ g(n)
2. A = R zbiór liczb rzeczywistych z
dodawaniem

B = R

+

zbiór liczb dodatnich z mnożeniem

odwzorowanie bijekcyjne: f: R

+

-->

R

g(x y) = ln(x y) = ln(x) + ln(y) = g(x) +
g(y)

Izomorfizm

Dwie grupy A i B są izomorficzne ( A  B ),

jeżeli

pomiędzy ich elementami można ustalić
wzajemno

jednojednoznaczną odpowiedniość zachowaną
przy

działaniu grupowym.

Warunki

izomorfizmu:

1. Różne elementy mają różne obrazy.

2. Każdy element jest obrazem pewnego
elementu.

3. Zachowane są działania grupowe.

morfizmy

Odwzorowanie spełniające jedynie

warunek 3

-zachowanie działania - nosi nazwę

homomorfizmu

Odwzorowanie

homomorficzne

spełniające

dodatkowo

warunek 1

- różne elementy mają

różne obrazy - nosi nazwę

monomorfizmu

Odwzorowanie

homomorficzne

spełniające

dodatkowo

warunek 2

-każdy element jest

obrazem pewnego elementu - nosi nazwę

epimorfizmu

Istnieją cztery różne przypadki odwzorowań albo

inaczej odwzorowanie

homomorficzne

i jego

trzy

specjalne odmiany:

1.

monomorfizm

warunki: 1,

3

2.

epimorfizm

warunki: 2, 3

3.

izomorfizm

warunki:

1, 2, 3

izomorfizm

warunki:

1, 2, 3

homomorfizm

warunki:

3

monomorfizm

warunki:

1, 3

epimorfizm

warunki:

2, 3

1. Różne elementy mają różne obrazy.

2. Każdy element jest obrazem pewnego
elementu.

3. Zachowane są działania grupowe.

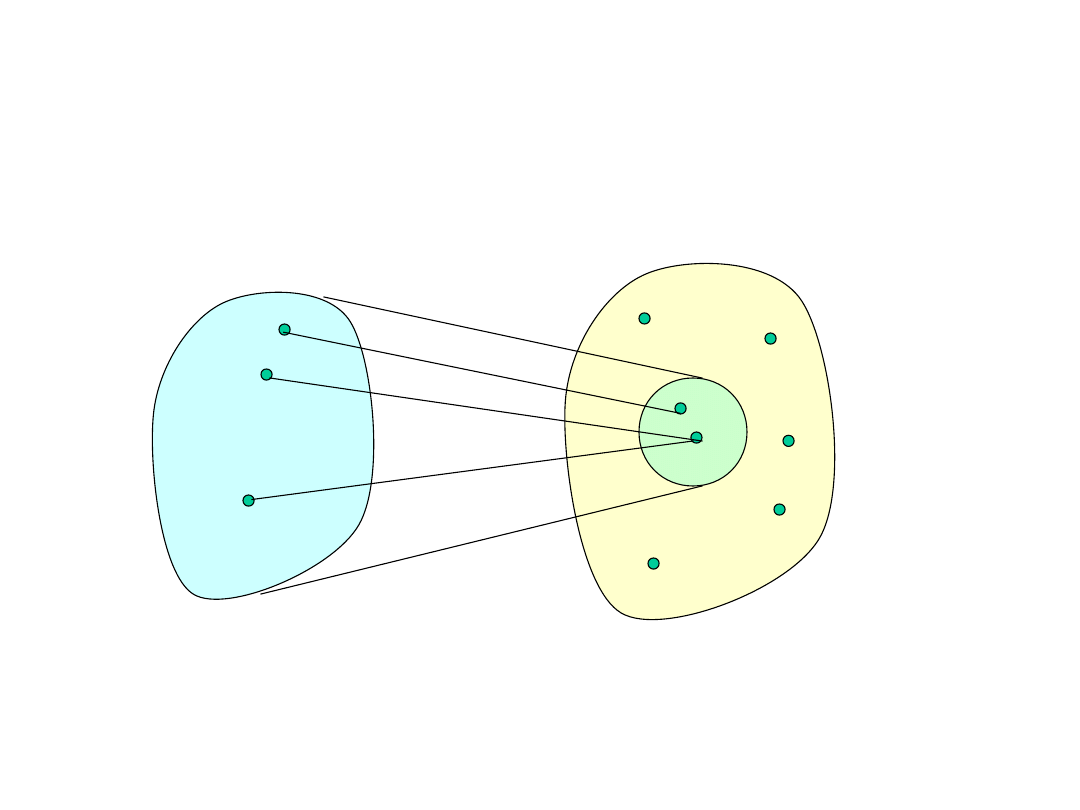
Określenie f: AB oznacza tylko tyle, że

odwzorowujemy elementy A w jakiś sposób w
elementy B

f

A

B

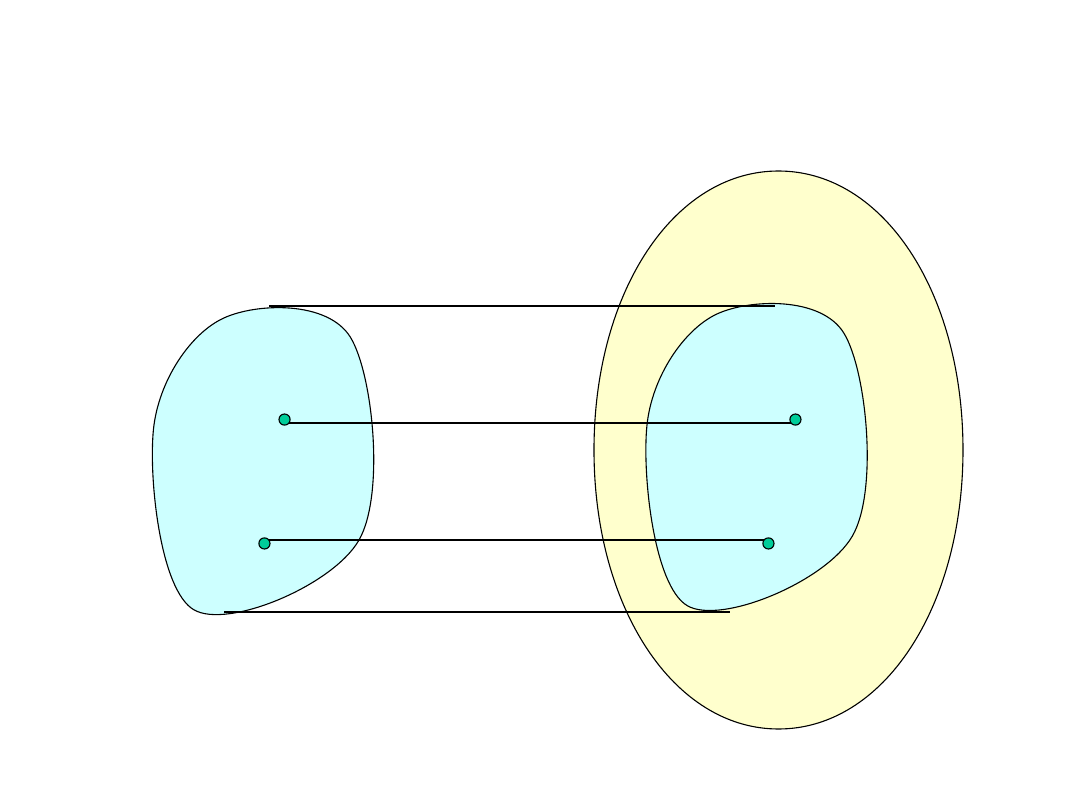
monomorfiz
m

A

B

1. Różne elementy mają różne
obrazy.

3. Zachowane są działania
grupowe.

epimorfizm

A

B

2. Każdy element jest obrazem
pewnego elementu
3. Zachowane są działania
grupowe.

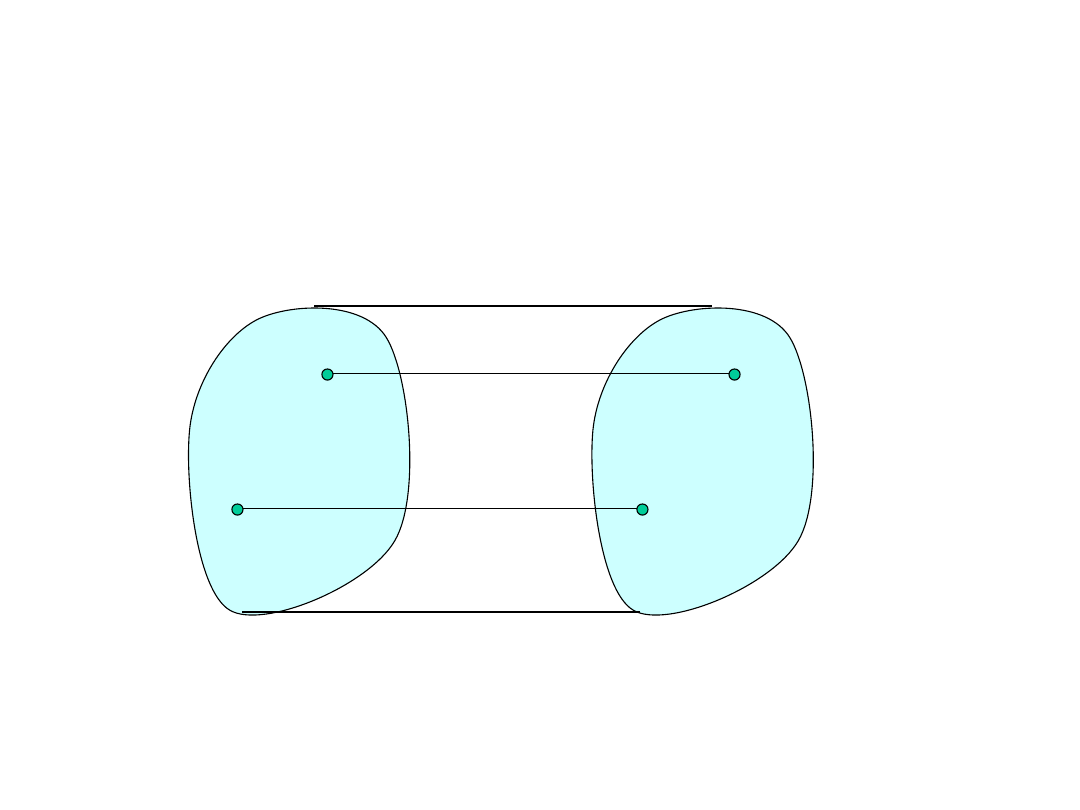
Izomorfizm

A

B

1. Różne elementy mają różne
obrazy.

2. Każdy element jest obrazem
pewnego elementu.

3. Zachowane są działania
grupowe.

Zbiory równoliczne

Zbiory są równoliczne jeżeli mają tę samą ilość
elementów.

A rl

R

B

relacja R stwierdza

równoliczność

zbiorów A

i B.

Warunki równoliczności zbiorów A i B :

1. R  1 - 1

2. D

l

( R ) = A

3. D

p

( R ) = B

Definicja

równoliczności

A rl

R

B  R  1 - 1  [ D

l

( R ) = A ] 

[ D

p

( R ) = B ]

Relacja

równoliczności

jest

zwrotna

,

symetryczna

i

przechodnia

w każdej rodzinie zbiorów:

A rl

R

A

A rl

R

B  B rl

R

A

A rl

R

B  B rl

R

C  A rl

R

C

Relacja

równoliczności

jest relacją

równoważności

w

każdej rodzinie zbiorów:

Równoliczność dwóch zbiorów

A

i

B

można

sprawdzić dwiema metodami:
1. można przeliczyć z osobna obydwa zbiory i
porównać wyniki przeliczeń,
2. polega na utworzeniu par ( a, b ) z elementów

należących do obydwu zbiorów i sprawdzeniu

czy pozostaje któryś z elementów bez pary.

Dwa zbiory są równoliczne gdy istnieje
odwzorowanie wzajemnie jednoznaczne jednego
zbioru w drugi.

Ta druga metoda pozwala na uogólnienie
pojęcia równoliczności na zbiory

nieskończone

.

Przykłady

1. a,b  Z

relacja określona wzorem:

aR

1

b  a = 2b

2. Relacja xR

2

y  x > 0  x + y = 0

stwierdza równoliczność zbiorów {x: x > 0 } i {x:
x < 0 }

Zbiór liczb całkowitych podzielonych
przez 2 oraz zbiór liczb całkowitych są
równoliczne.

Moc zbioru

Każdemu zbiorowi A przyporządkowuje się
pewien

obiekt zwany liczbą kardynalną lub mocą

oznaczany przez

A

Dwóm zbiorom A i B przyporządkowana jest
ta

sama liczba kardynalna wtedy i tylko wtedy,
gdy

zbiory są równoliczne:

)

B

rl

A

(

B

A

R





Niepusty zbiór

A

jest zbiorem

nieskończonym

wtedy i tylko wtedy gdy, zbiory

A

i

A-{a}

są

równoliczne dla dowolnego jego elementu

a

.

Zbiorami

skończonymi

są wszystkie zbiory, które

nie są zbiorami

nieskończonymi

.

Zbiór

nieskończony t

o taki zbiór, który jest

równoliczny z

pewnym swoim właściwym podzbiorem

n

jest liczbą naturalną wtedy i tylko wtedy, gdy

jest mocą

dowolnego zbioru należącego do rodziny zbiorów

skończonych

-

Sk

.

Liczby kardynalne tworzą zbiór. Zmiennymi
będącymi

elementami tego zbioru oznaczamy małymi
literami

alfabetu gotyckiego:

, , , .

Liczby kardynalne, będące mocami zbiorów
nieskończonych nazywamy liczbami

pozaskończonymi.

Moc zbioru wszystkich liczb naturalnych

N

nazywamy mocą

alef zero

i oznaczamy



o

.

Symbol



- alef

jest pierwszą literą alfabetu

hebrajskiego

.



o

= N

Zbiory skończone i zbiory o mocy



o

nazywamy zbiorami

przeliczalnymi

.

Moc zbioru wszystkich liczb rzeczywistych

R

nazywamy mocą

kontinuum

i oznaczamy



.



R





o





Istnieje wiele liczb
pozaskończonych.

Arytmetyka liczb kardynalnych

Suma liczb
kardynalnych
Niech

A

i

B

będą zbiorami rozłącznymi o

mocach

odpowiednio



i



.

Liczbę kardynalną



+



określamy jako moc

zbioru

A

U

B

Iloczyn liczb
kardynalnych
Liczbę kardynalną



•



określamy jako moc

iloczynu

kartezjańskiego zbiorów

A



B

Własności działań na liczbach kardynalnych
nieskończonych różnią się od własności zwykłych
działań arytmetycznych.

Jeżeli



<



to



+



=



oraz



•



=



Relacja R porządkuje zbiór A wtedy i tylko wtedy,
gdy:

Relacja porządkuje pewien zbiór wtedy i tylko
wtedy, gdy

jest

spójna, asymetryczna i przechodnia

.





bRa

aRb

b

a

A

b

,

a















bRa

~

aRb

A

b

,

a











aRc

bRc

aRb

A

b

,

a









A  P(R)

Zbiory uporządkowane

Przykłady

1. Relacja większości lub mniejszości jest
relacją porządkującą

2. Relacje  i  nie porządkują zbiorów N, Z,

W i R, ponieważ nie są w tych zbiorach
asymetryczne.

3. Relacja  nie porządkuje żadnego zbioru o

dwóch co najmniej elementach.

Dowolną relację porządkującą oznaczamy
symbolami

, ’, ’’, ’’’.

Wyrażenie a  b czytamy: element a jest

wcześniejszy od elementu b lub element a
poprzedza element b.

Relacja porządkuje zbiór A gdy dla a, b, c  A

spełnione są warunki:

2. a  b  ( a  b  b  a )

3. a  b  ~( b  a )

4. ( a  b )  ( b  c )  a  c

1. A  P(  )

Para uporządkowana

jest zbiorem uporządkowanym, wtedy i tylko
wtedy, gdy relacja  porządkuje zbiór A .



,

A

Zbiór uporządkowany składa się ze zbioru
nieuporządkowanego oraz umowy
porządkującej elementy tego zbioru

Przykłady par uporządkowanych:









,

R

,

,

W

,

,

C

,

,

N

Element x jest pierwszym elementem
zbioru uporządkowanego



,

A

wtedy i tylko wtedy, gdy:

)

y

x

y

x

(

A

x

A

y

















Zbiór



,

B



,

A

jest podzbiorem
zbioru

wtedy i tylko wtedy, gdy:

A

B 

Zbiór B jest w
zbiorze



,

A

ograniczony od dołu

wtedy i tylko wtedy, gdy:

)

y

x

y

x

(

,

A

B

B

y

A

x























Zbiór uporządkowany jest dobrze
uporządkowany

wtedy i tylko wtedy, gdy każdy jego podzbiór
niepusty

ma element pierwszy.

Relacja R częściowo porządkuje zbiór A wtedy i
tylko

wtedy, gdy A  P(R) i jest w nim asymetryczna i
przechodnia.

Relacja R nie porządkuje lub częściowo
porządkuje zbiór A wtedy i tylko wtedy, gdy
spełnia warunki 1., 3., 4..

2. a  b  ( a  b  b  a )

3. a  b  ~( b  a )

4. ( a  b )  ( b  c )  a  c

1. A  P(  )