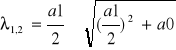
PŁASZCZYZNA FAZOWA

Portret fazowy-jest to taka ilosc trajektorii przy różnych warunkach początkowych, która pozwala określić zachowanie się układu oraz jego stan w każdym (dowolnym) punkcie. Strzałki na trajektoriach wskazują kierunek upływu czasu. Trajektorie nie mogą się przecinać (jednoznaczność ukł. równań. Wyjątek to p osobliwe gdzie nie można wyznaczyć równania trajektorii. Portret fazowy jest jednoznaczny wtedy, gdy rozwiązania równania różniczkowego danego układu są ciągłe względem warunków początkowych i jednoznaczne (przez każdy punkt przechodzi tylko 1 trajektoria z wyjątkiem punktów osobliwych)

Trajektoria fazowa-jest to linia (krzywa) pokazująca stan układu w kolejnych chwilach czasowych (jest to zbiór kolejnych stanów dynamicznych układu w czasie) Z określenia współ. Fazowych wynika , że można im nadać sens „położenia” (x1) i „prędkości”(x2=x1). Zatem wartość zmiennej x1 przy x2>0 powinna wzrastać, przy x2<0 maleć, a przy x2=0 osiągać lokalne ekstremum. Tak więc trajektorie przebiegają w górę półpłaszczyźnie w prawo, w dolnej w lewo, oś x1 mogą przecinać, ale ze styczną prostopadłą do tej osi. Mając dane równanie stanu x1'=x2 i x2'=f(x1,x2) dzieląc otrzymamy dx2/dx1=f(x1x2)x2 - równanie różniczkowe trajektorii którego równanie stanowi rodzina krzywych x2=x2(x1) odpowiadających różnym warunkom początkowym (x10,x20) Trajektoria wychodzi z punktu przedstawiającego warunki początkowe i albo (l) kończy się w punkcie równowagi, albo zdąża do nieskończoności, albo przechodzi w krzywą zamkniętą zwaną cyklem granicznym.

Cykl graniczny - dla układów nieliniowych jest to zjawisko stanowiące trajektorię zamkniętą, obiegającą okresowo punkt równowagi λ₁,λ₂<0 węzeł stabilny, λ₁,λ₂>0 węzeł niestabilny, λ₁,λ₂<0 siodło, Re λ_1,2<0 ognisko stabilne, Re λ_1,2>0 ognisko niestabilne, Re λ_1,2=0 środek.

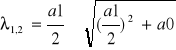
Izokliny - linia dx2/dx1=A=const łączące na płaszczyźnie fazowej punkty o jednakowym nachyleniu krzywych całkowych. Równanie izokliny f(x1,x2)/x2=A zmieniając A otrzymuje się różne izokliny. Równanie izokliny powstaje z równania
przez podstawienie

, a więc
Jest to równanie algebraiczne łatwe do rozwiązania lub wykreślenia. Wartość stałej C określa nachylenie (tg kąta) pod jakim trajektorie przecinają izoklinę. Przyjęcie kilku wartości C daje rodzinę izoklin, te zaś z kolei pozwalają w przybliżeniu naszkicować kształt trajektorii.

Płaszczyzna fazowa -jest to przestrzeń stanów w zasadzie dla układów drugiego rzędu, gdzie mamy tylko dwie współrzędne stanu (współ.fazowe) Zalety tej płaszczyzny ujawniają się zwłaszcza przy badaniu układów nieliniowych. Istota pł.fazowej polega na tym, że na podstawie kształtu wykresu (trajektorii) można określić właściwości układu dynamicznego, tj. wł. Statyczne, dynamiczne, stabilność. Na pł.fazowej rysuje się trajektorię fazową. Osiami pł.fazowej są y i y'. Kierunek przesuwania się punktu po krzywej całkowej jest zgodny z kierunkiem ruchu wskazówek zegara.

Punkt osobliwy - jest to punkt równowagi układu Z!'=X2'=0 - warunek stanu ustalonego. Punktem osobliwym prawie zawsze jest początek układu współrzędnych x1=x2=0. Punkty osobliwe mogą leżeć tylko na osi x1 (gdyż x1'=x2=0)

UKŁADY DYNAMICZNE

Licznik - jest to urządzenie do zliczania impulsów elektrycznych (mogą zarówno dodawać jak i odejmować w zależności od wartości sygnałów). Układem dynamicznym nazywamy dowolny układ fizyczny rozpatrywany z punktu widzenia zachodzących w nim procesów dynamicznych.(przedstawianych za pomocą liniowych równań różniczkowych zwyczajnych o stałych parametrach) Ściśle wchodzą zależności pomiędzy przebiegami czasowymi zmiennych, a nie ich wartości chwilowych.

Stan układu -jest to zbiór wielkości dostarczających taką ilość informacji, które wystarczają do oceny zachowania się obiektu w przyszłości, czyli do jednoznacznego określenia zachowania się układu.

Dynamiczny układ liniowy i stacjonarny może być opisany przez n równań różniczkowych I-go rzędu.

x(t)=Ax(t)+Bu(t)

y(t)=Cx(t)+Du(t)

Sterowalność oznacza możliwość osiągnięcia dowolnego stanu układu w skończonym czasie za pomocą dopuszczalnego sterowania.

Dopuszczalne sterowanie-jest to sterowanie ograniczone przedziałami i ciągłe.

Warunkiem koniecznym i dostatecznym sterowalności jest, aby macierz S=[B,AB,A²B,...,A^n-1B] o n wierszach i m kolumnach była rzędu n ,czyli aby miała n liniowo niezależnych kolumn.

Obserwowalność oznacza , że na podstawie przebiegu sygnału wyjściowego w skończonym przedziale czasu można określić stan układu w tym przedziale. Warunkiem koniecznym i dostatecznym obserwowalności jest, aby macierz

C

AC

O= A²C

C...)

A^N-1C o wymiarach n*n była rzędu n , czyli zawierała n-liniowo niezależnych wierszy.

Ocena sterowalności i obserwowalności może być przeprowadzona na podstawie analizy:

• postaci kanonicznej równania stanu i równania wyjścia;

• bezpośredniej analizy schematu blokowego,

Układ jest stabilny ,gdyż dla stałej skończonej wartości zakłócenia i dla dowolnego stanu początkowego.

Sygnał wyjściowy będzie dążył do skończonej wartości ustalonej.

Układ jest sterowalny - jeżeli dla każdego t₀ istnieje takie sterowanie x(t), które spowoduje w skończonym przedziale czasu (t_k-t₀) przejście układu z dowolnego stanu początkowego u(t₀)=U₀ do stanu końcowego u(t_k)=U_k=0

Układ jest obserwowalny - w przedziale czasu t₀<t<t_k jeżeli na podstawie znajomości wejść (sterowań) x(t) i wektora wyjść y(t) w tym przedziale można wyznaczyć wektor stanu U₀ układu w chwili t₀. Warunkiem koniecznym i dostatecznym obserwowalności jest aby podany rząd macierzy był równy (n) wymiarowy wektora stanu.

Układ jest stabilny - gdy części rzeczywiste pierwiastków równania charakterystycznego są ujemne N(s)=s^2+s+1 S(1,2)= -0,5+/-j~3/2 Re(S12)=-0,5 Zamknięty układ liniowy jest stabilny, gdy dla stałej skończonej wartości zakłócenia i dla dowolnego stanu początkowego sygnał wyjściowy będzie dążył do skończonej wartości ustalonej. Lokalne - po przekroczeniu granicy x1 x2 układ się wróci do stanu poprzedniego i jest niestabilny. Będzie lokalnie jeżeli dla każdego dowolnie małego obszaru e można dobrać taki obszar r₀ stanów początkowych, że cała trajektoria stanu układu x(t) dla warunków początkowych zwartych w obszarze r₀ będzie zawarta także w obszarze e.

Globalnie - (o równaniu X'=Ax) wtedy i tylko wtedy gdy wszystkie wartości własne macierzy A mają niedodatnie części rzeczywiste i każda wartość własna o zerowej części rzeczywistej jest pierwiastkiem jednorodnym wielomianu. Stabilność punktu równowagi przy dowolnie dużych warunkach początkowych nazywa się globalną.

Asymptotyczna - jeżeli wektor stanu powróci do stanu równowagi.

Kryteria stabilności - analityczne (Hurwitza, Roughta) graficzne (Nequista) anal-graf (Michajłowa)

Stabilność lokalną rozumiemy stabilność tylko w punkcie równowagi bez określenia zakresu sygnałów zaburzających, po ustąpieniu których układ wraca do równowagi. Mówiąc o stabilności globalnej określamy jednocześnie obszar sygnałów zaburzających, po przejściu których układ zachowuje swój pierwotny stan równowagi. Jeżeli obszar stabilności globalnej obejmuje wszystkie możliwe sygnały wejściowe - totalna

Wartość A22 elementu macierzy A ma wpływ na tłumienie amplitudy odpowiedzi A12 na częstość oscylacji A11 zwiększa amplitudę odpowiedzi. Macierz A obrazuje wszystkie połączenia „skrośne” pomiędzy poszczególnymi zmiennymi stanami na wejściach integratorów. B,C i D wyraża połączenia typu „każdy z każdym” odpowiednich zmiennych. A-n*n - macierz procesu , stanu, stanu (układu)B-n*r - wymuszenia (wejścia, sterowania) C-m*n - odpowiedzi (wyjścia) D-m*r - transmisyjna u(t) - wektor wymuszenia , x(t) - wektora stanu x(t) y(t) - wektor odpowiedzi.

Układ sterowalny - jest to taki układ, który stosując ograniczone przedziałem ciągłe sterowanie można przeprowadzić z dowolnie zadanego stanu początkowego do początku układu współrzędnych w skończonym czasie.

Układ jest obserwowalny wtedy, gdy przy dowolnie zadanym sterowaniu istnieje skończony przedział czasu, taki, że na podstawie znajomości sterowania i odpowiedzi w tym przedziale można wyznaczyć stan początkowy tego układu.

Rodzaje członów: bezinercyjny , całkujący, intercyjny , różniczkujący, różniczkujący-rzeczywisty, proporcjonalno-całkujący , dwuintercyjny.

Uchyb w regulacji ciągłej dąży do zera i jeśli nie ma zakłóceń jest zawsze wartością dodatnią, a w regulacji dwupołożeniowej uchyb oscyluje w pewnych granicach wartością zmiennej i jest dodatni i ujemny.

Uchyb jest to różnica między sygnałem zadanym, a regulowanym.

czas regulacji

uchyb statyczny

Porównać pojęcia uchybu w regulacji ciągłej i dwupołożeniowej.

Uchybem w regulacji ciągłej nazywamy różnicę między wartością zadaną
a nielinjością mierzoną Y. E(epsylon)=
Uchyb podczas regulacji zmienia się w czasie. Uchyb w regulacji ciągłej jest zawsze dodatni (chyba, że zakłócenia) i zawsze dąży do zera.

Uchyb w regulacji dwupołożeniowej definiujemy jako różnicę między wartością zadaną
, a mierzoną
. W odróżnieniu od uchybu w regulacji ciągłej, w regulacji dwupołożeniowej uchyb zmienia znak. Jest raz dodatni, raz ujemny. Bardzo rzadko jest zbliżony lub równy zero.

Wyjaśnić jaki jest wpływ wartości wymuszenia regulatora dwupołożeniowego na przebieg regulacji?

Regulator tak steruje sygnałem regulowanym, że wielkość regulowana oscyluje wokół wartości zadanej. Oscylacje te odbywają się z pewną częstotliwością i amplitudą. Jeśli wartość wymuszenia jest niska to średnia wartość na jakiej układa się oscylacja będzie większa niż wartość zadana. Jeśli wymuszenie
będzie na średnim poziomie to wartość średnia wokół której oscyluje wielkość regulowana będzie równe wartości zadanej. Gdy natomiast wymuszenie będzie bliskie poziomu K to średnia wartość wokół której oscyluje wielkość regulowana będzie niższa niż wartość zadana.

Podać i wyjaśnić terię jakości regulacji ciągłej.

Wskaźniki dotyczące cech odpowiedzi skokowej.

• czas regulacji
  -to czas liczony od chwili przyłożenia wymuszenia do chwili po której odchylenie regulacji jest stale mniejsze od dopuszczalnych granic =
  

odchylenie max
(kappa)-im silniej są tłumione przebiegi oscylacyjne , tym mniejsza jest wartość
(kappa).Przeregulowanie rośnie w miarę zbliżania się do granicy stabilności.

• aperiodyczność - przebiegi przejściowe aperiodyczne charakteryzują się błędem oscylacji Można traktować je jako

przypadek szczególny, gdy

• pasmo przenoszenia, zakres częstotliwości w którym wartości stosunku amplitud wyjścia do wejścia oraz przesunięcia fazowego między wyjściem a wejściem utrzymane są w żądanych granicach

• wskaźniki regulacji

Wyjaśnić jaki jest wpływ wartości wymuszenia regulatora dwupołożeniowego na przebieg regulacji.

Regulator tak steruje sygnałem regulowanym , że wielkość regulowana oscyluje wokół wartości zadanej . Oscylacje te odbywają się z pewną częstotliwością i amplitudą .Jeśli wartość wymuszenia jest niska to średnia wartość na jakiej ustala się oscylacja będzie większa niż wartość zadana. Jeśli wymuszenie x₀ będzie na średnim poziomie to wartość średnia ,wokół której oscyluje wielkość regulowana będzie równa wartości zadanej. Gdy natomiast wymuszenie będzie bliskie poziomu k to średnia wartość ,wokół której oscyluje wielkość regulowana będzie niższa niż wartość zadana.

Porównać pojęcia uchybu w regulacji ciągłej i dwupołożeniowej.

Uchybem w regulacji ciągłej nazywamy różnicę między wartością zadaną
a nielinjością mierzoną Y. E(epsylon)=
Uchyb podczas regulacji zmienia się w czasie. Uchyb w regulacji ciągłej jest zawsze dodatni (chyba, że zakłócenia) i zawsze dąży do zera.

Uchyb w regulacji dwupołożeniowej definiujemy jako różnicę między wartością zadaną
, a mierzoną
. W odróżnieniu od uchybu w regulacji ciągłej, w regulacji dwupołożeniowej uchyb zmienia znak. Jest raz dodatni, raz ujemny. Bardzo rzadko jest zbliżony lub równy zero

Uchyb w regulacji ciągłej dąży do zera i jeśli nie ma zakłóceń jest zawsze wartością dodatnią, a w regulacji dwupołożeniowej uchyb oscyluje w pewnych granicach wartością zmiennej i jest dodatni i ujemny.

Uchyb jest to różnica między sygnałem zadanym, a regulowanym.

Podać i wyjaśnić terię jakości regulacji ciągłej.

Wskaźniki dotyczące cech odpowiedzi skokowej.

• czas regulacji
  -to czas liczony od chwili przyłożenia wymuszenia do chwili po której odchylenie regulacji jest stale mniejsze od dopuszczalnych granic =
  

odchylenie max
(kappa)-im silniej są tłumione przebiegi oscylacyjne , tym mniejsza jest wartość
(kappa).Przeregulowanie rośnie w miarę zbliżania się do granicy stabilności.

• aperiodyczność - przebiegi przejściowe aperiodyczne charakteryzują się błędem oscylacji Można traktować je jako

przypadek szczególny, gdy

• pasmo przenoszenia, zakres częstotliwości w którym wartości stosunku amplitud wyjścia do wejścia oraz przesunięcia fazowego między wyjściem a wejściem utrzymane są w żądanych granicach

• wskaźniki regulacji

Podać i wyjaśnić kryteria jakości regulacji ciągłej.

Wskaźnik dotyczącej cech odpowiedzi skokowej:

• czas regulacji t_r - t_o czas liczony od chwili przyłożenia wymuszenia , do chwili po której odchylenie regulacji jest stałe mniejsze od dopuszczalnych granic
  

• odchylenie maksymalne χ - im silniej są tłumione przebiegi oscylacyjne , tym mniejsze jest wartość χ . Przeregulowanie rośnie w miarę zbliżenia się do granicy stabilności.

• Aperiodyczność - przebiegi przejściowe aperiodyczne charakteryzują się błędem oscylacji. Można traktować je jako przypadek gdy χ =0%.

• Pasmo przenoszenia zakres częstotliwości, w którym wartości stosunku amplitud wyjścia do wejścia oraz przesunięcia fazowego między wyjściem a wejściem utrzymane są w żądanych granicach .

Wskaźnik regulacji.

Uzasadnić wpływ wartości wymuszenia skokowego na odpowiedź układu różniczkującego rzeczywistego, podać jego tansmintancję.

Odpowiedź na wymuszenie skokowe wyznaczamy z transmintancji.

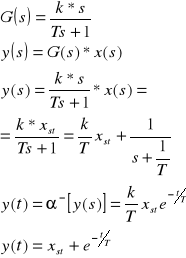
Zależność wartości wymuszenia skokowego i odpowiedzi jest liniowa , gdyż wymuszenia jest wprost proporcjonalne do odpowiedzi . Im większe wymuszenie tym większy spadek wartości odpowiedzi w jednostce czasu.

Y X

x_st

y(s)

T

T

Licznik - jest to urządzenie do zliczania impulsów elektrycznych (mogą zarówno dodawać jak i odejmować w zależności od wartości sygnałów). Układem dynamicznym nazywamy dowolny układ fizyczny rozpatrywany z punktu widzenia zachodzących w nim procesów dynamicznych.(przedstawianych za pomocą liniowych równań różniczkowych zwyczajnych o stałych parametrach) Ściśle wchodzą zależności pomiędzy przebiegami czasowymi zmiennych, a nie ich wartości chwilowych.

Stan układu -jest to zbiór wielkości dostarczających taką ilość informacji, które wystarczają do oceny zachowania się obiektu w przyszłości, czyli do jednoznacznego określenia zachowania się układu.

Dynamiczny układ liniowy i stacjonarny może być opisany przez n równań różniczkowych I-go rzędu.

x(t)=Ax(t)+Bu(t)

y(t)=Cx(t)+Du(t)

Sterowalność oznacza możliwość osiągnięcia dowolnego stanu układu w skończonym czasie za pomocą dopuszczalnego sterowania.

Dopuszczalne sterowanie-jest to sterowanie ograniczone przedziałami i ciągłe.

Warunkiem koniecznym i dostatecznym sterowalności jest, aby macierz S=[B,AB,A²B,...,A^n-1B] o n wierszach i m kolumnach była rzędu n ,czyli aby miała n liniowo niezależnych kolumn.

Obserwowalność oznacza , że na podstawie przebiegu sygnału wyjściowego w skończonym przedziale czasu można określić stan układu w tym przedziale. Warunkiem koniecznym i dostatecznym obserwowalności jest, aby macierz

C

AC

O= A²C

C...)

A^N-1C o wymiarach n*n była rzędu n , czyli zawierała n-liniowo niezależnych wierszy.

Ocena sterowalności i obserwowalności może być przeprowadzona na podstawie analizy:

• postaci kanonicznej równania stanu i równania wyjścia;

• bezpośredniej analizy schematu blokowego,

Układ jest stabilny ,gdyż dla stałej skończonej wartości zakłócenia i dla dowolnego stanu początkowego.

Sygnał wyjściowy będzie dążył do skończonej wartości ustalonej.

Układ jest sterowalny - jeżeli dla każdego t₀ istnieje takie sterowanie x(t), które spowoduje w skończonym przedziale czasu (t_k-t₀) przejście układu z dowolnego stanu początkowego u(t₀)=U₀ do stanu końcowego u(t_k)=U_k=0

Układ jest obserwowalny - w przedziale czasu t₀<t<t_k jeżeli na podstawie znajomości wejść (sterowań) x(t) i wektora wyjść y(t) w tym przedziale można wyznaczyć wektor stanu U₀ układu w chwili t₀. Warunkiem koniecznym i dostatecznym obserwowalności jest aby podany rząd macierzy był równy (n) wymiarowy wektora stanu.

Układ jest stabilny - gdy części rzeczywiste pierwiastków równania charakterystycznego są ujemne N(s)=s^2+s+1 S(1,2)= -0,5+/-j~3/2 Re(S12)=-0,5 Zamknięty układ liniowy jest stabilny, gdy dla stałej skończonej wartości zakłócenia i dla dowolnego stanu początkowego sygnał wyjściowy będzie dążył do skończonej wartości ustalonej. Lokalne - po przekroczeniu granicy x1 x2 układ się wróci do stanu poprzedniego i jest niestabilny. Będzie lokalnie jeżeli dla każdego dowolnie małego obszaru e można dobrać taki obszar r₀ stanów początkowych, że cała trajektoria stanu układu x(t) dla warunków początkowych zwartych w obszarze r₀ będzie zawarta także w obszarze e.

Globalnie - (o równaniu X'=Ax) wtedy i tylko wtedy gdy wszystkie wartości własne macierzy A mają niedodatnie części rzeczywiste i każda wartość własna o zerowej części rzeczywistej jest pierwiastkiem jednorodnym wielomianu. Stabilność punktu równowagi przy dowolnie dużych warunkach początkowych nazywa się globalną.

Asymptotyczna - jeżeli wektor stanu powróci do stanu równowagi.

Kryteria stabilności - analityczne (Hurwitza, Roughta) graficzne (Nequista) anal-graf (Michajłowa)

Stabilność lokalną rozumiemy stabilność tylko w punkcie równowagi bez określenia zakresu sygnałów zaburzających, po ustąpieniu których układ wraca do równowagi. Mówiąc o stabilności globalnej określamy jednocześnie obszar sygnałów zaburzających, po przejściu których układ zachowuje swój pierwotny stan równowagi. Jeżeli obszar stabilności globalnej obejmuje wszystkie możliwe sygnały wejściowe - totalna

Wartość A22 elementu macierzy A ma wpływ na tłumienie amplitudy odpowiedzi A12 na częstość oscylacji A11 zwiększa amplitudę odpowiedzi. Macierz A obrazuje wszystkie połączenia „skrośne” pomiędzy poszczególnymi zmiennymi stanami na wejściach integratorów. B,C i D wyraża połączenia typu „każdy z każdym” odpowiednich zmiennych. A-n*n - macierz procesu , stanu, stanu (układu)B-n*r - wymuszenia (wejścia, sterowania) C-m*n - odpowiedzi (wyjścia) D-m*r - transmisyjna u(t) - wektor wymuszenia , x(t) - wektora stanu x(t) y(t) - wektor odpowiedzi.

---