Charakterystyki częstotliwościowe otrzymuje się na podstawie transmitancji widmowej, jeśli ca potraktuje się jako zmienną niezależną, przybierającą wartości od O do + oo. Charakterystyki częstotliwościowe mają nie tylko sens pojęciowy, lecz i pomiarowy* ponieważ wprowadzając eksperymentalnie do układu wymuszenie harmoniczne o nastawianej pulsacji ω = 2πf można mierzyć charakterystyki częstotliwościowe na wyjściu układu. Można rozróżnić następujące charakterystyki częstotliwościoe:

- charakterystykę amplitudową A(ω) =|G(jω)|,

- charakterystykę fazową
ϕ(ω)= arg G(jω),

- charakterystykę raeczywistą R(ω) = Re [G(jω)],

- charakterystykę urojoną Q(ω) = Im [G(jω)]. Dwie ostatnie przedstawiane są w postaci graficznej jako charakterystykę amplitudowo-fazową (wykres Nyquista). To jest krzywą G(j o), którą można otrzymać na płaszczyźnie zmiennej zespolonej o osiach R(co) i Q(o»), po przez uzmiennienie ω.

InterpretacJe charakterystyk:

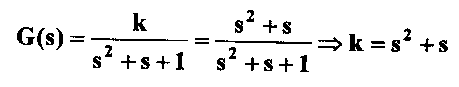
3. Układem nieliniowym - jest każdy układ zawierający chociaż l element nieliniowy. Na przykład, nieliniowe są wszystkie układy zawierające elementy o działaniu przekaźnikowym lub elementy, w których uwzględnimy takie zjawiska jak tarcie suche, luzy, histereza albo mechaniczne ograniczenia ruchu. Elementy i układy nieliniowe opisujemy za pomocą nieliniowych równań różniczkowych .różnicowych lub algebraicznych. Nie obowiązuje ich zasada superpozycji.

Układ statyczny nieliniowy R₁+R₂(i)*i=u

Układ dynamiczny nieliniowy L*di(t)/dt + R(t)*i(t)=u(t)

gdzie : R₂ - oporność zależna nieliniowo od prądu

R(t)=r*e_-^t -współczynnik zależny nieliniowo od czasu.

Podstawową zależnością charakteryzującą nieliniowy układ dynamiczny jest jego charakterystyka statyczna, czyli zależność między jego sygnałem wyjściowym, a sygnałem wejściowym w stanach ustalonych, tj. przy założeniu, że wszystkie pochodne względem czasu sygnałów i współrzędnych układu są równe zeru. Charakterystyka statyczna stanowi zbiór punktów równowagi układu.

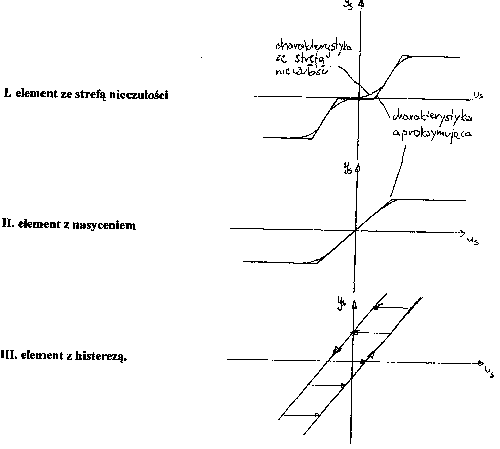
Przykłady:

---