ROZKŁAD ZERO-JEDYNKOWY

xi	0	1
pi	q	p

Parametry rozkładu zero-jedynkowego

,

Dystrybuanta rozkładu zero-jedynkowego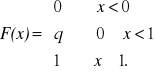

ROZKŁAD DWUMIANOWY

Wykonujemy wielokrotnie takie samo doświadczenie losowe, którego rezultatem może każdorazowo być sukces, z prawdopodobieństwem p, lub porażka, z prawdopodobieństwem q=1-p. Zakładamy, że wyniki pojedynczych doświadczeń są od siebie wzajemnie niezależne. Rozkład liczby odniesionych sukcesów w n wykonanych doświadczeniach nazywa się rozkładem dwumianowym (Bernoulliego).

Jeśli zmienna losowa X oznaczać będzie liczbę sukcesów odniesionych wśród n przeprowadzonych niezależnych doświadczeń losowych, to prawdopodobieństwo odniesienia dokładnie k sukcesów, czyli prawdopodobieństwo przyjęcia przez zmienną X wartości k, jest równe:

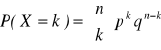
, k=0,1,...,n,

gdzie
oznacza symbol Newtona,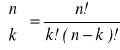
.

Parametry rozkładu dwumianowego

E(X)=np,

.

Wartość oczekiwaną interpretować będziemy jako spodziewaną przeciętną liczbę sukcesów wśród n doświadczeń.

Zadania:

1. Strzelec strzela do tarczy. Prawdopodobieństwo trafienia wynosi 0,2. Niech X będzie zmienną losową przyjmującą wartość 0 w przypadku strzału chybionego i 1 w przypadku trafionego.

1. Jaki jest rozkład tej zmiennej?

2. Oblicz wartość oczekiwaną i wariancję zmiennej X i podaj postać jej dystrybuanty.

2. Oblicz wartości funkcji prawdopodobieństwa rozkładu dwumianowego z parametrami n=4, p=0,3. Oblicz wartość oczekiwaną i odchylenie standardowe w tym rozkładzie. Przedstaw graficznie funkcję prawdopodobieństwa.

3. Rzucamy dwukrotnie monetą. Niech X oznacza liczbę orłów, które wyrzucimy w owych dwóch losowaniach. Podaj rozkład zmiennej X i jej dystrybuantę.

4. Jaki jest rozkład liczby orłów wyrzuconych w 100 rzutach rzetelną monetą. Obliczyć wartość oczekiwaną i odchylenie standardowe.

5. Rzucamy 5 razy sześcienną kostką do gry. Jakie jest prawdopodobieństwo, że dokładnie 3 razy wyrzucimy szóstkę?

Odp.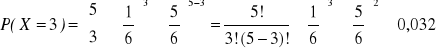
.

(w przybliżeniu średnio w zaledwie trzech przypadkach na 100 będziemy wśród pięciu rzutów trzy razy trafiać na kostce szóstkę)

6. Zawodnik strzela do tarczy 5 razy. Prawdopodobieństwo trafienia wynosi 0,8. Jaki jest rozkład i wartość oczekiwaną liczby trafień. Jakie jest prawdopodobieństwo, że trafi dokładnie 4 razy do tarczy.

ROZKŁADY ZMIENNEJ LOSOWEJ SKOKOWEJ dr Rumiana Górska

- 1 -

---