1

INFORMACJA!

• Udostępniane materiały pomocnicze do nauki 

przedmiotu Wytrzymałość Materiałów są 

przeznaczone w pierwszym rzędzie dla wykładowców. 

Dla właściwego ich wykorzystania konieczny jest 

komentarz osoby rozumiejącej treści zawarte w 

prezentacjach.

• Dla studentów jest to tylko materiał uzupełniający do 

studiów w bezpośrednim kontakcie z prowadzącymi, 

a także ułatwiający zrozumienie treści podręczników.

• Przedstawiana wersja jest pierwszą edycją wykładów 

przeprowadzonych w roku ak. 2009/10 i wymagać 

może  poprawek i uzupełnień. Pobierający te 

materiały proszeni są o przesyłanie swoich uwag na 

adres e-mailowy autora: mc@limba.wil.pk.edu.pl. 

 

 

2

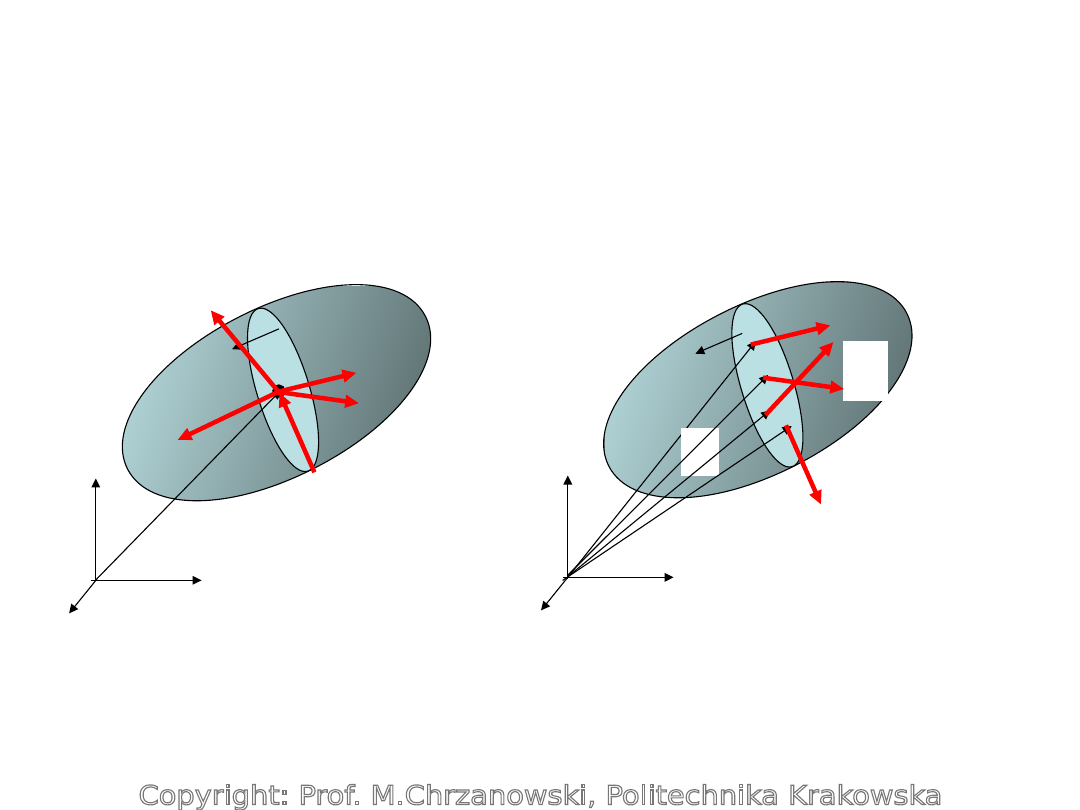
ROZKŁAD  NAPRĘŻEŃ 

 

 

3

Rozkład przestrzenny 
naprężeń

 

n

r

p

p









,







 

r

p

n

n

r

p

p

const





















;





 

n

p

n

r

r

p

p

const





















;

Stan naprężenia

Rozkład  naprężeń

Wektor 
naprężenia

const

n

r

p



const

r

n



n



r

 

 

4

x

2

x

1

x

3

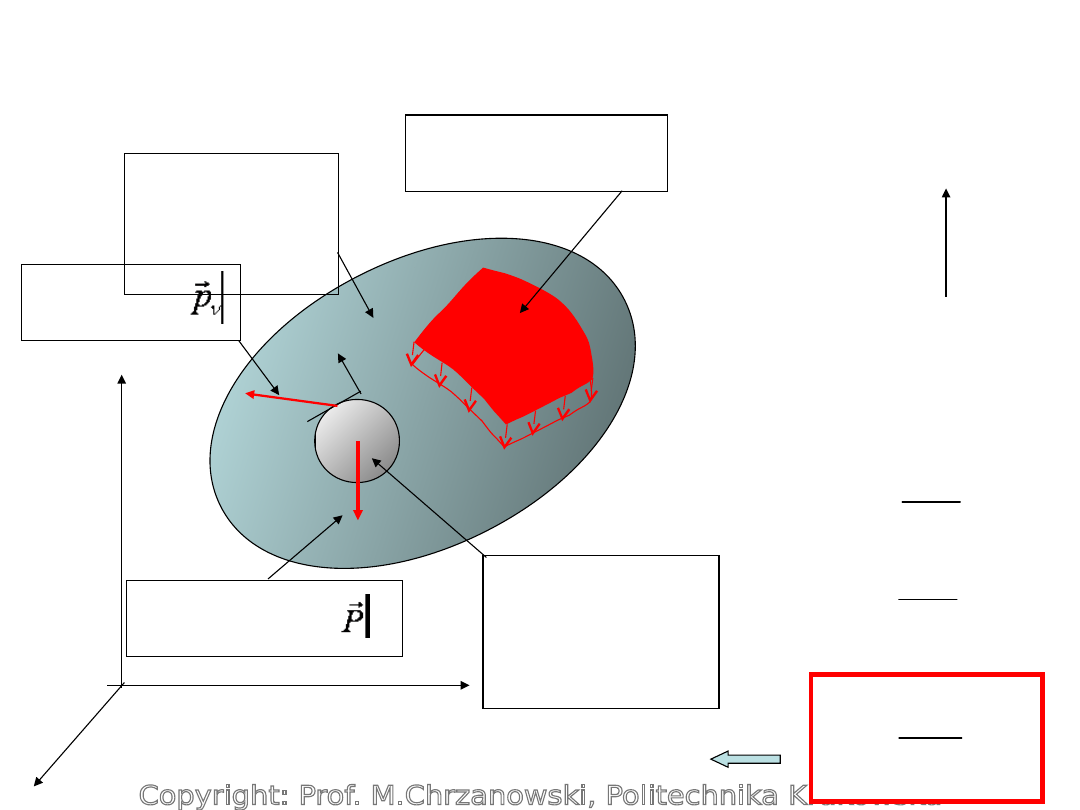
Rozkład przestrzenny 
naprężeń





Objętość 

V

Powierzchnia

 

S

 

i

p









 

i

q

q







Objętość 

V

0

Powierzchnia

 

S

0

Wektor 
naprężenia

Wektor sił 
objętościowych

 

i

P

P



dS

p

dV

P

S

V













0

0

0











0

0

0









dS

dV

P

j

S

ij

V

i







0

0

0









dS

dV

P

S

i

V

i





0

0

0













dV

x

dV

P

V

j

ij

V

i



0

0

























dV

x

P

V

j

ij

i



j

ij

i













0























j

ij

i

x

P







,

,

,

3

2

1

x

x

x

ij

ij







Tw. Greena-Gaussa-
Ostrogradzkiego

Obciążenie 
powierzchniowe



q

 

 

5

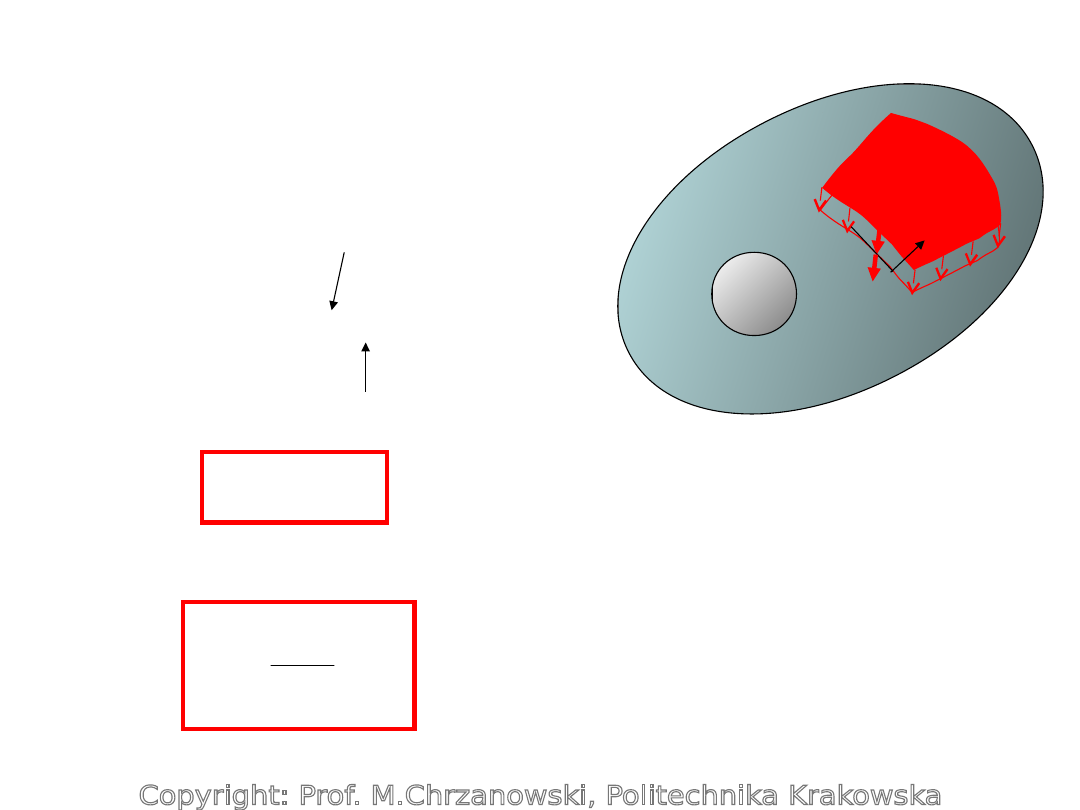
Rozkład przestrzenny 
naprężeń

0























j

ij

i

x

P







Na powierzchni ciała 
wektor naprężenia jest 
znany:



q



p



j

ij

i

i

q

















Naprężenia na powierzchni 
ciała

Współrzędne wersora normalnego do 
powierzchni

j

ij

i

q











Są to 

statyczne warunki brzegowe

, które musi spełniać rozwiązanie 

równania:

Równanie to (równanie Naviera) nosi 
nazwę równania równowagi 
wewnętrznej.

 

 

6

Rozkład przestrzenny 
naprężeń

0























j

ij

i

x

P



Jest to układ 3 rownań różniczkowych : 
cząstkowych, liniowych, jednorodnych. 

Równanie
:

we współrzędnych:

0

0

0

3

33

2

32

1

31

3

23

2

22

1

21

3

13

2

12

1

11























































x

x

x

x

x

x

x

x

x



















Do wyznaczenia jest 6 nieznanych 
funkcji naprężęń, przy spełnieniu trzech 
warunków brzegowych w każdym 
punkcie powierzchni ciała:

j

ij

i

q











Konieczne jest więc znalezienie dalszych równań, pozwalających 
na wyznaczenie wszystkich składowych macierzy naprężeń jako 
fonkcji zmiennych przestrzennych 

x

1

, x

2

, x

3

 .

(dla 

P

i

=0)

 

 

7

Rozkład przestrzenny 
naprężeń

Dwie 
uwagi:

1. Równanie                                    jest spełnieniem tylko jednego 

z dwu

      warunków równowagi ciała: suma wszystkich sił działających 

na ciało musi być równa zeru.

0























j

ij

i

x

P



Spełnienie drugiego warunku – suma momentów równa zero – 
prowadzi do potwierdzenia przyjętego już wcześniej założenia o 
symetrii macierzy naprężeń                  

σ

ij

= σ

ji

2.  Równanie równowagi wewnętrznej jest szczególnym przypadkiem 

równania ruchu, w którym przyspieszenie jest równe zeru (ruch 
jednostajny lub ciało znajdujace się w spoczynku). Gdy 
przyspieszenie jest różne od zera, to  po prawej stronie równania 
równowagi trzeba uwzględnić siły bezwładności d’Alamberta. Jest 
to zadanie dynamiczne teorii sprężystości.