Moduł Yanga - jest modułem sprężystości podłużnej materiału. Charakteryzuje on zdolność materiału do odkształceń podłużnych w kierunku działania siły. Moduł Y jest on stałą materiałową dla obszaru liniowych odkształceń sprężystych lub wielkością nieznacznie się zmniejszającą w obszarze sprężystości. Liniowa spręzystość jest cechą charakterystyczną stopów żelaza, dla innych tworzyw można mówić tylko o średniej wartości modułu sprężystości. Przy wyznaczaniu Moduł Yanga dla prętów grubych wykorzystujemy odkształcenie złożone jakie występuje podczas zginania umocowanego umocowanego pręta na jednym końcu, lub podpartego w dwóch miejscach pręta.

Teoria zginania obejmuje dwa założenia: 1) Przekroje poprzeczne pręta poddanego czystemu zginaniu pozostają płaskie. 2) Włókna podłużne pręta nie wywierają na siebie żadnego działania, czyli nie naciskają jedno na drugie.

Część włókien podczas zginania ulega skróceniu, a pozostała część wydłużeniu, więc ze względu na całość zjawiska musi istnieć warstwa włókien, w której długości pozostaną niezmienione. Warstwę tą nazywamy obojętną (ulega ona tylko wykrzywieniu). Taka deformację nazywamy strzałką ugięcia. Zgodnie z prawem Hookea strzałka ugięcia jest wprost proporcjonalna do siły, która wywołuje zginanie S=kP gdzie k - współczynnik zależny od rozmiarów pręta (długości, modułu sprężystości) Dla porównania prawo Hookea dla prętów ściskanych lub rozciąganych ma postać
gdzie l/EF współczynnik proporcjonalności. Prawo KOOKEA - wydłużenie względne jest wprost proporcjonalne do naprężenia normalnego. (obowiązuje ono zarówno do odkształcenia dodatniego jak i ujemnego) Prawo to ma słuszność w granicach sprężystości ciała:
gdzie E - współ proporcjonalności nazywany modułem Yanga. Odkształcenie - jest to wielkość bezwymiarowa charakteryzująca względną zmianę położenia wzajemnego P-któw materialnych ciała stałego. Odkształcenie sprężyste - występuje gdy odkształcenie po odjęciu siły zewnętrznej ustępuje. Odkształcenie plastyczne - występuje gdy odkształcenie zanika po odjęciu siły.

Powyżej granicy sprężystości ciał zaczynają się odkształcenia plastyczne. Po przekroczeniu granicy plastyczności ciało ulega rozerwaniu. Odkształcenie względne - stosunek przyrostu długości początkowej l pod wpływem naprężeń normalnych:

Wyprowadzenie wzoru

dla pręta jednostronnie utwierdzonego o przekroju prostokątnym
Metoda energetyczna 0<x<l
dla pręta podpartego na oby końcach Metoda energetyczna

s

Maxwell

Momentem bezwładności układu mechanicznego względem nieruchomej osi nazywamy wielkość fizyczną Ia równą sumie iloczynów mas wszystkich n punktów materialnych układu i kwadratów ich odległości: Ia= suma(mi*pi^2)

gdzie: Ia - moment bezwładności, mi- masa i-tego punktu pi- odległość od osi Moment bezwładności ciała jest równy Ia=całka_m(p^2 dm)=całka_V (p^2 D dV) gdzie D gęstość, p - odległość elementu dv od osi a

Tw Steinera - moment bezwładności bryły I względem dowolnej osi jest równy sumie momentu bezwładności I_C tej bryły względem osi przechodzącej przez środek masy bryły równolegle do rozważanej osi oraz iloczynu masy bryły m i kwadratu odległości d między osiami: I=Ic+md^2 gdzie:

I - moment bezwładności względem dowolnej osi Ic - moment bezwładności względem dowolnej osi przechodzącej przez środek masy m - masa bryły d odległość od nowej osi. Energia mechaniczna - energia układów punktów materialnych jest równa sumie ich energii kinetycznej i energii potencjalnej wzajemnego oddziaływania tych punktów ze sobą oraz z ciałami zewnętrznymi E=Ek+Ep Elementarny przyrost energii mechanicznej układu w ciągu małego przedziału czasu dt jest równy dE= betaARG+(deEp/de t)dt to za plusem to zmiana energii potencjalnej układu w czasie dt, beta ARG - suma algebraiczna przez elementarnych wykonanych przez wszystkie siły nie potencjalne w czasie dt

Energia mechaniczna układu zachowawczego nie ulega zmianie podczas ruchu

Zas zachowania pędu , momentu pędu , energii mechanicznej kolejno:

Wyprowadzenie wzoru:

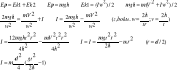
Wahadło matematyczne

Przyspieszeniem ziemskim nazywamy przyspieszenie jakie siła ciężkości nadaje ciałom swobodnie spadającym. Oznaczamy je literą g. Przy wyznaczaniu przyspieszenia największą trudność stanowi dokładny pomiar czasu. Okresem drgań T nazywamy czas, w ciągu którego zachodzi jedno pełne drganie , okres zależy jedynie od długości wahadła i od przyspieszenia ziemskiego g w danym punkcie na powierzchni ziemi. Nie zależy od masy kulki i od amplitudy wahań.

Dźwiękiem nazywamy falę mechaniczną podłużną. jest to zjawisko akustyczne. Polega na drganiu ośrodka sprężystego o częstotliwościach w zakresie słyszalnym dla ucha ludzkiego. Częstotliwość - jest to liczba identycznych zjawisk akustycznych pojawiających się okresowo na jednostkę czasu. (liczba drgań na sekundę). Wyróżniamy częstotliwość: --akustyczną - częstotliwość drgań słyszalnych zawarta w paśmie od 16 do 2000 drgań na sekundę. --drgań - liczba pełnych drgań na sekundę 1 Hz

Rodzaje fal dźwiękowych: fale akustyczne (20-20000Hz) fale interferencyjne(<20 Hz) fale ultradźwiękowe (>20kHz) Fale dźwiękowe dzielimy na: a) tony są to fale akustyczne składające się z fal harmonicznych o jednej częstotliwości b) złożone - to fale składające się z sumy fal harmonicznych. Równanie fali dźwiękowej y=Acos(kx-wt)

Interferencja jest to oddziaływanie dwóch lub więcej ruchów falowych, rozchodzących się w tym samym obszarze ośrodka, w taki sposób, że chwilowe zaburzenia fali wypadkowej są sumą wektorową chwilowych zaburzeń fal interferencyjnych.

Interferometr Quickiego. Zbudowany jest z metalowych rur. Fala głosowa od punktu A do D przechodzi przez dwa ramiona B i C. Długość ramienia C można zmienić. Dzięki temu fala w rurze D powstaje w wyniku nałożenia (interferencji) dwóch fal cząsteczkowych biegnących ramionami BiC. Jeżeli długość dróg r_B i r_C w ramionach B i C różni się o parzystą liczbę połówek fal. (r_C i r_B=2n(lambda/n) maksimum) to w ramieniu D obydwie fale wzmacniają się i obserwujemy maksymalne natężenie dźwięku. Gdy różnica jest równa nieparzystej liczbie półfal, wtedy następuje wygaszenie fali w rurze D (r_C i r_B=(2n+1)(lambda/n) minimum). Zmieniając długość ramienia C możemy uzyskać kolejne (m,n) minima oraz (M,n) maxima natężenia dźwięku w rurze D. Długość fali możemy obliczyć z różnicy dróg między dwoma max i min (r_Mn+1-r_B)-(r_min-r_B)=2(n+1)(lambda/2)-2n(lambda/2)

Źródłem dźwięku jest głośnik G zasilany z generatora akustycznego. Odbiornikiem dźwięku jest mikrofon H. Sygnał powstały w mikrofonie jest proporcjonalny do natężenia dźwięku w rurze D. Głośnik i mikrofon są izolowane akustycznie. Do zmiany ramienia C służy mechanizm śrubowy. Jego położenie S odczytujemy na podziałce. Zmiany długości są dwukrotnie większe od zmiany położenia ramienia C.
Pomiary polegają na zaobserwowaniu i zapisywaniu wskazań na podziałce S dla kolejnych S_mⁿ (n= 0,1,2,3...) dla wybranej częstotliwości z przedziału 1,5-6 kHz beta_S^M=1/n(S_n^M-S₀^M) podstawowy wzór prędkości fali podłużnej C=pier(F/g`) W przypadku fali rozchodzącej się w gazie Hooke`a pV^k=const gdzie k=Cp/Cv

Prędkość dźwięku wyraża się wzorem w gazach wraża się wzorem

zależy ona od ciśnienia , gęstości oraz stosunku stosunku Cpdo Cv ze względu na szybkość zmian ciśnienia. Prędkość można także wyrazić wzorem V=lamda*f gdzie f częstotliwość

Prędkość możemy też zapiusać że jest to pierwiastek z modułu sp®ężystości wzdłużnej do gęstości ośrodka

---