- średnia arytmetyczna ![]()
, średnia ważona : ![]()
,
dla cechy ciągłej ![]()
gdzie ![]()
- środek przedziału
Miary położenia i tendencji centralnej.
1. Wartość średnia
- średnia arytmetyczna ![]()
, średnia ważona : ![]()
,
dla cechy ciągłej ![]()
gdzie ![]()
- środek przedziału
2. Dominanta - dla cechy ciągłej :![]()
XD - dolna granica klasy, w której znajduje się dominanta
nD - liczebność przedziału dominanty
nD-1 - liczebność przedziału poprzedzającego przedział dominanty
iD - rozpiętość przedziału dominanty
3. Mediana (wartość środkowa, kwartyl drugi) Me próbki x1, x2, ... , xn ![]()
Dla cechy ciągłej
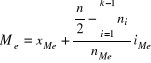
4. Kwartyl pierwszy (dla cechy ciągłej) 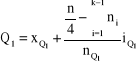
,
4. Kwartyl trzeci (dla cechy ciągłej) 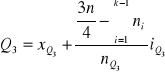
XMe, XQ 1, XQ 3 - dolne granice przedziałów, w których znajdują się mediana i kwartyle
iMe, iQ1 , iQ3 - rozpiętość przedziału mediany, kwartyla pierwszego i trzeciego
nMe, nQ1, nQ3 - liczebność przedziału mediany, kwartyla pierwszego i kwartyla trzeciego
n - ogólna liczebność populacji.
Miary rozproszenia
1. Rozstęp R = xmax - xmin
2. Wariancja ![]()
, jeśli dany szereg rozdzielczy ![]()
3. Odchylenie standardowe 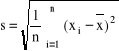
, jeśli dany szereg rozdzielczy 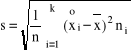
4. Współczynnik zmienności ![]()
Miary asymetrii
1. Trzeci moment centralny ![]()
, jeśli dany szereg rozdzielczy ![]()
2. Współczynnik asymetrii ![]()
3. Współczynnik skośności ![]()
Miary koncentracji
1. Moment centralny czwartego rzędu: ![]()
jeśli dany szereg rozdzielczy![]()
2. Standaryzowany moment centralny (współczynnik spłaszczenia ) ![]()
3. Kurtoza = współczynnik spłaszczenia - 3
Dystrybuanta
Dystrybuanta empiryczna
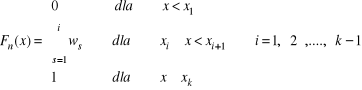
F(x) = P(X ≤ x), ![]()
,
![]()
Zmienna losowa
Dystrybuanta zmiennej losowej ciągłej ![]()
- wartość oczekiwana
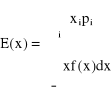
- Wariancja zmiennej losowej X
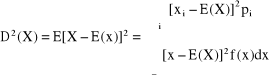
Rozkład dwumianowy ![]()
Rozkład Poissona ![]()
Rozkład prostokątny 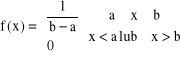
Rozkład normalny ![]()
Rozkład średniej arytmetycznej z próby dla populacji normalnej N(m, ![]()
)
Rozkład t-Studenta. ![]()
,
Rozkład różnicy średnich z prób z populacji o znanym odch. stand. σ (![]()
- ![]()
) ![]()
.
Rozkład różnicy średnich (![]()
- ![]()
) z prób pochodzących z dwóch populacji normalnych o nieznanym odchyleniu standardowym ![]()
, 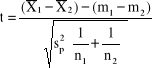
, df = n1 + n2 -2
Zmienna losowa standaryzowana. Niech X będzie zmienną losową o wartości oczekiwanej E(X) i odchyleniu standardowym D(X). Zmienną losową standaryzowaną U jest:![]()
Przedział ufności dla średniej m w populacji normalnej ze znanym odchyleniem standardowym.
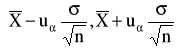
Przedział ufności dla średniej m w populacji normalnej z nieznanym odchyleniem standardowym.
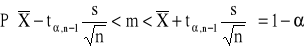
Przedział ufności dla wariancji σ2 w populacji normalnej (dla małych prób)
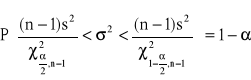
Przedział ufności dla odchylenia standardowego w populacji normalnej (dla dużych prób).
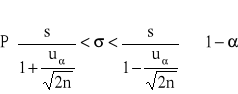
Przedział ufności dla wskaźnika struktury w populacji normalnej.
![]()
Minimalna liczebność próby.
Dla populacji o rozkładzie normalnym ze znanym odchyleniem standardowym.![]()
Dla populacji o rozkładzie normalnym ze nieznanym odchyleniem standardowym![]()
Testy statystyczne.
Test istotności dla średniej z populacji o znanym odchyleniu standardowym.
Sprawdzeniem hipotezy jest statystyka ![]()
,.
Test istotności dla średniej z populacji o nieznanym odchyleniu standardowym.
Sprawdzeniem hipotezy jest statystyka ![]()
.o rozkładzie t_Studenta dla n-1 stopni swobody
Test istotności dla dwóch średniej z populacji o znanym odchyleniu standardowym.
Sprawdzeniem hipotezy jest statystyka 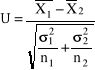
.
Test istotności dla dwóch średniej z populacji o nieznanym odchyleniu standardowym - test t Studenta
Sprawdzeniem hipotezy jest statystyka t dla n1+n2-2 stopni swobody
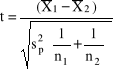
, gdzie ![]()
Test istotności dla wariancji. Sprawdzeniem hipotezy jest statystyka
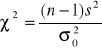
o rozkładzie chi-kwadrat o n -1 stopniach swobody
Test istotności dla dwóch wariancji. Sprawdzeniem hipotezy jest statystyka
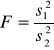
o rozkładzie F Snedecora o n1-1 i n2-1 stopniach swobody.
Test dla wskaźnika struktury. Sprawdzeniem hipotezy jest statystyka
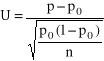
Test dla dwóch wskaźników struktury. Sprawdzeniem hipotezy jest statystyka
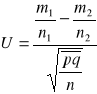
, gdzie ![]()
,![]()
![]()
Test chi-kwadrat (zgodności)
Do weryfikacji hipotezy zerowej wykorzystuje się statystykę
![]()
o rozkładzie chi -kwadrat z r-k-1 stopniami swobody
Dla zmiennej losowej skokowej
Dla zmiennej losowej ciągłej
Dla zmiennej losowej ciągłej
Dla zmiennej losowej skokowej
![]()