2. Wypływ cieczy przez małe otwory

2.1. Temat ćwiczenia

Tematem ćwiczenia jest wyznaczanie wartości współczynnika wypływu  przystawek umieszczonych w otworach, a także współczynników wydatków krótkich przewodów łączących dwa zbiorniki. W omawianym ćwiczeniu krótkie przewody łączące zbiorniki traktujemy jako otwory umieszczone w ścianie dzielącej zbiorniki. W tym przypadku rzeczywiste straty hydrauliczne występujące w tych przewodach zostają wyrażone w postaci wydatku umownego otworu o tej samej średnicy.

Omawiane ćwiczenie może zostać wykonane w następujących wariantach:

1. wyznaczanie współczynnika wydatku przystawki umieszczonej w jednym z otworów zewnętrznej ściany zbiornika w warunkach ustalonego wypływu wody ze zbiornika;

2. wyznaczanie współczynnika wydatku przystawki w warunkach nieustalonego wypływu wody ze zbiornika;

3. wyznaczanie współczynnika wydatku jednego z przewodów łączącego zbiorniki (przy traktowaniu go jako otworu) w warunkach ustalonego przepływu wody między zbiornikami;

4. wyznaczanie współczynnika wydatku przewodu łączącego zbiorniki w warunkach przepływu nieustalonego między zbiornikami.

Warianty a, b oraz c,d umożliwiają obliczenie tej samej wartości dwoma różnymi sposobami.

2.2. Wprowadzenie teoretyczne

Otworem małym nazywamy taki otwór, w którym można przyjąć istnienie jednakowej prędkości wypływu w całym przekroju poprzecznym otworu (równej prędkości w osi otworu). W praktyce można traktować niezatopiony otwór jako mały, gdy spełniony jest warunek

H/h > 5

gdzie: H - wzniesienie swobodnego zwierciadła wody w zbiorniku nad osią otworu,

h - wysokość otworu mierzona w pionie.

Przepływem ustalonym nazywamy przepływ, w którym parametry ruchu (między innymi prędkość) nie zmieniają się w czasie. Gdy warunek ten nie jest spełniony, mamy do czynienia z przepływem nieustalonym. Przy obliczaniu wypływu ustalonego z małego otworu, należy posłużyć się wzorem:

(2.1)

gdzie:

Q - natężenie wypływu przez otwór,

μ - współczynnik wydatku otworu,

A₀ - pole powierzchni otworu,

g - przyspieszenie ziemskie,

H - dla otworu niezatopionego: wzniesienie swobodnego zwierciadła cieczy w zbiorniku nad osią otworu, dla otworu zatopionego: różnica poziomów cieczy po obu stronach otworu (w obu zbiornikach).

Powyższy wzór dotyczy przypadku, gdy prędkość wody dopływającej do zbiornika może być pominięta oraz gdy ciśnienia zewnętrzne po obu stronach otworu są jednakowe.

Na podstawie podanego wyżej wzoru można obliczyć dowolny parametr, jeżeli pozostałe wielkości są znane, lub zostały pomierzone w trakcie doświadczenia. Pamiętać jednak należy, że wzór ten może być stosowany jedynie przy dowolnej, lecz stałej w czasie trwania ćwiczenia wartości H.

Stosując wzór (2.1) dla wariantu „c” ćwiczenia należy pamiętać, iż otrzymana wartość współczynnika μ będzie znacznie mniejsza niż w przypadku wariantu a. Dzieje się tak, dlatego, iż we współczynniku μ mieszczą się wszystkie straty, występujące na przewodzie łączącym.

Przy obliczaniu wypływu nieustalonego przez mały otwór (wariant „b” ćwiczenia) można wyznaczyć czas częściowego opróżnienia zbiornika za pomocą wzoru

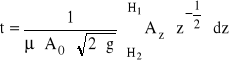
(2.2)

gdzie: t - czas częściowego lub całkowitego opróżnienia zbiornika przez otwór,

μ - współczynnik wydatku otworu,

A₀ - pole powierzchni otworu,

g - przyspieszenie ziemskie,

A_z - pole zwierciadła cieczy w zbiorniku na wysokości z nad osią otworu (w omawianym ćwiczeniu A_z=const),

z - chwilowe wzniesienie zwierciadła wody w zbiorniku nad osią otworu,

H₁ i H₂ - początkowe (H₁) i końcowe (H₂) wzniesienie poziomu wody w zbiorniku nad osią otworu.

Wzór (4.2) dotyczy również szczególnego przypadku (występującego w omawianym ćwiczeniu), gdy nie uwzględnia się prędkości opadania wody w zbiorniku v₀ ani ewentualnej różnicy ciśnień nad zwierciadłem wody w zbiorniku i w płaszczyźnie otworu. Dla A_z=const, wzór (2.2) po scałkowaniu przybiera postać

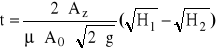
(2.3)

Przy wykonywaniu wariantu „d” ćwiczenia mamy do czynienia z wyrównywaniem się poziomów wody w obu zbiornikach (całkowitym lub częściowym). W tym przypadku wzór na czas tego wyrównania zostaje wyprowadzony na podstawie równań: ciągłości ruchu i przepływu przez otwór zatopiony. Jego ostateczna postać jest następująca (przy założeniu A₁=const i A₂=const):

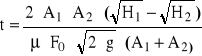
(2.4)

gdzie:

A₁, A₂ - pola powierzchni zwierciadeł wody w obu zbiornikach,

A₀ - pole przekroju przewodu łączącego zbiorniki,

μ - współczynnik wydatku umownego otworu, zastępującego przewód łączący,

H₁, H₂ - początkowa i końcowa różnica poziomów wody pomiędzy zbiornikami; w przypadku całkowitego wyrównania poziomów wody w obu zbiornikach H₂=0.

2.3. Opis modelu

Model do badania wypływu przez małe otwory przedstawiony został na schemacie stanowiska. Składa się on z dwóch zbiorników pomiarowych, zaopatrzonych w komory przelewowe. Jeden zbiornik zasilany jest wodą z instalacji wodociągowej. Aby nie nastąpiło przelewanie się wody z tego zbiornika, jej ewentualny nadmiar odprowadzany jest przez komorę przelewową. Podobnie zabezpieczony jest drugi zbiornik nr 2. Na rysunku 2.1 pokazano przykładowe konstrukcje zbiorników do pomiaru wypływu przez małe otwory.

Rys. 2.1. Zbiorniki do pomiaru wypływu przez małe otwory

W zewnętrznej ścianie drugiego zbiornika mieszczone są na jednakowym poziomie okrągłe otwory. W otworach tych montować możemy dowolne przystawki. Z otworów woda wypływa do przymocowanego pojemnika ze ścianką osłonową (zabezpieczenie przed niekontrolowanym ubytkiem wody), z którego woda wypływająca z otworu spływa do podstawionego naczynia pomiarowego.

Stanowisko wyposażone zostało w:

• pionową podziałkę (dokładność 1mm) służącą do odczytywania poziomu wody,

• kurki spustowe (po jednym przy każdym ze zbiorników),

• ścianki pionowe zamocowane do dna zbiorników, które rozpraszają energie kinetyczną strumienia wody dopływajacej, umożliwiając ich równomierne napełnianie,

• komplet przystawek,

• korki do zamykania otworów zewnętrznych zbiornika,

• naczynie pomiarowe wraz ze stoperem.

2.4. Sposób wykonania ćwiczenia

Wariant A. W celu obliczenia współczynnika wydatku μ przystawki umieszczonej w otworze zewnętrznym, samego otworu lub kurka spustowego w warunkach ustalonego wypływu wody przekształcamy odpowiednio wzór (4.1)

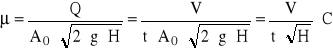
(2.5)

gdzie:

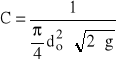
- parametr stały dla danego doświadczenia,

V - objętość cieczy zmierzona w naczyniu pomiarowym,

t - średni czas wypływu objętości V,

d_o - średnica otworu,

pozostałe oznaczenia jak we wzorze (2.1).

W celu obliczenia wartości μ należy zamontować odpowiednią przystawkę w otworze zewnętrznym, a następnie - przy otwartych przewodach łączących zbiorniki - doprowadzić wodę do modelu. Po pewnym czasie ustali się poziom wody w zbiorniku I (na poziomie przelewu), a nieco później w zbiorniku II. Po ustaleniu się obu poziomów następuje zrównanie się przepływów między zbiornikami z wypływem przez badany otwór, co oznacza spełnienie warunku przepływu ustalonego i umożliwia rozpoczęcie właściwych pomiarów. Strumień wypływającej wody określamy metodą „podstawionego naczynia” mierząc czas t zebrania w naczyniu określonej (losowej) ilości wody V. Czynność tą powtarzamy trzykrotnie. Należy także zmierzyć wzniesienie H zwierciadła wody w zbiorniku II. W efekcie możemy obliczyć wartość średnią natężenia przepływu Q.

W ten sposób wyznacza się pierwszą wartość współczynnika μ. W celu wykonania następnych serii pomiarowych należy spowodować inny, lecz stały w czasie, poziom wody w zbiorniku II. Uzyskuje się to poprzez częściowe przymknięcie jednego z zaworów na przewodach łączących zbiorniki główne. W ten sposób dla szeregu par wartości Q i H obliczamy odpowiednie wartości szukanych współczynników wydatku: μ₁, μ₂...μ_n.

Wielkości mierzone i obliczone zestawić można w formie tabelarycznej oraz przedstawic na wykresie.

Wariant B. W celu obliczenia współczynnika μ (jak w wariancie a), lecz w warunkach ruchu nieustalonego (tzn. przy opróżnianiu zbiornika II), należy przekształcić odpowiednio wzór (2.3)

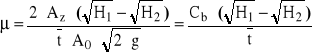
(2.6)

gdzie:

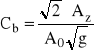
- parametr stały dla danego doświadczenia,

H₁ i H₂ - jak we wzorze (2.2),

t - średni czas częściowego opróżnienia zbiornika.

Przygotowanie modelu do pomiarów przebiega analogicznie jak w wariancie I, aż do momentu napełnienia się zbiornika II. Wówczas zamykamy zawory na wszystkich przewodach łączących zbiorniki i zamykamy również badaną przystawkę (lub otwór). Po uspokojeniu się zwierciadła wody w zbiorniku II wyjmujemy korek z otworu lub przystawki, uruchamiając tym samym wypływ cieczy z modelu. Następnie mierzymy dwoma stoperami czas, w ciągu, którego opadający poziom wody w zbiorniku II przekroczy dwie określone wcześniej, lecz dowolne, wysokości H₁ i H₂. Przy następnych seriach pomiarowych ustalamy inne przedziały wartości H₁ i H₂ i dla nich dokonujemy pomiaru czasów, obliczając średnią wielkość t.

Wyniki pomiarów i obliczeń można zestawić w formie tabelarycznej.

Wariant C. W celu wyznaczenia wartości μ jednego z przewodów łączących zbiorniki główne w warunkach przepływu ustalonego należy skorzystać ponownie z przekształconego wzoru (2.1)

(2.7)

gdzie:

H=H₁-H₂ - różnica poziomów wody w obu zbiornikach głównych (wielkość stała dla danej serii pomiarowej),

pozostałe wielkości jak we wzorach (2.1) i (2.5).

Przygotowanie modelu polega na ustaleniu takiego przepływu wody przez cały model (przy całkowicie otwartym badanym przewodzie łączącym i zamkniętych pozostałych), aby poziomy wody w obu zbiornikach głównych H₁ i H₂ były stałe. Po obliczeniu średniego czasu t oraz różnicy poziomów H można ze wzoru (2.7) wyznaczyć szukaną wartość μ.

W celu wykonania następnych serii pomiarowych należy zmienić wartość H poprzez zmianę wielkości wypływu wody z modelu lub wielkości zasilania. Nie można jednak w żadnym wypadku dokonywać jakichkolwiek regulacji zaworami umieszczonymi na przewodach łączących zbiorniki główne. Zmiany wypływu dokonać można poprzez zmianę przystawki w otworze lub za pomocą zaworu wodociągowego. Zmiana wypływu lub dopływu wody do modelu wywoła oczywiście zmianę różnicy poziomów H i umożliwi dokonanie nowej serii pomiarów.

Wielkości mierzone i obliczone można przedstawić w formie tabelarycznej.

Wariant D. W celu wyznaczenia współczynnika μ jak w wariancie poprzednim, lecz w warunkach ruchu nieustalonego korzystamy z przekształconego wzoru (2.4)

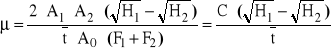
(2.8)

gdzie:

- parametr stały dla danego ćwiczenia,

t - średni czas częściowego lub całkowitego wyrównania poziomów wody w obu zbiornikach,

pozostałe oznaczenia jak we wzorze (2.4).

Przygotowanie modelu do tego wariantu ćwiczenia polega na całkowitym zamknięciu otworów odpływowych i przewodów łączących zbiorniki główne oraz napełnieniu zbiornika I przy możliwie opróżnionym zbiorniku II. Po odczytaniu poziomów wody w obu zbiornikach i  i otwieramy całkowicie zawór na badanym przewodzie łączącym, włączając zarazem dwa stopery; zatrzymujemy je jednocześnie z zamknięciem zaworu na przewodzie łączącym. Nowe poziomy wody w zbiornikach wynoszą odpowiednio i .

Zgodnie ze wzorem (2.8) obliczamy relacje H₁= - oraz H₂= - ; pozostałe wielkości mierzymy bezpośrednio na modelu i ostatecznie ze wzoru (2.8) wyznaczamy szukaną wartość μ.

Następne serie pomiarowe wykonujemy przy innych, lecz dowolnie wybranych zakresach zmian poziomów wody w obu zbiornikach.

Wielkości mierzone i obliczone zestawić można w formie tabelarycznej oraz przedstawić na wykresie.

Warto zauważyć, że w przypadku jednakowych wymiarów obu zbiorników głównych (F₁=F₂), przy prawidłowym wykonaniu pomiarów, powinny zostać spełnione równości

-=-

4.5. Uwagi końcowe

Teoretycznie wartości współczynników wydatku μ dla danego otworu lub przystawki zależą od wysokości ciśnienia, jakie panuje na wlocie do nich. W przypadku naszego doświadczenia zmiany ciśnień są jednak niewielkie i wartości powinny być dla danego otworu stałe. Praktycznie wartości: μ₁, μ₂...μ_n , otrzymane z poszczególnych serii, mogą się nieco różnić ze względu na popełniane błędy pomiarowe. W celu zminimalizowania popełnianych błędów należy przy wykonywaniu tego ćwiczenia przestrzegać poniższych zasad:

• każdy pomiar winien być wykonany trzykrotnie lub (w przypadku pomiaru czasu) dwoma stoperami,

• otwory z przystawkami muszą pracować zawsze jako swobodne (nie zatopione),

• przy wykonywaniu wariantu D doświadczenia można (mając do dyspozycji szereg stoperów) uzyskać kilka serii pomiarowych w jednym cyklu częściowego wyrównania poziomów wody,

• w wariantach A i C należy zapewnić pełną stabilizację poziomu wody w zbiorniku II,

• wszystkie pomiary dotyczące ruchu nieustalonego powinny być wykonywane w trakcie procesu napełniania lub opróżniania zbiorników, a nie obejmować całego procesu zmian poziomów wody,

• przy obliczaniu powierzchni otworu zaopatrzonego w przystawkę A₀ należy brać do obliczeń zawsze jej średnicę wylotową,

• należy pamiętać, aby wszystkie wielkości występowały w tych samych (najlepiej podstawowych) jednostkach układu SI.

2. Wypływ cieczy przez małe otwory

- 8 -

---