ALGEBRA LINIOWA
Literatura:
S.Kowalski „Algebra liniowa” - skrypt
Ciąg ( skończony )
Ciągi ( podwójne ) =: macierze
awk
w Є { 1,2, ..... m } - wiersze
k Є { 1,2, ..... n } - kolumny
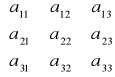
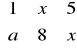
![]()
macierz kwadratowa ( w = k )
DZIAŁANIA NA MACIERZACH
Dodawanie ( warunek równości wymiarów )
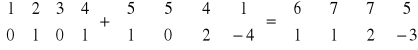
Macierz zerowa - wszystkie elementy równe 0 ( element metody dodawania )
Transponowanie macierzy ( AT ) - zamiana wiersz na kolumny
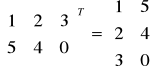
( A + B )T = AT + BT
MNOŻENIE PRZEZ LICZBY
Liczba mnożona jest przez wszystkie elementy macierzy
![]()
( α * A )T = αT * AT
MNOŻENIE MACIERZY
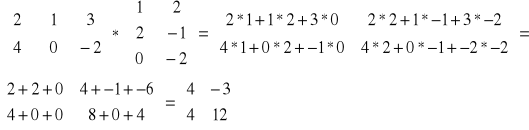
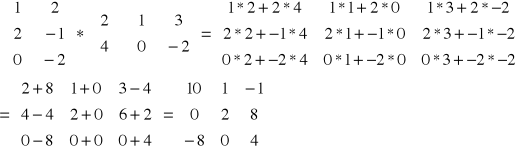
Definicja mnożenia macierzy
![]()
![]()
Mnożenie macierzy nie jest przemienne
![]()

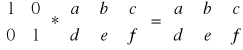
![]()
Stopień macierzy - ilość jedynek po przekątnej
![]()
![]()
![]()
MACIERZE KWADRATOWE
Wyznacznik macierzy
![]()
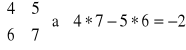
Schemat Sarrusa ( tylko do wyznaczników stopnia trzeciego )
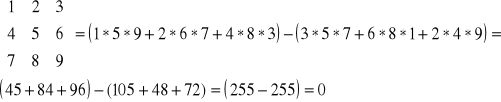
Algorytm CHIO
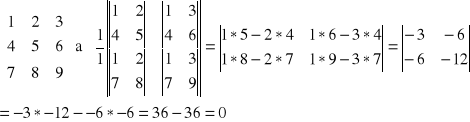
Rozwinięcie Laplase'a
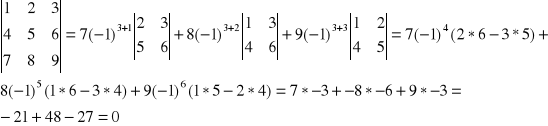
Algorytm CHIO

Wyznaczniki w arkuszach kalkulacyjnych
Excel
Berive
ZASTOSOWANIA
Odwracanie macierzy
Macierz kwadratowa jest odwracalna wtedy i tylko wtedy gdy jej wyznacznik jest różny od 0
![]()
Wzór
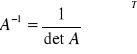
![]()
Mrs - minor ( wyznacznik ) bez r-tego wiersza s-tej kolumny
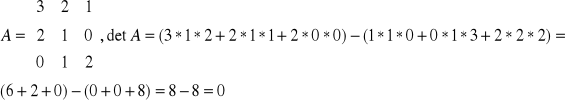
A - macierz nie jest odwracalna ( det A = 0 )
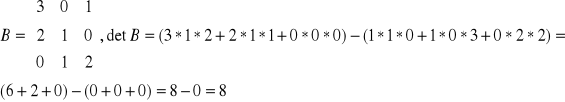
B - macierz jest odwracalna (![]()
)

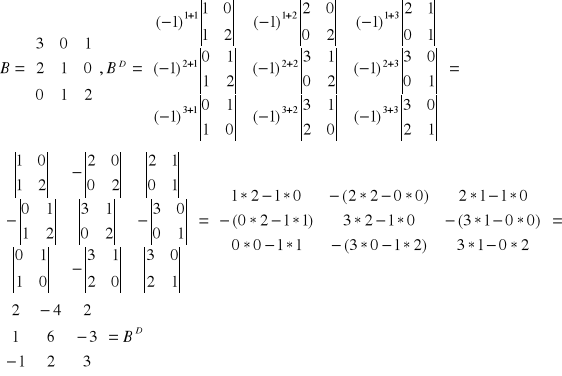
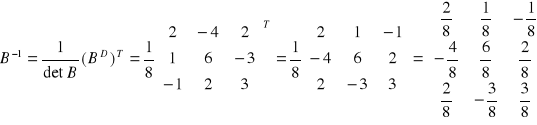
Sprawdzenie wyniku
![]()

RÓWNANIA LINIOWE
2x-y=2 - wykresem jest prosta ( w R2 )
2x+y+3z=5 - wykresem jest płaszczyzna ( w R3 )
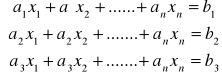
- wykresem jest płaszczyzna w ( Rn-1)
Inny zapis ( macierzowy )
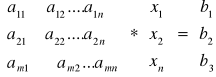
![]()
- układ równań liniowych
![]()
- macierz rozszerzona
Układy Cramera
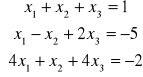
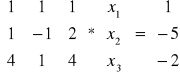
- postać macierzowa
![]()
![]()
- mam dwie metody
metoda wzorów Cramera
metoda wzorów macierzowych
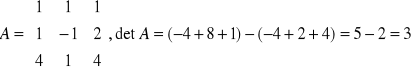
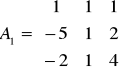
- kolumnę pierwszą zamieniamy kolumną wyrazów wolnych
![]()
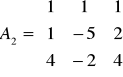
- kolumnę drugą zamieniamy kolumną wyrazów wolnych
![]()
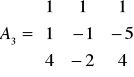
- kolumnę trzecią zamieniamy kolumną wyrazów wolnych
![]()
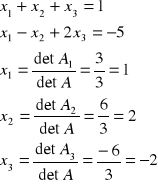
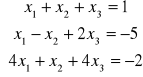
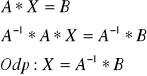
Metoda macierzy odwrotnych
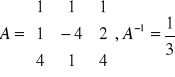
![]()
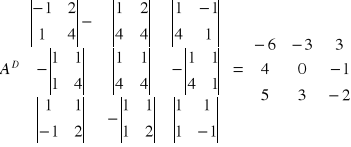
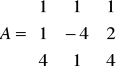
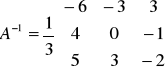
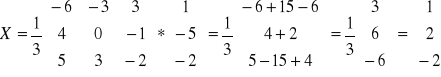
Eliminacja Gaussa
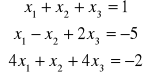
Operacje elementowe
![]()
- zamiana r-tego równania z s-tym
![]()
- r-te równanie pomnożone przez ![]()
![]()
- r-te równanie pomnożone przez ![]()
dodajemy do s-tego
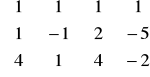
- macierz rozszerzona
Macierz występuje w postaci normalnej jeżeli:
pierwszy niezerowy element wiersza jest
jeżeli w kolumnie jest to pozostałe elementy tej kolumny są zerami
przemieszcza się schodkowo w prawo
wiersze zerowe są po niezerowych
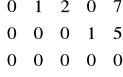
- macierz jest w postaci normalnej
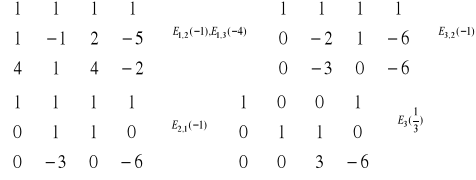
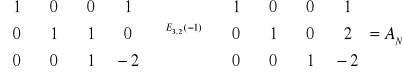
- postać normalna
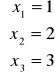
Rząd macierzy
Liczba niezerowa wierszy w postaci normalnej tych macierzy
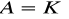
w macierzy A istnieje niezerowy minor stopnia K oraz nie istnieją niezerowe minory stopnia wyższego
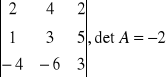
Odp: rząd macierzy równy 3
Przykład:
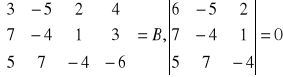
- wszystkie macierze 3-go stopnia są zerowe
Odp: rząd macierzy = 2 rzB=2
Twierdzenie ( Konecker, Capelli)
Układ równań A*X=B ma rozwiązanie wtedy i tylko wtedy gdy ![]()
2000-09-15
Przestrzenie liniowe
![]()
- zbiór macierzy K=1 ( kolumnowy )
R3 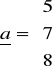
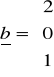
Macierz kolumnowa - wektor
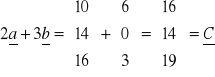
- C jest kombinacją liniową wektorów a i b
![]()
wtedy i tylko wtedy gdy istnieją liczby ![]()
i![]()
takie, że ![]()
![]()
- współczynniki kombinacji
Przedstaw wektor ![]()
w postaci kombinacji liniowej wektorów
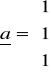
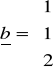
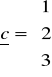
![]()
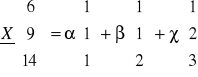
Przestrzenie z iloczynem skalarnym
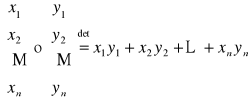
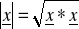
- długość ( norma )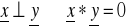
- ortogonalność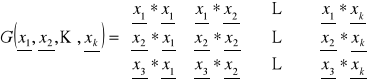
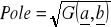
![]()
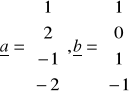
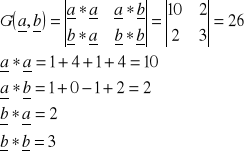
Pole równe jest pierwiastkowi z wyznacznika ![]()
Ortogonalizacja bazy metodą Gramma - Smidtha
![]()
- baza
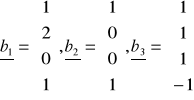
Czy to jest baza ?
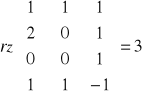
( największy niezerowy minor macierzy )
Jeżeli rząd macierzy jest równy liczbie generatorów to jest to baza, jeżeli rząd macierzy jest mniejszy od liczby generatorów to nie jest to baza.
Nowa baza ( ortogonalna )
![]()
I wektor
O1 wybieramy dowolnie spośród wektorów bazy B. Np.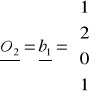
II wektor O2 określa się następująco
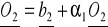
z warunkiem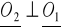
( ortogonalny )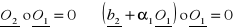
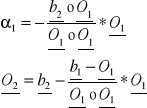
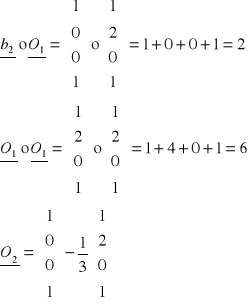
I3- macierz jednostkowa 3-go stopnia
Macierz jednostkowa stopnia 2-go
determinanta
Macierz dołączona
Ad, AD, adj A
macierz
główna
macierz
niewiadoma
kolumna wyrazów wolnych
wyrazy wolne
macierz kwadratowa
Wzory Cramera
skalary
b
a
a
b
w kolumnach są generatory
c
Wyszukiwarka
Podobne podstrony:
(5169) algebra liniowa - wyk
Algebra liniowa i geometria kolokwia AGH 2012 13
Algebra 1 03 wymiar i baza przestrzeni liniowej
Algebra Liniowa 2 Definicje Twierdzenia Wzory Jurlewicz Skoczylas
Egzamin z Algebry Liniowej 2004
Geometia i Algebra Liniowa
Poprawa 1 go kolokwium z algebry liniowej
do wydruku sc, WTD, algebra liniowa
Algebra liniowa 1B Definicje
LICZBY ZESPOLONE I ALGEBRA LINIOWA M GRZESIAK
Algebra liniowa1 id 57289 Nieznany
[Algebra liniowa 1 definicje, twierdzenia, wzory] [Jurlewicz, Skoczylas]
Analiza i Algebra liniowa semestr 2 Politechnika koszalińska kierunek informmatyka
Algebra 1 05 jądro i obraz przekształcenia liniowego
Algebra liniowa macierze
alg-e, WTD, algebra liniowa
Algebra liniowa ściąga
więcej podobnych podstron