WOJSKOWA AKADEMIA TECHNICZNA
LABOLATORIUM FIZYCZNE
Grupa szkoleniowa IG-14d Podgr. 3 ...................................................
(stopień i nazwisko
prowadzącego ćwiczenia)
Stańdo Łukasz
.............................. ..............................
(ocena przygot. (ocena końcowa)
do ćwiczenia)
SPRAWOZDANIE
z
PRACY LABOLATORYJNEJ Nr 1
WYZNACZANIE DŁUGOŚCI FALI ŚWIETLNEJ ZA POMOCĄ SIATKI DYFRAKCYJNEJ
1.Wstęp teoretyczny
Celem ćwiczenia jest wyznaczenie długości fali świetlnej za pomocą siatki dyfrakcyjnej. Zjawisko rozchodzenia się fal można opisać za pomocą zasady Huyghensa, według której każdy punkt ośrodka, do którego dociera czoło fali, staje się samodzielnym źródłem wysyłającym elementarne fale kuliste.
Dyfrakcją (ugięciem fali) nazywamy zjawisko zniekształcenia powierzchni falowej, które jest spowodowane przeszkodą stojącą na drodze jej rozchodzenia się.
Fale świetlne, polegają na rozchodzeniu się zmiennych pól: elektrycznego sprzężonego z nim nierozdzielnie pola magnetycznego. W zjawisku interferencji światła polegającym na nakładaniu się fal świetlnych wektory fal świetlnych dodają się. Fale o jednakowych długościach wzmacniają się najsilniej jeżeli różnica ich dróg optycznych jest równa wielokrotności długości fali ( max gdy Δl=dsinα=kλ , przy k=0,±1,±2,...), a maksymalnie się osłabiają, jeżeli różnica ich dróg optycznych jest równa wielokrotności połówek długości fali [min gdy dsinα = (k+0,5)λ , przy k=0,±1,±2,...). Zjawisko interferencji przedstawił Young w swym doświadczeniu, które polegało na ustawieniu trzech równoległych do siebie a zarazem prostopadłych do promieni światła słonecznego ekranów (rys. poniżej).
Zgodnie z zasadą Huyghensa otworek Z0 działa jako źródło rozchodzących się elementarnych fal kulistych, które padając na otworki Z1 i Z2 umieszczone w ekranie E2 ponownie generują dwie fale kuliste. Na ekranie E3 Young otrzymał szereg rozłożonych na przemian jasnych i ciemnych prążków. Aby w przedstawionym zjawisku mogła wystąpić interferencja światła, przedtem musiało zaistnieć zjawisko dyfrakcji. Takie następstwo jest charakterystyczne dla wielu doświadczeń interferencyjnych, także dla wykonywanego w ćwiczeniu doświadczenia z siatką dyfrakcyjną.
Liczbę k nazywamy rzędem obrazu interferencyjnego, im większy rząd tym słabszy obraz interferencyjny na ekranie gdyż wzrasta kąt ugięcia światła.
Siatka dyfrakcyjna nazywamy zbiór dużej liczby jednakowych, równoległych szczelin,
miedzy którymi występują równe odstępy co określamy jako stała siatki dyfrakcyjnej i oznaczamy literą d. Siatki dyfrakcyjne dzielą się na transmisyjne i odbiciowe. Rzucając na siatkę dyfrakcyjna monochromatyczna wiązkę promieni równoległych, możemy obserwować w płaszczyźnie ogniskowej soczewki zbierającej obraz dyfrakcyjny, będący zbiorem prążków interferencyjnych. Miedzy promieniami padającymi a ugiętymi powstaje kat określony stosunkiem -λ/d, a względne natężenie prążków zależy od stosunku λ/a. Kat pod jakim ugięte jest k-te widmo interferencyjne zależy od długości fali oraz od stałej siatki d: ![]()
Opis układu pomiarowego
Źródłem światła Z dającym widmo liniowe (lampa rtęciowa lub sodowa) oświetlamy wąską (~1mm) prostokątną szczelinę na ekranie E. Wiązka promieni po przejściu przez szczelinę w ekranie pada na siatkę dyfrakcyjną. Promienie przez nią ugięte wchodzą do umieszczonego za siatką oka ludzkiego. Na przedłużeniu wiązek ugiętych wchodzących do oka, obserwator ujrzy na tle ekranu pozorne widmo źródła światła utworzone przez siatkę dyfrakcyjną (szereg prążków barwnych z prawej i lewej strony szczeliny).
2. Przykładowe obliczenia
-wartość średnia położeń prążków
![]()
-sinus kątów ugięcia linii widma
-barwa czerwona
-rząd I
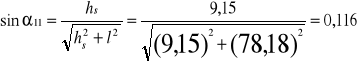
-rząd II
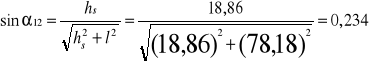
-barwa zielona
-rząd I
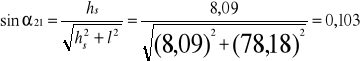
-rząd II
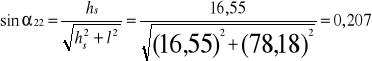
-długość fal mierzonych przy d=5,2 ± 1μm
![]()
-średnia długość fal danej barwy
![]()
RACHUNEK BŁĘDÓW
-odchylenie standardowe
![]()
![]()
![]()
|
||||||
l.p. |
I rząd |
II rząd |
||||
|
h[cm] |
h-hs[cm] |
(h-hs)²[cm] |
h[cm] |
h-hs[cm] |
(h-hs)²[cm] |
1 |
9,20 |
0,05 |
0,0025 |
19,00 |
0,14 |
0,0196 |
2 |
9,30 |
0,15 |
0,0225 |
18,80 |
-0,06 |
0,0036 |
3 |
9,15 |
0,00 |
0,0000 |
18,80 |
-0,06 |
0,0036 |
4 |
9,15 |
0,00 |
0,0000 |
18,70 |
-0,16 |
0,0256 |
5 |
9,15 |
0,00 |
0,0000 |
18,90 |
0,04 |
0,0016 |
6 |
9,10 |
-0,05 |
0,0025 |
18,95 |
0,09 |
0,0081 |
7 |
9,05 |
-0,10 |
0,0100 |
18,70 |
-0,16 |
0,0256 |
8 |
9,20 |
0,05 |
0,0025 |
19,00 |
0,14 |
0,0196 |
9 |
9,10 |
-0,05 |
0,0025 |
18,90 |
0,04 |
0,0016 |
10 |
9,15 |
0,00 |
0,0000 |
18,90 |
0,04 |
0,0016 |
Suma |
0,0425 |
suma |
0,1105 |
|||
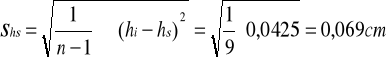
BARWA ZIELONA |
||||||
l.p. |
I rząd |
II rząd |
||||
|
h[cm] |
h-hs[cm] |
(h-hs)²[cm] |
h[cm] |
h-hs[cm] |
(h-hs)²[cm] |
1 |
8,15 |
0,06 |
0,0036 |
16,60 |
0,05 |
0,0025 |
2 |
8,25 |
0,16 |
0,0256 |
16,55 |
0,00 |
0,0000 |
3 |
8,10 |
0,01 |
0,0001 |
16,60 |
0,05 |
0,0025 |
4 |
8,05 |
-0,04 |
0,0016 |
16,50 |
-0,05 |
0,0025 |
5 |
8,10 |
0,01 |
0,0001 |
16,50 |
-0,05 |
0,0025 |
6 |
8,10 |
0,01 |
0,0001 |
16,50 |
-0,05 |
0,0025 |
7 |
7,85 |
-0,24 |
0,0576 |
16,35 |
-0,20 |
0,0400 |
8 |
8,10 |
0,01 |
0,0001 |
16,70 |
0,15 |
0,0225 |
9 |
8,10 |
0,01 |
0,0001 |
16,60 |
0,05 |
0,0025 |
10 |
8,10 |
0,01 |
0,0001 |
16,60 |
0,05 |
0,0025 |
Suma |
0,0890 |
suma |
0,0800 |
|||
![]()
-względne odchylenie:
-barwa czerwona
-rząd I
![]()
-rząd II
![]()
-barwa zielona
-rząd I
![]()
-rząd II
![]()
-względny błąd (∆l=0,2cm):
-barwa czerwona
-rząd I
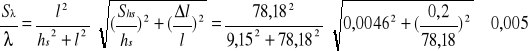
-rząd II
![]()
-barwa zielona
-rząd I
![]()
-rząd II
![]()
-bezwzględna wartość odchylenia
-barwa czerwona
-rząd I
![]()
![]()
-rząd II
![]()
-barwa zielona
-rząd I
![]()
-rząd II
![]()
-średnia bezwzględnej wartości odchylenia
-barwa czerwona
![]()
-barwa zielona
![]()
3.Tabela wyników pomiarów
|
k |
lp. |
hp [cm] |
hl [cm] |
hs [cm] |
shs [cm] |
l [cm] |
Δl [cm] |
λ [μm] |
λs [μm] |
sλ [μm] |
sλs [μm] |
Barwa 1 (czerwony)
|
1
|
1. 2. 3. 4. 5. |
9,20 9,30 9,15 9,15 9,15 |
9,10 9,05 9,20 9,10 9,15 |
9,15
|
0,069
|
78,18
|
0,002
|
0,603
|
0,6055
|
0,0030
|
0,0033
|
|
2
|
1. 2. 3. 4. 5. |
19,00 18,80 18,80 18,70 18,90 |
18,95 18,70 19,00 18,90 18,90 |
18,86
|
0,110
|
|
|
0,608
|
|
0,0036
|
|
Barwa 2 (zielony)
|
1
|
1. 2. 3. 4. 5. |
8,15 8,25 8,10 8,05 8,10 |
8,10 7,85 8,10 8,10 8,10 |
8,09
|
0,099
|
78,18
|
0,002
|
0,535
|
0,5365
|
0,0059
|
0,0043
|
|
2 |
1. 2. 3. 4. 5. |
16,60 16,55 16,60 16,50 16,50 |
16,50 16,35 16,70 16,60 16,60 |
16,55 |
0,094 |
|
|
0,538 |
|
0,0027 |
|
-Przyczyną błędów systematycznych może być niedokładne ustawienie sznurka na określonym pasku, a co za tym idzie niedokładny odczyt wartości z linijki. Kolejną przyczyną może być ustawienie głowy w trakcie odczytu (zmienna odległość oka od siatki dyfrakcyjnej, różne kąty pod jakimi się patrzy) również błędy zależą od wzroku obserwatora.
WNIOSKI I OCENA OTRZYMANYCH REZULTATÓW
Celem ćwiczenia było wyznaczenie długości fal świetlnych za pomocą siatki dyfrakcyjnej, z moich pomiarów i obliczeń wynika że średnia długość fali dla barwy czerwonej wynosi λs=0,6055 μm a dla barwy zielonej λs=0,5365 μm . Porównując otrzymane wyniki z wartościami podanymi w tablicach wynika , że przeprowadzone doświadczenie mimo swej prostoty umożliwia dokonanie dość dokładnych pomiarów (różnica wartości otrzymanych i tablicowych wynosi w moim przypadku ±0,05 μm).
Względny błąd dla barwy czerwonej I rzędu wynosi 0.005 , II rzędu 0.006 a dla barwy zielonej I rzędu 0,011, II rzędu 0,005. Przyczyny powstawania tego błędu opisałem powyżej a głównie wynikają one z winyi osoby przeprowadzającej ćwiczenie.
Pracę wykonał: ......................................................... dnia 22 marzec 2004r.
(podpis)
Uwagi prowadzącego ćwiczenia:
8
E3
E3
E2
E1
Z2
Z1
Z0
Światło słoneczne
Intensywność
Z
Wyszukiwarka
Podobne podstrony:
28, Lab 28, WOJSKOWA AKADEMIA TECHNICZNA
Wojskowa Akademia Techniczna8
Rynek pracy, Wojskowa Akademia Techniczna - Zarządzanie i Marketing, Licencjat, II Rok, Semestr 3, R
Formy pieniądza, Wojskowa Akademia Techniczna - Zarządzanie i Marketing, Licencjat, II Rok, Semestr
BADANIA, Wojskowa Akademia Techniczna - Zarządzanie i Marketing, Licencjat, II Rok, Semestr 4, Badan
Ustanie stosunku pracy, Wojskowa Akademia Techniczna - Zarządzanie i Marketing, Licencjat, II Rok, S
Pytania z nr folii + odpowiedzi, Wojskowa Akademia Techniczna (WAT), Lokalne Sieci Komputerowe, Zali
Wojskowa Akademia Techniczna
Wojskowa Akademia Techniczna
Czas pracy, Wojskowa Akademia Techniczna - Zarządzanie i Marketing, Licencjat, II Rok, Semestr 3, Po
5. Wykład MP, Wojskowa Akademia Techniczna (WAT), Obwody i Sygnały, Materiały 2013
8. Wykład, Wojskowa Akademia Techniczna (WAT), Obwody i Sygnały, Materiały 2013
6. Wyklad MP, Wojskowa Akademia Techniczna (WAT), Obwody i Sygnały, Materiały 2013
ZARZADZANIE-STRATEGICZNE-1, Wojskowa Akademia Techniczna - Zarządzanie i Marketing, Licencjat, II Ro
mojeok, Wojskowa Akademia Techniczna
21++, Ćwiczenia nr 21, WOJSKOWA AKADEMIA TECHNICZNA
Tworzenie łańcucha wartości dodanej, Tworzenie Łańcucha Wartości Dodanej, WOJSKOWA AKADEMIA TECHNI
LAB 36, WOJSKOWA AKADEMIA TECHNICZNA
więcej podobnych podstron