LABORATORIUM FIZYCZNE

GRUPA LAB. IX

Kolejny nr ćwiczenia :

2

Nazwisko i imię :

Wydział

Symbol ćwiczenia :

17

ETI

Temat : Pomiar strat ciepłą w zależności od różnicy temperatur

Data odr. ćwiczenia: 21 X

Sem. I

Data odd. sprawozdania: 28 X

Grupa st. II

Ocena

Podpis asystenta

Pomiar strat ciepła w zależności od różnicy temperatur

1. Wstęp teoretyczny

Ciała ogrzane tracą część swojej energii cieplnej, przekazując ją do otoczenia chłodniejszego. Straty te mogą zachodzić poprzez:

1. Przewodnictwo

2. Konwekcję

3. Promieniowanie

Procesy te trwają tak długo, dopóki temperatura ciała nie zrówna się z temperaturą otoczenia. W czasie podgrzewania ciała część energii dostarczanej do niego zwiększa jego energię wewnętrzną (temperaturę), pozostałą część ciało traci w wyniku wyżej wymienionych procesów.

Promieniowanie cieplne padające na jakieś ciało pozostaje przynajmniej częściowo przez nie pochłonięte, zamienione ponownie na ciepło podwyższające temperaturę. Stan w którym temperatury stykających się ciał całkowicie się wyrównają, tzn. temperatura ciała i otoczenia będzie taka sama, nazywamy stanem równowagi termicznej.

Jeżeli:

• P - moc źródła ciepła

• K - pojemność cieplna ciała

• q - straty ciepła na jednostkę czasu

• dT - zmiana temperatury ciała w czasie dτ

to wtedy bilans cieplny dla przedziału czasu dτ przyjmuje postać:

Dla niezbyt dużych zmian temperatury, straty ciepła q są w przybliżeniu proporcjonalne do różnicy temperatur ciała T i otoczenia T₀ i można wyrazić to wzorem Newtona:

gdzie a jest stałą dla danego ciała, zależną w istotny sposób od wielkości i rodzaju powierzchni zewnętrznej ciała oraz od warunków panujących w otoczeniu.

Podstawiając t za różnicę temperatur T-T₀ otrzymujemy:

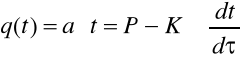
gdzie
oznacza szybkość zmiany temperatury ciała o temperaturze o
wyższej od temperatury otoczenia.

Po rozwiązaniu powyższego równania różniczkowego dla warunku początkowego, że w chwili τ=0 temperatura ciała jest równa temperaturze zewnętrznego środowiska, tj. t=0, otrzymujemy zależność t=F(τ) w postaci;

gdzie:

Ze wzoru tego wynika, że dla τ∞ temperatura t zmierza do temperatury granicznej:

odpowiadającej występowaniu równowagi cieplnej, w której ciepło dostarczone do ciała przez źródło jest całkowicie przekazywane przezeń do otoczenia. Ponieważ temperatura ciała nie ulega wtedy zmianie, oznacza to, że:

2. Schemat układu pomiarowego

Układ stanowi naczynie metalowe wypełnione wodą, w której zanurzone są: grzałka elektryczna, mieszadełko i sonda termometru. Grzałka jest podłączone do zasilacza sieciowego o regulowanym napięciu wyjściowym. W obwodzie elektrycznym układy badanego znajduje się woltomierz V i amperomierz A.

3. Pomiary i obliczenia

Tabela niżej przedstawia wyniki pomiaru temperatury cieczy, natężenia prądu i napięcia oraz policzoną z tych wartości moc cieplną grzałki w różnych odstępach czasu (pierwsze 20 minut - co 2 minuty, potem co 5 minut - do 90 minuty)

Temperatura otoczenia T₀ w chwili τ=0 wynosiła 21,3 °C

l.p.	Czas τ [min]	Temperatura T [°C]	Natężenie prądu I [A]	Napięcie U [V]	Moc źródła P [W]
1	0	21,3 ±0,1	1,00	25,7	25,7
2	2	22,0 ±0,1	1,00	25,7	25,7
3	4	22,6 ±0,1	1,00	25,7	25,7
4	6	23,2 ±0,1	1,00	25,7	25,7
5	8	23,8 ±0,1	1,00	25,7	25,7
6	10	24,3 ±0,1	1,00	25,7	25,7
7	12	24,8 ±0,1	1,00	25,7	25,7
8	14	25,4 ±0,1	1,00	25,7	25,7
9	16	25,9 ±0,1	1,00	25,7	25,7
10	18	26,4 ±0,1	1,00	25,7	25,7
11	20	26,8 ±0,1	1,00	25,7	25,7
12	25	28,0 ±0,1	1,00	25,7	25,7
13	30	29,2 ±0,1	1,00	25,7	25,7
14	35	30,3 ±0,1	1,02	25,9	26,4
15	40	31,3 ±0,1	1,02	25,9	26,4
16	45	32,2 ±0,1	1,02	25,8	26,3
17	50	33,2 ±0,1	1,02	25,9	26,4
18	55	34,1 ±0,1	1,02	25,9	26,4
19	60	35,0 ±0,1	1,02	25,9	26,4
20	65	35,8 ±0,1	1,02	25,8	26,3
21	70	36,6 ±0,1	1,02	25,8	26,3
22	75	37,4 ±0,1	1,02	25,8	26,3
23	80	38,0 ±0,1	1,02	25,8	26,3
24	85	38,7 ±0,1	1,02	25,8	26,3
25	90	39,3 ±0,1	1,02	25,7	26,2

Błąd bezwzględny pomiaru temperatury wynosi

Średnia moc grzałki P wynosi 26,0 W

Podstawę do wyznaczenia wielkości charakteryzujących układ i straty ciepła stanowi wzór:

z którego wynika relacja:

gdzie:

sporządzamy tabelę wartości doświadczalnych:

T [ ^oC ]	ti [^oC]	τ [s]	dt[^oC]	dτ [min]	()ti
22,3	1	169	1	2,81	0,356
23,3	2	375	1	3,43	0,291
24,3	3	600	1	3,75	0,267
25,3	4	862	1	4,37	0,229
26,3	5	1069	1	3,45	0,290
27,3	6	1331	1	4,37	0,229
28,3	7	1575	1	4,07	0,246
29,3	8	1837	1	4,37	0,229
30,3	9	2100	1	4,38	0,229
31,3	10	2400	1	5,00	0,200
32,3	11	2720	1	5,33	0,188
33,3	12	3020	1	5,00	0,200
34,3	13	3337	1	5,28	0,189
35,3	14	3712	1	6,25	0,160
36,3	15	4125	1	6,88	0,145
37,3	16	4481	1	5,93	0,169
38,3	17	4950	1	7,82	0,128
39,3	18	5400	1	7,50	0,133

t_i = T_i - T₀

Wartości ()_ti wyznaczone zostały z wykresu otrzymanego po wykonaniu pomiarów. Wyniki zamieszczone są w powyższej tabeli .

Zadaniem jest obliczenie wartości współczynników ,  , pojemności cieplnej układu K oraz temperatury t_k, czyli temperatury do jakiej można ogrzać wodę w zadanych warunkach.

Jak widać, zależność ta jest liniowa i metodą najmniejszych kwadratów obliczamy wartości współczynników  i .

Wykres zależności pochodnej przyrostu temperatury po czasie od czasu

(musiałem na wykresie użyć innego oznaczenia)

wiedząc że:

otrzymujemy:

podstawiając wartości  i  otrzymujemy:

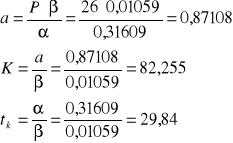
Temperatura, do której możemy podgrzać układ wynosi T₀ + t_k = 21,3 + 29,8 = 51,1°C

Wartości teoretyczne wyznaczyliśmy podstawiając obliczone P, a i K do wzoru:

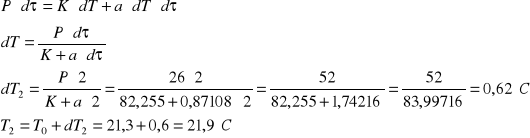
dla dτ=0,2,4,6,8,10,12,14,16,18,20,25,30,35,...,90min i obliczając dT.

Tabela wartości teoretycznych

l.p.	Czas τ [min]	Temperatura T [°C]
1	0	21,3
2	2	21,9
3	4	22,5
4	6	23,1
5	8	23,6
6	10	24,1
7	12	24,6
8	14	25,1
9	16	25,6
10	18	26,1
11	20	26,5
12	25	27,5
13	30	28,5
14	35	29,4
15	40	30,2
16	45	30,9
17	50	31,6
18	55	32,3
19	60	32,9
20	65	33,5
21	70	34,0
22	75	34,5
23	80	35,0
24	85	35,4
25	90	35,9

Skala błędu =10¹ (0,1°C ma wartość jednej jednostki = 1°C)

4. Wnioski

Analizując wyniki okazało się, że wartości teoretyczne są mniejsze od otrzymanych z pomiarów. Wpływ na to mógł mieć wzrost temperatury otoczenia podczas pomiaru (pomiar odbywał się rano, więc temperatura pomieszczenia mogła wzrosnąć podczas pomiarów ze względu na obecność wielu osób), lub błędy przyrządów pomiarowych (termometr, amperomierz lub woltomierz). Przeprowadzone doświadczenie pokazało, że przy pomocy pomiaru pewnych wartości możemy metodą regresji liniowej otrzymać wykres zależności między badanymi wielkościami oraz znaleźć wartości teoretyczne. Zmierzyliśmy pojemność cieplną naszego układu. Zauważyliśmy również, że każdy układ do którego jest dostarczana energia cieplna dąży do temperatury granicznej, to znaczy takiej, gdy cała dostarczona energia jest oddawana otoczeniu. Zjawisko to przydatne jest między innymi w elektronice, gdyż dzięki zbliżeniu temperatury granicznej np. procesora do temperatury otoczenia jesteśmy w stanie przewidzieć do jakiej maksymalnej temperatury będzie się nagrzewał w trakcie pracy w określonych warunkach. Pozwala to na lepsze określenie jego charakterystyk oraz takie budowanie układu (wentylator, radiator), aby temperatura graniczna była jak najbliższa temperaturze w której procesor najlepiej pracuje.

---