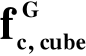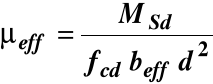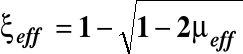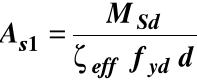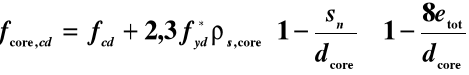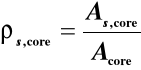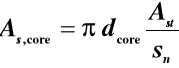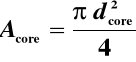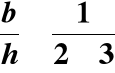LITERATURA
PN-B-03264:2002 Konstrukcje betonowe, żelbetowe i sprężone
Obliczenia statyczne i projektowanie
Podstawy projektowania konstrukcji żelbetowych
wg Eurokodu 2
Pod redakcją Mieczysława Kamińskiego,
PWN, Wrocław, 1996
Konstrukcje betonowe. Projektowanie belek, słupów i płyt żelbetowych.
M. Kamiński, J. Pędziwiatr, D. Styś,
DWE, Wrocław, 1999
Projektowanie konstrukcji żelbetowych
Andrzej Łapko, Arkady, 2000
Obliczanie przekrojów w elementach betonowych i żelbetowych
K. Grabiec, J. Bogucka, T. Grabiec-Mizera, Arkady, 2002
Projektowanie konstrukcji żelbetowych
M. Kamiński, J. Pędziwiatr, D. Styś,
DWE, Wrocław, 2004
Projektowanie elementów żelbetowych
Małgorzata Murkowska,
Wydawnictwo Politechniki Poznańskiej, 2005
Podstawy projektowania i algorytmy obliczeń konstrukcji żelbetowych
A. Łapko, B. Ch. Jensen, Arkady, 2005
---------------------------------------------------------------------------------
Konstrukcje żelbetowe
Jerzy Kobiak, Wiesław Stachurski, Arkady, 1984- 1991
Konstrukcje żelbetowe
Włodzimierz Starosolski, PWN, 2004
Konstrukcje betonowe. Przykłady obliczeń statycznych.
Kalikst Grabiec, PWN, 1996
Konstrukcje betonowe
K. Dąbrowski, W. Stachurski, J. Zieliński, Arkady 1982
WSTĘP
Pierwsze konstrukcje z betonu wzmocnionego wkładkami stalowymi zaczęto wznosić w latach siedemdziesiątych XIX w.
Minęło więc ponad sto lat, kiedy beton zbrojony prętami stalowymi, który można formować w dowolne kształty zrewolucjonizował architekturę.
Dziś konstrukcje żelbetowe stosowane są we wszystkich gałęziach budownictwa.
Podstawowe rodzaje konstrukcji betonowych różniące się mechanizmem pracy oraz zastosowaniem to;
konstrukcje betonowe
-beton nie zbrojony stalą lub ze zbrojeniem mniejszym od
minimalnego,
zastosowanie: niektóre fundamenty, posadzki, ściany oporowe.
konstrukcje żelbetowe
-beton wzmocniony celowo rozmieszczonymi prętami ze stali zbrojeniowej,
zastosowanie: we wszystkich dziedzinach budownictwa.
konstrukcje sprężone
-beton sprężany zazwyczaj cięgnami stalowymi, w
zależności od sposobu przekazania siły sprężającej
rozróżnia się:
-strunobeton,
-kablobeton,
zastosowane: dźwigary i płyty stropowe oraz dachowe o dużych
rozpiętościach, zbiorniki, konstrukcje specjalne.
Z punktu widzenia metod wykonawczych rozróżnia się:
konstrukcje monolityczne
wykonywane na miejscu wbudowania,
zaletą jest duża sztywność konstrukcji, wadą długi okres realizacji
obiektu,
konstrukcje prefabrykowane
montowane z fabrycznie wykonanych prefabrykatów,
zaletą jest szybkość realizacji, natomiast wadą mała sztywność konstrukcji,
konstrukcje monolityczno-prefabrykowane
wykonywane z monolitycznego żelbetu i elementów prefabrykowanych,
które mogą niekiedy spełniać rolę deskowań.
KONCEPCJA ŻELBETU
Polega na stworzeniu takiego połączenia betonu i stali, w którym :
siły rozciągające przejmuje stal,
siły ściskające przejmuje beton.
Celowość zespolenia betonu i stali wynika z własności mechanicznych tych materiałów.
WYTRZYMAŁOŚĆ |
BETON |
STAL |
na ściskanie |
10-60 MPa |
200-600 MPa |
na rozciąganie |
1-5 MPa |
|
BETON ma wiele cech wspólnych z kamieniem naturalnym.
Podobnie jak kamień zalicza się do materiałów kruchych.
Wytrzymałość betonu na rozciąganie jest niewielka i wynosi około 10% jego wytrzymałości na ściskanie.
Betony o wysokich wytrzymałościach są jeszcze bardziej kruche (patrz tabela).
STAL natomiast posiada wielokrotnie wyższą od betonu wytrzymałość na ściskanie jak i na rozciąganie.
Współpracę obu materiałów zilustrowano na przykładzie belki zginanej swobodnie podpartej.
Rys. Schemat pracy belki swobodnie podpartej
betonowej
żelbetowej
BELKA BETONOWA ulega zniszczeniu (złamaniu) w sposób nagły, niesygnalizowany pod wpływem niewielkiego obciążenia.
Beton w strefie rozciąganej osiąga bowiem swoją wytrzymałość na rozciąganie, która jest 10 razy mniejsza niż wytrzymałość na ściskanie.
W BELCE ŻELBETOWEJ zarysowanie elementu przebiega stopniowo.
Po pojawieniu się rys w strefie rozciąganej siły rozciągające przejmuje stal. Belka może być nadal obciążana aż do momentu , w którym beton strefy ściskanej osiągnie swoją wytrzymałość na ściskanie.
Odpowiednio dobrane pręty stalowe pozwalają belce przenosić obciążenie, aż do osiągnięcia przez beton wytrzymałości na ściskanie.
WSPÓŁPRACA BETONU I STALI
Cechy mechaniczne obu materiałów są bardzo zróżnicowane ale ich współpraca jest możliwa i celowa.
Istnienie sił przyczepności jest jednym z najważniejszych
warunków poprawnego funkcjonowania żelbetu.
W procesie twardnienia beton silnie przywiera do stali.
Po przyłożeniu obciążenia sąsiednie włókna betonu i stali
mają jednakowe odkształcenia.
Zespolenie obu materiałów pozostaje nienaruszone.
Współczynniki rozszerzalności liniowej betonu i stali są praktyczne jednakowe.
Naprężenia termiczne, nawet przy dużych różnicach temperatur są małe i nie wywołują szkodliwych odkształceń.
Beton doskonale chroni stal przed korozją i działaniem ognia
Stal ogranicza skutki skurczu betonu (zarysowania) oraz pełzania betonu (przyrost odkształceń).
ZALETY I WADY ŻELBETU
ZALETY:
ŁATWOŚĆ FORMOWANIA w dowolne kształty.
WYSOKA WYTRZYMAŁOŚĆ I TRWAŁOŚĆ konstrukcji, której czas eksploatacji w zależności od warunków atmosferycznych wynosi 60-150 lat.
SZTYWNOŚĆ KONSTRUKCJI MONOLITYCZNYCH
ogranicza stosowanie stężeń w płaskich układach prętowych, pozwala konstruować cienkie przekrycia o dużych rozpiętościach oraz układy przestrzenne.
OGNIOODPORNOŚĆ betonu zwykłego pozwala mu znosić okresowo temp. ok. 5000C, przy której odkryta stal traci 50% swojej wytrzymałości.
ODPORNOŚĆ NA WAHANIA TEMP. I WILGOCI oraz innych wpływów atmosferycznych.
TANIA KONSERWACJA szczelny beton chroni stal przed korozją i praktycznie nie wymaga konserwacji.
WADY:
POWSTAWANIE RYS I ODPRYSKÓW W BETONIE.
PRACOCHŁONNOŚĆ I SEZONOWOŚĆ, długi okres dojrzewania, konieczność starannej pielęgnacji.
DUŻE ZUŻYCIE DREWNA tylko w konstrukcjach monolitycznych gdy nie stosuje się deskowań do wielokrotnego użytku.
DUŻA PRZEWODNOŚĆ CIEPLNA I DŹWIĘKOWA
konieczność stosowania specjalnych izolacji termicznych i akustycznych.
ZNACZNY CIĘŻAR OBJĘTOŚCIOWY BETONU.
TRUDNOŚCI W PRZEPROWADZANIE ZMIAN I WZMOCNIEŃ.
BETON
WIADOMOŚCI OGÓLNE
Beton jest materiałem sztucznym powstałym po stwardnieniu mieszaniny, w skład której wchodzą:
kruszywo - naturalne lub sztuczne,
cement - najczęściej portlandzki,
woda - konieczna do wiązania cementu,
dodatki (do 5% masy cementu) lub domieszki specjalne (do 40% masy cementu),które np. przyspieszają twardnienie, umożliwiają betonowanie w niskich temperaturach
.
Beton należy do materiałów sprężysto-plastycznych o dużej niejednorodności i skomplikowanej strukturze.
Cechy fizyczne i mechaniczne betonu są zmienne w czasie i zależą od:
- wieku betonu,
- warunków cieplno-wilgotnościowych,
- czasu działania i wielkości obciążenia.
Cechy fizyczne to: skurcz i pełzanie, mrozoodporność i ognioodporność, itp.
Najistotniejsze cechy mechaniczne jak wytrzymałość i odkształcalność będą szczegółowo omówione.
Obecnie obowiązuje norma zharmonizowana z Eurokodem 2 :
PN-EN 206:2003 „Beton. Część 1
Wymagania, właściwości, produkcja i zgodność“
(zastąpiła ona normę PN-88/B-06250 „Beton zwykły”).
Betony stosowane w żelbecie podzielono w zależności od gęstości objętościowej:
Rodzaj betonu |
Symbol |
Gęstość objętościowa [kg/m3] |
Lekki |
LC |
800-2000 |
Zwykły |
C |
2000-2600 |
Ciężki |
C |
>2600 |
W konstrukcjach z betonu zbrojonego ilość stali jest niewielka.
Zbrojenie stanowi zazwyczaj 2-3% całkowitej objętości elementu.
W konstrukcji żelbetowej 95% objętości stanowi tworzywo betonowe.
Jakość konstrukcji żelbetowej zależy głównie od jakości betonu.
Z tego względu jakość betonu i jego właściwości są sprawą pierwszej wagi dla projektantów i wykonawców.
WYTRZYMAŁOŚĆ BETONU NA ŚCISKANIE
Za podstawę oceny jakości betonu przyjęto jego wytrzymałość na ściskanie.
Badanie tej wytrzymałości jest znormalizowane i opisane w normie „Beton zwykły” PN-88/B-06250.
Przy obliczaniu i wykonywaniu konstrukcji potrzebna jest znajomość różnych rodzajów wytrzymałości betonu na ściskanie:
gwarantowanej wytrzymałości betonu,
klasy betonu,
charakterystycznej wytrzymałości betonu na ściskanie,
obliczeniowej wytrzymałości betonu na ściskanie.
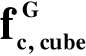
![]()
- wytrzymałość gwarantowana betonu
Wytrzymałość betonu na ściskanie mierzona
zgodnie z PN-88/B-06250 na kostkach sześciennych
o krawędzi 150 mm.
Gwarantowana przez producenta.
Prawdopodobieństwo wystąpienia wytrzymałości mniejszej niż gwarantowana jest ≤ 5%.
Podany w normie symbol np. B20 oznacza, że jest to
beton klasy 20, czyli o wytrzymałości gwarantowanej
równej 20 MPa.
-charakterystyczna wytrzymałość betonu
na ściskanie
Jest odpowiednikiem wytrzymałości gwarantowanej
w konstrukcji ( w jednoosiowym stanie naprężenia)
Określana :
na podstawie wytrzymałości gwarantowanej zgodnie ze wzorem fck=0,8 f
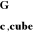
lubmierzona na walcach o średnicy 150 i wysokości 300 mm.
Prawdopodobieństwo wystąpienia wytrzymałości
mniejszej niż charakterystyczna jest ≤ 5%.
obliczeniowa wytrzymałość betonu
na ściskanie
Wytrzymałość przyjmowana przy sprawdzaniu
stanów granicznych konstrukcji.
Otrzymywana jest przez podzielenie wytrzymałości
charakterystycznej przez częściowy współczynnik
bezpieczeństwa dla betonu γc.
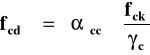
αcc - współczynnik
γc - częściowy współczynnik bezpieczeństwa
Współczynnik αcc można przyjmować
αcc = 1,0 |
(jeżeli norma nie ustanawia inaczej)
wyjątkiem
- elementów konstrukcyjnych o wyjątkowym znaczenie, których zniszczenie pociągnęłoby za sobą katastrofalne skutki społeczne i materialne, dla których zaleca się przyjmować
αcc = 0,85
- elementów ściskanych o małym przekroju poprzecznym
Ac ≤ 0,09 m2, gdy jeden z boków lub średnica przekroju są nie mniejsze niż 0,25 m, dla których
αcc oblicza się ze wzoru:
αcc = 0,85 dla 0,04 m2 ≤ Ac ≤ 0,09 m2
αcc = 0,85 Ac / 0,04 dla Ac < 0,04 m2
Częściowy współczynnik bezpieczeństwa γc zależy od sytuacji obliczeniowych:
- w sytuacjach trwałych i przejściowych:
γc = 1,5 dla konstrukcji żelbetowych i sprężonych
γc = 1,8 dla konstrukcji betonowych,
- w wyjątkowej sytuacji obliczeniowej:
γc = 1,3 dla konstrukcji żelbetowych i sprężonych
γc = 1,6 dla konstrukcji betonowych.
WYTRZYMAŁOŚĆ BETONU NA ŚCISKANIE
Wytrzymałość gwarantowana= klasa betonu |
Wytrzymałość charakterystyczna |
Wytrzymałość obliczeniowa |
|
fck |
fcd |
wieloosiowy stan naprężenia |
jednoosiowy stan naprężenia |
γc - współczynnik bezpieczeństwa w sytuacjach trwałych i przejściowych γc=1,5 konstr. żelbetowe γc=1,8 konstr. betonowe
|
B20 = 20 MPa |
fck = 16 MPa |
fcd = 10,6 MPa |
PRÓBKA |
KONSTRUKCJA |
BEZPIECZNE OBLICZENIA |
KLASY BETONU
W normie przyjęto 9 klas betonu (patrz tablica 2 normy).
Zrezygnowano z niskich klas betonu B7,5, B10, B12,5.
Wprowadzono wysokie klasy betonu B55, B60.
Klasy betonu
PN-B-03264:2002 |
B15 |
B20 |
B25 |
B30 |
B37 |
B45 |
B50 |
B55 |
B60 |
PN-B-03264:84 |
B7,5 |
B10 |
B12,5 |
B15 |
B17,5 |
B20 |
B25 |
B30 |
B35 |
B40 |
B50 |
Najniższe klasy betonu
dla poszczególnych rodzajów konstrukcji
Rodzaj konstrukcji |
Najniższa klasa betonu wg |
|
|
PN 2002 |
PN 1984 |
Konstrukcje betonowe |
B15 |
B7,5 |
Konstrukcje żelbetowe, stal A-0 i A-I |
B15 |
B10 |
Konstrukcje żelbetowe, stal A-II i A-III |
B15 |
B15 |
Konstrukcje żelbetowe, stal A-III N |
B20 |
B20 |
Usunięto niskie klasy betonu aby polepszyć jakość i trwałość konstrukcji.
Betony niskich klas są nadmiernie porowate i przepuszczają składniki powodujące korozję zbrojenia.
Dobry beton chroni skutecznie stal przed korozją.
Aktualna norma żelbetowa wprowadziła w grudniu 2004r poprawkę, która uwzględnia nowe oznaczenia klas betonu jakie znalazły się w normie PN-EN 206-1:2003 Beton-Część 1.
Poprawkę tą stanowi załącznik F.
Załącznik F (informacyjny)
RÓWNOWAŻNE OZNACZENIA KLAS BETONU LITERAMI B (podane w PN-88/B-06250) i C (podane w PN-EN 206-1:2003)
Tablica F.1 - Równoważne oznaczenia klas betonu
B15 B20 B25 B30 B37 B45 B50 B55 B60
C12/15 C16/20 C20/25 C25/30 C30/37 C35/45 C40/50 C45/55 C50/60
|
np. C20/25 oznacza beton, którego:
- minimalna wytrzymałość charakterystyczna = 20 MPa,
(oznaczona na próbkach walcowych o wymiarach 150/300 mm),
- wytrzymałość gwarantowana = 25 MPa
(oznaczona na kostkach sześciennych o boku 150 mm).
WYTRZYMAŁOŚĆ BETONU NA ROZCIĄGANIE
Doświadczalne określanie wytrzymałości betonu na rozciąganie sprawia wiele trudności.
Rozciąga się bezpośrednio próbki mocowane w prasie za pomocą specjalnych szczęk lub przyklejane do podkładek.
Badanie to nie zostało znormalizowane.
Wartość wytrzymałości betonu na rozciąganie zależy od klasy betonu, a więc od wytrzymałości na ściskanie.
Wytrzymałość betonu na rozciąganie określa się w praktyce z tabeli 2 w normie lub empirycznych wzorów przeliczeniowych.
Tabela 2 określa:
charakterystyczną wytrzymałość
betonu na rozciąganie fctk
obliczeniową wytrzymałość
betonu na rozciąganie fctd
średnią wytrzymałość
betonu na rozciąganie fctm
Wytrzymałość betonu na rozciąganie wynosi około 10% jego wytrzymałości na ściskanie.
|
ZMIENNOŚĆ WYTRZYMAŁOŚĆI W CZASIE
Wytrzymałość betonu z upływem czasu ulega wzrostowi w wyniku postępującego procesu twardnienia.
Tempo przyrostu wytrzymałości zależy od wielu czynników, z których największy wpływ mają:
rodzaj i ilość cementu na 1 m3 mieszanki,
warunki cieplno- wilgotnościowe.
W okresie początkowym przyrost wytrzymałości jest bardzo szybki a po 28 dniach staje się coraz wolniejszy.
Wzrost wytrzymałości betonu nieobciążonego może po 1 roku wynosić 30-75% wytrzymałości 28-dniowej.
W zależności od warunków dojrzewania i pielęgnacji beton może nie wykazywać wzrostu wytrzymałości.
W obliczeniach konstrukcji przyjmuje się zawsze 28-dniową wytrzymałość betonu.
ODKSZTAŁCALNOŚĆ BETONU
Element betonowy zmienia swoje wymiary, czyli odkształca się pod wpływem obciążenia.
Dodatkowo pojawiają się odkształcenia wywołane skurczem i pęcznieniem, pełzaniem, oraz zmianami temperatury.
Pod działaniem obciążeń powstają:
odkształcenia sprężyste oraz
odkształcenia plastyczne (trwałe).
Wykres zależności odkształceń σc do naprężeń εc określa się na podstawie badań próbek betonowych ściskanych osiowo lub rozciąganych aż do zniszczenia.
Kształt wykresu doświadczalnego pokazano na rys. a).
Badania wykonuje się sporadycznie W obliczeniach nośności przekroju korzystamy z paraboliczno-prostokątnego wykresu σ-ε podanego w normie, który pokazano na rys. b).
Wykres zależności c w betonie
a) zbadany doświadczalnie b) paraboliczno-prostokątny
przyjęty w normie
Analizując normowy wykres σ-ε widzimy, że w przedziale odkształceń εc= 0-2,0‰ wykres jest parabolą, natomiast dalej w przedziale εc= 2,0-3,5‰ wykres jest prostą (σc=const).
Podstawowym założeniem jest przyjęcie stałych wartości odkształcenia, które nie zależą od klasy beton:
εc= 2,0‰
εc= 3,5‰ (graniczne odkształcenie przy zniszczeniu).
Przy sprawdzaniu nośności przekrojów zginanych, mimośrodowo ściskanych i rozciąganych norma dopuszcza jak w poprzedniej wersji prostokątny wykres naprężeń.
MODUŁ SPRĘŻYSTOŚCI BETONU
Wartości modułu sprężystości Ec betonu określa się ze znanego warunku:
Ec= σc / εc
Z przebiegu wykresu σc = f(εc) pokazanego na rysunkach
widać, że dla betonu stosunek σc / εc nie przybiera wartości stałej.
Moduł sprężystości betonu jest wartością zmienna.
Praktyczne znaczenie ma tzw. średni moduł sprężystości Ecm.
Wartość Ecm wyrażona jest tangensem kąta αm nachylenia siecznej wyznaczonej w punkcie σ = 0,4 fck.
W tablicy 2 w normie zestawiono klasy i wytrzymałości betonu oraz odpowiadające im moduły sprężystości betonu Ecm.
Wartość modułu sprężystości zależy od klasy betonu i jest podana w normie w tablicy 2 normy.
|
SKURCZ BETONU
Dojrzewanie i twardnienie świeżego betonu w warunkach suchych powoduje zmniejszenie jego objętości zwane skurczem.
Jeżeli proces twardnienia betonu przebiega w wodzie, to występuje zjawisko odwrotne, zwane pęcznieniem.
Wartości skurczu i pęcznienia zależą od wieku i składu betonu, warunków cieplno-wilgotnościowych oraz wymiarów elementu.
Roczny skurcz betonu wynosi zwykle 0,2-0,5 mm/m,
w zaprawach cementowych dochodzi do 2 mm/m.
Przykładowo skurcz elementu o dł. = 6 m, może osiągnąć
0,5 mm/m · 6,0 m = 3,0 mm.
Skurcz ustaje z upływem czasu osiągając po około 3 latach końcową wartość odkształceń skurczowych εcs, którą można odczytać w tablicy B.1 w załączniku normy.
PEŁZANIE BETONU
Pełzanie betonu jest to przyrost odkształceń elementu pod działaniem długotrwałych stałych obciążeń.
Odkształcenia wywołane pełzaniem zależą od wielu czynników:
wieku betonu w chwili obciążenia
poziomu naprężeń ściskających w betonie σc
wilgotności względnej powietrza i wymiarów elementu
Proces pełzania może trwać wiele lat, z czasem maleje i zanika.
Odkształcenia εcc spowodowane pełzaniem pod wpływem naprężeń ściskających σc w przedziale czasu od t0 do t oblicza się ze wzoru:
w którym współczynnik pełzania φ(t, t0) zależy od poziomu naprężeń σc ściskających działających na element.
Wartości końcowego wspłóczynnika pełzania φ(∞, t0) zestawiono w tablicy A.1 w załączniku normy.
Pełzanie ma duży wpływ na ostateczne deformacje elementów z betonu. Wraz z upływem czasu następuje przyrost ugięć, szerokości rozwarcia rys oraz wzrost strat siły sprężającej w konstrukcjach sprężonych. Efekty spowodowane zjawiskiem pełzania betonu muszą być uwzględniane w obliczeniach konstrukcji.
WSPÓŁCZYNNIK LINIOWEJ ROZSZERZALNOŚCI TERMICZNEJ
Wartość współczynnika liniowej rozszerzalności termicznej betonu można przyjmować:
αt = 1 x 10 -5 / 0C
W przedziale najczęściej spotykanych temperatur, tj.
od -200C do +1000C, wartość ta nie odbiega od termicznej odkształcalności stali (1,2 x 10 -5 / 0C).
STAL ZBROJENIOWA
Zbrojenie konstrukcji żelbetowych stanowią na ogół pręty o przekroju okrągłym - gładkie lub profilowane.
Zbrojenie wykonuje się z pojedynczych prętów, gotowych siatek i szkieletów.
Do zbrojenia konstrukcji żelbetowych stosować należy pręty oraz druty o właściwościach mechanicznych określanych w normie PN- 82/H-93215 oraz inne stale pod warunkiem, że posiadają aktualną aprobatę techniczną.
Stal zbrojeniową, zależnie od jej właściwości mechanicznych zalicza się do odpowiedniej klasy stali.
Klasa stali to określenie własności mechanicznych
stali zbrojeniowych.
Rozróżnia się 5 klas stali: A-O, A-I, A-II, A-III, A-IIIN.
Pręty ze stali klasy A-0 i A-I są gładkie i wymagają na ogół zakończeń hakowych ( dla zwiększenia przyczepności w strefie zakotwienia).
Pręty klasy A-II, A-III, A-IIIN są żebrowane, mają dobrą przyczepność do betonu i można je stosować bez zakończeń hakowych.
Klasie stali przypisane są :
znak gatunku stali,
nominalna średnica prętów Φ [mm],
charakterystyczna granica plastyczności fyk,
obliczeniowa granica plastyczności fyd,
wytrzymałość charakterystyczna na zerwanie ftk.
Wartości fyk, fyd, ftk podane są w tablicy 3 w normie.
Stale żebrowane mają zróżnicowany układ żeberek, ułatwia to rozpoznanie poszczególnych gatunków stali.
Pręty ze stali klasy A-II żebrowane są spiralnie (rys a,b),
natomiast klasy A-III i A-IIIN w jodełkę (rys c,d).
Rysunek2.15 str 84 Łapko
Stale żebrowane
a) A-II gatunek 18G2 b) A-II gatunek St50B
c)A-III gatunek 34GS d) A-IIIN gatunek 20G2VY
Zgodnie z wytycznymi Instytutu Techniki Budowlanej podstawowym gatunkiem stali do wykonywania zbrojenia nośnego konstrukcji jest stal klasy A-III, gatunek 34G S.
Stal ta nie może być stosowana w elementach obciążonych dynamicznie, dopuszcza się stosowanie w przypadku obciążeń wielokrotnie zmiennych.
W krajach Unii Europejskiej powszechnie stosowana jest stal żebrowana gatunku B500, która ma granicę plastyczności powyżej 500 MPa.
Polskie huty produkują także stal o podwyższonej wytrzymałości gatunku RB500W oraz BSt500S i posiadają dla tych wyrobów odpowiednie aprobaty techniczne.
ODKSZTAŁCALNOŚĆ STALI ZBROJENIOWEJ
Badanie próbki stali poddanej działaniu siły rozciągającej
pozwala określić wykres zależności σ-ε, a także granicę plastyczności i moduł sprężystości.
Norma dopuszcza przyjmowanie do obliczeń wykresu σ-ε stali w postaci uproszczonej z poziomą półką (patrz rys).
Wykres σ-ε stali zbrojeniowej
W założeniach obliczeniowych ogranicza się odkształcenia prętów zbrojenia εuk do 10‰.
Moduł sprężystości stali Es wynosi 200 000 MPa.
RODZAJE ZBROJENIA
Zbrojenie konstrukcji żelbetowych w zależności od pełnionej funkcji dzieli się na:
nośne ,
montażowe,
rozdzielcze.
Przekrój zbrojenia nośnego, nazywanego też głównym lub konstrukcyjnym określa się na podstawie obliczeń.
Przekrój zbrojenia montażowego i rozdzielczego nie jest obliczany, lecz przyjmowany na podstawie warunków normowych.
Zbrojenie dostarczane jest na budowę w kręgach (małe średnice) oraz w postaci prętów prostych o długości do 12m. Większe długości można otrzymać tylko w uzgodnieniu z producentem.
KSZTAŁT ZBROJENIA
Pręty proste
Pręty rozciągane gładkie (klasy A-0, A-I) można kończyć hakiem półokrąglym, pręty żebrowane (klasy A-II, A-III, A-IIIN) kończy się bez haka, hakiem prostym lub pętlą.
Pręty ściskane, niezależnie od klasy stali kończy się bez haka.
Siatki zbrojeniowe
a) płaska b) zwinięta w rulon
Szkielety zbrojeniowe
WYMIAROWANIE PRZEKROJÓW ŻELBETOWYCH METODĄ STANÓW GRANICZNYCH
Wymiarowanie polega na określeniu optymalnego i bezpiecznego przekroju betonu i stali w chwili osiągnięcia przez element stanu granicznego.
Przyjęta w normie PN-B-03264 zasada wymiarowania konstrukcji żelbetowych opiera się na metodzie stanów granicznych.
Stan graniczny zostaje osiągnięty jeżeli konstrukcja lub jej część przestaje odpowiadać założonym wymaganiom realizacji lub użytkowania.
Stany graniczne dzielone są na dwie grupy:
stany graniczne nośności odpowiadające maksymalnej nośności konstrukcji,
stany graniczne użytkowalności ustalone na podstawie kryteriów związanych z eksploatacją i trwałością konstrukcji.
Stany graniczne nośności
Osiągnięcie stanu granicznego nośności oznacza awarię lub taką formę uszkodzeń, które zagrażają życiu ludzkiemu.
Sprawdzenie stanu granicznego nośności polega na wykazaniu, że:
Sd ≤Rd
gdzie:
Sd - obliczeniowy moment lub siła przekrojowa,
Rd - obliczeniowa nośność elementu, przy
założeniu obliczeniowych wytrzymałości
betonu i stali.
Licząc nośność używamy:
obliczeniowych obciążeń Fd = γf Fk
gdzie: γf -częściowy współczynnik bezpieczeństwa dla rozpatrywanych obciążeń,
obliczeniowych wytrzymałości materiałów fd =![]()
gdzie: γm -częściowy materiałowy współczynnik bezpieczeństwa
Stany graniczne użytkowalności
Stany graniczne użytkowalności obejmują sytuacje, w których konstrukcja staje się nieprzydatna do normalnej eksploatacji.
Do stanów granicznych użytkowalności należą:
stan graniczny ugięć,
stan graniczny zarysowania,
stan graniczny naprężeń (tylko dla konstrukcji sprężonych).
Licząc ugięcie lub zarysowanie używamy:
obciążeń charakterystycznych Fk,
średnich wytrzymałości i modułów sprężystości
materiałów.
ELEMENTY ZGINANE
Ustroje prętowe, płytowe lub tarczowe, którymi w praktyce są belki oraz płyty to typowe przykłady elementów zginanych.
W żelbetowych elementach zginanych, po przekroczeniu naprężeń w strefie rozciąganej, pojawią się rysy prostopadłe do osi elementu.
Mogą też pojawić się rysy ukośne na odcinkach przy podporach lub w okolicy przyłożenia siły skupionej.
W związku z tym obliczanie nośności elementów zginanych - zwłaszcza belek przeprowadza się w dwóch etapach:
na zginanie, czyli oddziałanie momentów zginających,
na ścinanie, czyli oddziaływanie sił poprzecznych
(omówione w dalszym rozdziale).
Żelbetowa belka wolnopodparta, równomiernie obciążona:
obraz zarysowania,
wykres momentów zginających i sił poprzecznych.
FAZY NAPRĘŻEŃ W BELCE ZGINANEJ
Rozpatrzmy zachowanie się żelbetowej belki jednoprzęsłowej, swobodnie podpartej, obciążonej siłą skupioną (pomijamy wpływ ścinania).
W belce poddanej działaniu momentu zginającego powstają naprężenia normalne pochodzące od zginania:
naprężenia ściskające - powyżej osi obojętnej,
naprężenia rozciągające - poniżej osi w tzw. strefie rozciąganej.
Prostoliniowy wykres momentów ma wartość zerową przy podporze, zaś w środku elementu maksymalną.
Analizując poszczególne przekroje belki zauważamy, że naprężenia w nich występujące wzrastają proporcjonalnie ze wzrostem momentu.
Na długości belki obserwujemy różne rozkłady naprężeń zwane potocznie fazami wytężenia elementu żelbetowego:
w fazie I pracują przekroje niezarysowane,
faza II obejmuje przekroje zarysowane,
faza III odpowiada stadium osiągnięcia nośności.
faza Ia
Wartość momentu jest niewielka.
Wykres naprężeń jest liniowy na całej wysokości przekroju.
faza Ib
Wartość momentu wzrasta.
Wykres naprężeń w strefie ściskanej jest nadal prostoliniowy.
Nastąpiło uplastycznienie betonu strefy rozciąganej (wykres naprężeń krzywoliniowy).
Faza tuż przed pojawieniem się rysy.
Na rysunku można zauważyć, że w przekrojach między rysami belka zachowuje się jak w fazie I. Oznacza to, że beton rozciągany nadal współpracuje tam ze zbrojeniem.
faza IIa
Po zarysowaniu betonu całość sił rozciągających przejmuje zbrojenie.
W strefie ściskanej rozkład naprężeń w betonie jest nadal prostoliniowy.
faza IIb
Zasięg rys jest coraz większy.
Wykres naprężeń na wysokości strefy ściskanej jest wyraźnie krzywoliniowy.
faza III
Faza zniszczenia (wyczerpania nośności)
Zniszczenie może nastąpić w wyniku wyczerpania nośności strefy ściskanej
(ang. compression failure)
Naprężenie w betonie jest równe jego wytrzymałości na ściskanie.
Zniszczeniu może ulec strefa rozciągana - gdy naprężenie w zbrojeniu osiągnie granicę plastyczności
(ang. tension failure).
Zachowanie się przekroju w fazie III i związany z nią rozkład naprężeń jest podstawą do wymiarowania elementów w stanie granicznym nośności w normie PN-99 (oraz wszystkich normach począwszy od 1956 r).
Norma wprowadza uproszczenie polegające na zamianie krzywoliniowego wykresu naprężeń w betonie strefy ściskanej na wykres prostokątny.
STAN GRANICZNY NOŚNOŚCI
ZGINANYCH ELEMENTÓW ŻELBETOWYCH
Sprawdzenie stanu granicznego nośności polega na wykazaniu, że w każdym przekroju belki lub płyty zginanej spełniony jest warunek
MSd ≤ MRd
MSd - moment od obciążeń obliczeniowych,
MRd - nośność obliczeniowa przekroju na zginanie.
Zasady ogólne
Nośność elementów zginanych, (a także ściskanych i rozciąganych) określa się z warunków równowagi sił wewnętrznych w przekroju, przyjmując następujące założenia:
przekroje płaskie przed odkształceniem pozostają płaskimi po odkształceniu (zasada Bernoulliego),
wytrzymałość betonu na rozciąganie jest pomijana (przekrój jest zarysowany),
naprężenia w betonie ściskanym i stali określa się na podstawie zależności σ-ε przyjętych poprzednio,
Zależności σ-ε zalecane przy projektowaniu
a) dla betonu b) dla stali zbrojeniowej
stan graniczny nośności występuje, gdy spełniony będzie przynajmniej jeden z poniższych warunków:
odkształcenia w skrajnym włóknie ściskanym betonu osiągną wartość graniczną 3,5 ‰,
odkształcenia w zbrojeniu rozciąganym osiągną wartość graniczną - 10 ‰.
Metody obliczeń
Zgodnie z normą żelbetowy przekrój zginany można obliczać dwiema metodami: ogólną i uproszczoną.
W metodzie ogólnej przyjmuje się paraboliczno-prostokątny wykres naprężeń w betonie strefy ściskanej.
W metodzie uproszczonej przyjmuje się prostokątny wykres naprężeń w betonie strefy ściskanej.
W większości przypadków obie metody prowadzą do identycznych wyników końcowych.
W praktyce - ze względu na prostotę obliczeń -stosuje się metodę uproszczoną.
ODKSZTAŁCENIA I NAPRĘŻENIA W PRZEKROJU
odpowiadające granicznej wysokości strefy ściskanej xlim
OBLICZANIE ELEMENTÓW ZGINANYCH
METODĄ UPROSZCZONĄ
W metodzie uproszczonej nośność elementów zginanych oblicza się z warunku równowagi sił wewnętrznych.
Uproszczenie polega na przyjęciu prostokątnego wykresu naprężeń w strefie ściskanej.
Ekwiwalentny prostokątny wykres naprężeń ma zredukowany zasięg wysokości strefy ściskanej xeff do wartości
xeff = 0,8 x
Przy wymiarowaniu przekrojów potrzebny będzie bezwymiarowy parametr ξeff - zwany względną wysokością strefy ściskanej.
![]()
rysunek
Graniczną wartość względnej wysokości strefy ściskanej przekroju ξeff,lim ustala się na podstawie stanu odkształceń.
Wielkość ta wynika z przyjęcia granicznych odkształceń w betonie εc = 3,5 ‰ oraz odkształceń w zbrojeniu rozciąganym εyd = - fyd / Es .
Wartości ξeff,lim (wynikające z powyższego wzoru)
dla różnych klas stali podano w tablicy 9 normie.
Klasa stali |
ξeff,lim |
A-0 |
0,63 |
A-I |
0,62 |
A-II |
0,55 |
A-III |
0,53 |
A-IIIN |
0,50 |
Założenia do metody uproszczonej :
wytrzymałość betonu na rozciąganie jest pomijana,
wykres naprężeń σc w strefie ściskanej betonu ma kształt prostokąta,
w stanie granicznym nośności naprężenie σc nie może
przekraczać wartości obliczeniowej wytrzymałości
betonu na ściskanie fcd,
ekwiwalentny prostokątny wykres naprężeń ma zredukowany zasięg wysokości strefy ściskanej do wartości xeff = 0,8 x,
w obliczeniach elementów zginanych (a także ściskanych i rozciąganych) ogranicza się efektywną wysokość strefy ściskanej przekroju do wartości granicznej
xeff,lim = ξeff,lim d ;
gdzie graniczną wartość względnej wysokości strefy ściskanej przekroju ξeff,lim
wyznacza się ze wzoru
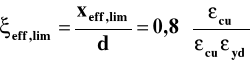
w którym:
εcu = 0,0035 graniczne odkształcenie betonu w strefie ściskanej przekroju,
εs = εyd = - fyd / Es odkształcenie stali, odpowiadające obliczeniowe granicy plastyczności stali fyd.
Graniczne wartości ξeff,lim dla stosowanych stali zbrojeniowych wg tablicy 9 normy
Klasa stali |
ξeff,lim |
A-0 |
0,63 |
A-I |
0,62 |
A-II |
0,55 |
A-III |
0,53 |
A-IIIN |
0,50 |
ZGINANIE- metoda uproszczona
PRZEKRÓJ PROSTOKĄTNY POJEDYŃCZO ZBROJONY
W przekroju zginanym obciążonym obliczeniowym momentem zginającym MSd powstają siły wewnętrzne Fc oraz Fs , które pozostają w równowadze.
Schemat do obliczania nośności
zginanego przekroju pojedyńczo zbrojonego
h,b - wysokość i szerokość belki
d - wysokość użyteczna przekroju (odległość od krawędzi ściskanej do środka ciężkości zbrojenia rozciąganego)
xeff - wysokość efektywna strefy ściskanej przekroju
z - ramię sił wewnętrznych
a1 - odległość środka ciężkości zbrojenia As1 od krawędzi rozciąganej
As1 - pole przekroju zbrojenia rozciąganego
Acc,eff - efektywne pole przekroju betonu strefy ściskanej (xeff * b)
MSd - moment zginający wywołany obciążeniem obliczeniowym
MRd - nośność obliczeniowa przekroju na zginanie
fcd - wytrzymałość obliczeniowa betonu na ściskanie
fyd - obliczeniowa granica plastyczności stali zbrojeniowej
Fc- wypadkowa naprężeń w strefie ściskanej betonu
położona w środku ciężkości bryły naprężeń
Fc = fcd Acc,eff = fcd b xeff
Fs- wypadkowa sił w zbrojeniu rozciąganym
Fs = fyd As1
Z rysunku wynika, że stan graniczny nośności wystąpi gdy osiągnięty zostanie przynajmniej jeden warunek:
naprężenia w betonie osiągną obliczeniową wytrzymałość betonu na ściskanie α fcd ,
naprężenia w stali osiągną obliczeniową granicę plastyczności stali fyd .
Nośność elementów zginanych oblicza się z warunków równowagi
momentów i sił.
Moment sił wewnętrznych wynikający z istnienia pary sił Fc i Fs1,
działających na ramieniu z = d - 0,5xeff ma postać:
MSd = Fc z = fcd b xeff (d - 0,5xeff )
lub
MSd = Fs1 z = fyd As1 (d - 0,5xeff )
Mamy też warunek równowagi sił:
Fc = Fs1
czyli
fcd b xeff = fyd As1
Niewiadome: xeff - efektywna wysokość strefy ściskanej
As1 - pole przekroju zbrojenia rozciąganego
W celu ułatwienia wymiarowania opracowane zostały tablice współczynników pomocniczych: ξeff , ζeff , μeff
ξeff = xeff / d
ζeff = z / d
μeff = ξeff · ζeff
Wyprowadzenie wzoru na nośność przekroju z warunku równowagi momentów:
MSd = Fc z = fcd xeff b (d - 0,5xeff )
podstawiamy xeff = ξeff d
MSd = fcd ξeff d b (d - 0,5 ξeff d)
po wyłączeniu d przed nawias i uporządkowaniu
MSd = fcd b d2 ξeff (1 - 0,5 ξeff )
ponieważ ξeff (1 - 0,5 ξeff ) = μeff
Nośność elementu zginanego obliczamy ze wzoru:
MSd = μeff fcd b d2
Wyprowadzenie wzoru na przekrój zbrojenia rozciąganego As1 z warunku równowagi momentów:
MSd = Fs1 z = fyd As1 (d - 0,5xeff )
po wyłączeniu d przed nawias
MSd = fyd As1 d (1 - 0,5xeff / d)
oraz podstawieniu ξeff = xeff / d
MSd = fyd As1 d (1 - 0,5ξeff )
ponieważ ζeff = (1 - 0,5ξeff) )
MSd = fyd As1 d ζeff
ostatecznie mamy wzór na przekrój zbrojenia
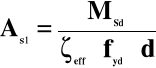
Algorytm do obliczania zbrojenia
rozciąganego w belce zginanej
DANE:
Materiały:
Beton np. B30, fcd = 16,7 MPa
Stal np. A II, fyd = 310 MPa
Obciążenie:
MSd - moment zginający wywołany obciążeniem obliczeniowym
Wymiary przekroju:
h - wysokość, b - szerokość,
d - użyteczna wysokość przekroju,
a1 - odległość środka ciężkości zbrojenia As1 od krawędzi rozciąganej
SZUKANE:
As1 - przekrój zbrojenia rozciąganego
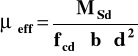
μ lim = ξ eff,lim (1 - 0,5 ξ eff,lim) ξ eff,lim - z tablicy 9
jeżeli μ eff < μ lim - przekrój pojedynczo zbrojony
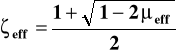
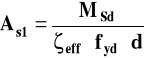
PRZEKRÓJ TEOWY
POJEDYŃCZO ZBROJONY
W konstrukcjach monolitycznych płyta opierając się na żebrach współpracuje z nimi. Oba elementy tworzą łącznie przekrój w kształcie litery T - zwany teowym.
Współpraca płyty z żebrem może być uwzględniana w obliczeniach tylko wtedy gdy płyta znajduje się w strefie ściskanej.
W obszarze momentów ujemnych - rozciągających płytę może ona ulec zarysowaniu i tam nie uwzględnia się współpracy z żebrem.
Płyty w stropach monolitycznych liczone są jako belki ciągłe.
Analizując wykres momentów zginających w takiej belce widzimy że:
w przekrojach przęsłowych płyta jest ściskana więc belka może mieć przekrój teowy,
w przekrojach podporowych płyta jest rozciągana więc belka ma w obliczeniach przekrój prostokąta
( nie uwzględnia się współpracy z płytą).
Określenie efektywnej szerokości półki beff
w przekrojach teowych
Szerokość półki beff jest stała na całej długości przęsła, na której występuje moment jednakowego znaku.
bw - szerokość środnika
Szerokość beff w obliczeniach ograniczają warunki:
dla przekrojów symetrycznych
beff = bw + l0 / 5 ≤ bw + b1 + b2
dla przekrojów z półką jednostronną
beff = bw + l0 / 10 ≤ bw + b1
Wartość l0 między punktami zerowych momentów przyjmować należy zgodnie z poniższym rysunkiem.
przy sprawdzaniu stanu granicznego nośności należy ponadto sprawdzić, czy:
beff1 lub beff2 ≤ 6 hf - w przekrojach symetrycznych
beff1 lub beff2 ≤ 4 hf - w przekrojach z półką jednostronną.
WYMIAROWANIE PRZEKROJU TEOWEGO
O sposobie wymiarowania belki teowej decyduje kształt strefy ściskanej przekroju.
Wyróżnia się dwa przypadki obliczeniowe w zależności od położenia osi obojętnej.
PRZEKRÓJ POZORNIE TEOWY
Oś obojętna znajduje się w półce, strefa ściskana ma kształt prostokąta, ponieważ
xeff ≤ hf
Beton w strefie rozciąganej nie pracuje, przekrój można więc traktować jako prostokąt o wymiarach beff • h .
Przekrój nazywa się pozornie teowy, bo jest liczony tak jak prostokąt.
Nośność przekroju określa wzór jak dla prostokąta
MSd = Fc z = fcd beff xeff (d - 0,5xeff )
lub
MSd = Fs1 z = fyd As1 (d - 0,5xeff )
Algorytm wymiarowania przekroju o kształcie teowym jest taki sam jak przekroju prostokątnego'
jeżeli ξeff ≤ ξeff ,lim - przekrój pojedynczo zbrojony
|
PRZEKRÓJ RZECZYWIŚCIE TEOWY
Oś obojętna znajduje się w środniku, strefa ściskana ma kształt teowy, ponieważ
xeff > hf
Strefa ściskana ma kształt teowy tylko wtedy, gdy na przekrój działają bardzo duże obciążenia
Omawiany przypadek, występuje w praktyce stosunkowo rzadko.
PRZEKRÓJ PROSTOKĄTNY
PODWÓJNIE ZBROJONY
Przekrój prostokątny należy zbroić podwójnie jeżeli
ξeff > ξeff, lim
Przypadek ten zdarza się gdy na przekrój działa bardzo duży moment.
Strefa ściskana jest wtedy duża ( xeff > xeff, lim ), konieczne jest jej wzmocnienie dodatkowym zbrojeniem As2.
Bez zbrojenia dodatkowego strefa ściskana zniszczy się zanim zostanie osiągnięta nośność w zbrojeniu rozciąganym.
Jeżeli nie można zwiększyć wymiarów przekroju elementu, to trzeba wprowadzić dodatkowe zbrojenie w strefie ściskanej As2 .
Przekrój taki nazywamy podwójnie zbrojonym,
ponieważ posiada zbrojenie rozciągane As1 oraz zbrojenie ściskane As2
Schemat sił do obliczania nośności
zginanego przekroju podwójnie zbrojonego
W praktycznym wymiarowaniu informację, że przekrój należy zbroić podwójnie otrzymujemy gdy okaże się w obliczeniach, że
![]()
> Ao,,lim
PRZEKRÓJ TEOWY
PODWÓJNIE ZBROJONY
Przekrój teowy należy zbroić podwójnie jeżeli
ξeff > ξeff, lim
Przypadek ten, podobnie jak dla prostokąta, zdarza się gdy na przekrój działa bardzo duży moment.
W praktyce unika się takich rozwiązań, ze względu na znaczne zużycie zbrojenia.
WSTĘPNE PRZYJĘCIE WYMIAROW BELKI
Ze względu na stan graniczny nośności
Dane:
obciążenie obliczeniowe (g+q),
rozpiętość obliczeniowa przęsła belki leff ,
moment od obciążeń obliczeniowych obliczony szacunkowo jak dla belki wolnopodpartej
M0 =
w przypadku schematu belki ciągłej wieloprzęsłowej
redukujemy moment przyjmując -
M = 0,7 M0
Przyjęto:
klasę betonu np. B25 fcd = 13,3 MPa
klasę stali np A-II fyd = 310 MPa
stopień zbrojenia ρ = 1 %
szerokość belki b = ..............
Obliczenie wysokości belki:
ξ = ρ = 0,01
A0 = ξ ( 1 - 0,5 ξ )
d =
Ze względu na stan graniczny ugięć
Tablica 15 w normie podaje maksymalną wartość stosunku rozpiętości leff do wysokości użytecznej d , przy której można nie sprawdzać ugięć,
Np.- dla skrajnego przęsła belki ciągłej,
- stopnia zbrojenia As / b d = 1%,
- betonu klasy B 25
= 22
a więc d =
Uwaga!
Dla elementów o rozpiętości leff > 6,0m maksymalne wartości stosunku leff / d podane w tablicy 15 należy pomnożyć przez:
200 - w przypadku stropów i stropodachów,
150 - w przypadku przekryć dachowych.
gdzie: alim - ugięcie graniczne wg tab. 10
ŚCINANIE ELEMENTÓW ŻELBETOWYCH
Nośność belki żelbetowej sprowadza się oddzielnie na:
działanie momentu zginającego (w przekroju prostopadłym do osi),
działanie siły poprzecznej (w przekroju ukośnym do osi).
Ścinanie występuje głównie w strefach przypodporowych gdzie siła poprzeczna jest największa oraz w miejscach przyłożenia sił skupionych.
W belce żelbetowej oblicza się:
zbrojenia podłużnego związane z działaniem momentu zginającego (w obszarach rys prostopadłych).
zbrojenie poprzeczne związane z działaniem sił porzecznych (w obszarach rys ukośnych).
W chwili powstania rys ukośnych naprężenia wywołane
ścinaniem przenoszone są przez zbrojenie poprzeczne
czyli -strzemiona i pręty odgięte,
(pręty podłużne i beton ściskany przenoszą ścinanie w niewielkim stopniu).
Zbrojenie na ścinanie w belce żelbetowej
Przedstawiona w obecnej normie metoda obliczania ścinania opiera się na modelu kratownicy opracowanym przez E. Mörscha (1929r.).
Na podstawie tzw. analogii kratownicowej zakłada się, że w belce wyróżniamy:
pas ściskany, - który stanowi beton strefy ściskanej,
pas rozciągany, - który stanowi zbrojenie podłużne w strefie rozciąganej,
strefę ścinania, która położona jest pomiędzy wypadkowymi sił Fc oraz Fs
Wysokość strefy ścinania jest równa ramieniu sił wewnętrznych z.
Model kratownicy do obliczania ścinania belki
Fc - siła ściskająca w betonie ,
Fs - siła rozciągająca w zbrojeniu podłużnym,
z - ramię sił wewnętrznych
Strefa ścinania składa się z:
betonowych krzyżulców ściskanych nachylonych pod kątem θ do osi elementu (modelujących ukośne siły ściskające przenoszone przez beton).
krzyżulców rozciąganych nachylonych pod
kątem α (są one modelem zbrojenia poprzecznego),
Kąt θ nachylenia krzyżulców betonowych może przybierać dowolne wartości z przedziału:
1,0 ≤ ctgθ ≤ 2,0
26,60 ≤ θ ≤ 45,00
Kąt α nachylenia zbrojenia poprzecznego uwzględnianego w obliczeniach nie może być mniejszy niż 450.
W najprostszym przypadku jeżeli zbrojenie belki składa się wyłącznie ze zbrojenia podłużnego oraz strzemion analogia kratownicowa wygląda następująco:
Krzyżulce ukośne to beton ściskany.
Pionowe słupki rozciągane to strzemiona.
W tym schemacie można łatwo wyliczyć siły w zbrojeniu i betonie.
Powierzchnię strzemion wyliczamy zakładając, że przejmują one całą siłę poprzeczną V.
Sytuacja komplikuje się gdy chcemy jednocześnie uwzględnić pręty odgięte, strzemiona i beton.
Kratownica staje się statycznie niewyznaczalna i stopień wykorzystania któregoś z elementów trzeba założyć.
Graniczne siły poprzeczne
Obliczeniowa nośność na ścinanie VRd jest równa jednej z trzech granicznych sił poprzecznych:
VRd1, VRd2 albo VRd2, red, VRd3.
VRd1 - jest graniczną siłą poprzeczną w elemencie bez zbrojenia poprzecznego
VRd2 - jest graniczną siłą poprzeczną w betonowych krzyżulcach ściskanych
VRd2, red - jest graniczną siłą poprzeczną jak VRd2, ale w elementach mimośrodowo ściskanych
VRd3 - jest graniczną siłą poprzeczną w krzyżulcach rozciąganych
ZBROJENIE PODŁUŻNE W PASIE ROZCIĄGNYM
Analogia kratownicowa ma sens tylko wtedy jeżeli zbrojenie rozciągane w strefie działania sił poprzecznych jest w stanie przenieść siłę Fs =Td.
Zbrojenie to musi być odpowiednio zakotwione.
Powiększamy więc zasięg zbrojenia podłużnego w strefie ścinania rozsuwając obwiednię momentów o poziomy odcinek al.
W normie PN mamy:
al = 0,5 z ctgθ
![]()
Graniczna siła poprzeczna VRd1
![]()
bw - szerokość belki
k - współczynnik równy 1,0 gdy do podpory doprowadzono mniej niż 50% rozciąganego zbrojenia przęsłowego, a w innych przypadkach wyznaczony ze wzoru
k = 1,6 - d ≥ 1,0
τRd - obliczeniowa wytrzymałość betonu na ścinanie wyznaczona z tabl. 13
ρL - stopień zbrojenia wyznaczony ze wzoru
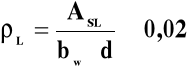
ASL - pole przekroju głównego zbrojenia rozciąganego mającego długość nie mniejszą niż d + lb,net poza rozpatrywanym przekrojem elementu
σcp - naprężenie w elementach obciążonych siłą podłużna i sprężonych
σcp = 0
Przypadki obliczeniowe przy projektowaniu przekrojów na ścinanie
Tok obliczania zbrojenia poprzecznego na ścinanie w belce wolnopodpartej o rozpiętości przęsła leff , równomiernie obciążonej obciążeniem ( g + q)
- Sprawdzenie czy obliczenie ścinania jest konieczne
Jeżeli VSd ≤ VRd1,
|
to nie trzeba liczyć ścinania. Odcinki na których spełniony jest ten warunek nazywa się odcinkami pierwszego rodzaju.
|
|
Jeżeli VRd1 < VSd ≤ VRd2, |
to konieczne jest obliczenie nośności przekrojów ukośnych na odcinkach określonych jako odcinki drugiego rodzaju.
|
|
Jeżeli VSd > VRd2, |
to przekrój nie może być prawidłowo zaprojektowany. Beton w krzyżulcach ściskanych ulega zmiażdżeniu, zmienić wymiary przekroju lub klasę betonu. |
|
Graniczne siły poprzeczne:
VRd1 - siła przenoszona przez „sam beton”,
VRd2 - graniczna siła w betonowych krzyżulcach ściskanych,
VRd3 - graniczna siła w krzyżulcach rozciąganych tj. w zbrojeniu
poprzecznym
![]()
bw - szerokość belki
k - współczynnik równy 1,0 gdy do podpory doprowadzono mniej niż 50% rozciąganego zbrojenia przęsłowego, a w innych przypadkach wyznaczony ze wzoru
k = 1,6 - d ≥ 1,0
τRd - obliczeniowa wytrzymałość betonu na ścinanie wyznaczona z tabl. 13
ρL - stopień zbrojenia wyznaczony ze wzoru
![]()
ASL - pole przekroju głównego zbrojenia rozciąganego mającego długość nie mniejszą niż d + lb,net poza rozpatrywanym przekrojem elementu,
σcp - naprężenie w elementach obciążonych siłą podłużna i sprężonych
σcp = 0
Okazało się, że trzeba liczyć ścinanie ponieważ:
VSd > VRd1
Vsd -obliczeniowa siła poprzeczna na podporze
Konieczne jest obliczenie dodatkowego zbrojenia poprzecznego na odcinku drugiego rodzaju o długości:
![]()
Przyjęto, że zbrojenie na ścinanie składa się wyłącznie ze strzemion prostopadłych do osi belki wtedy siłę VRd2 oblicza się ze wzoru:
gdzie:
ν = 0,7-fck/200
z - ramię sił wewnętrznych z = 0,9⋅d
ctgθ = 1,0 - 2,0
Maksymalny odstęp strzemion smax w kierunku podłużnym określają następujące warunki:
jeżeli VSd ≤ VRd2, smax = 0,8⋅d ≤ 300 mm
jeżeli , smax = 0,6⋅d ≤ 300 mm
jeżeli , smax = 0,3⋅d ≤ 200 mm
Założono zbrojenie samymi strzemionami
Graniczna siła w rozciąganym krzyżulcu
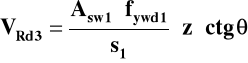
gdzie:
Asw1 - pole przekroju poprzecznego prętów tworzących jedno
strzemię, np. pole 4 prętów φ 6 dla strzemion podwójnych,
fywd1 - obliczeniowa granica plastyczności strzemion,
s1 - rozstaw strzemion,
θ - kąt nachylenia krzyżulców betonowych
1,0 ≤ ctgθ ≤ 2,0
Rozstaw strzemion potrzebny na odcinku drugiego rodzaju lt
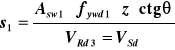
Stopień zbrojenia strzemionami ρw
![]()
Minimalny stopień zbrojenia strzemionami na ścinanie wg tabl. 32 wynosi
ρw min = 0,0014
ELELEMENTY ŚCISKANIE MIMOŚRODOWO
Typowe elementy ściskane to słupy, a także ściany i tarcze.
W praktyce, podłużna siła ściskająca działa na element na pewnym mimośrodzie. Oddziaływanie osiowe przyjmowane jest jedynie w założeniach teoretycznych.
Problematyka ściskania jest więc bardzo zróżnicowana.
Obejmuje ona przypadki tzw. „osiowego ściskania” gdzie mimośród statyczny ee=0 oraz przypadki gdzie ee→∞.
Rozkłady naprężeń w elemencie ściskanym (słupie), które zależą od wielkości mimośrodu pokazano na rysunku.
Przypadek ee=0 pokazany na rys a) to osiowe ściskanie, dające równomierny rozkład naprężeń w przekroju słupa.
Oddziaływanie siły na niewielkim mimośrodzie (w rdzeniu przekroju) powoduje nierównomierny trapezowy rozkład naprężeń - rys b).
Dalszy wzrost mimośrodu powoduje, że w przekroju pojawiają się naprężenia rozciągające rys c).
W przypadku działania siły na bardzo dużym mimośrodzie słup pracuje jak element zginany.
W obliczeniach słupa należy określić następujące mimośrody:
mimośród statyczny ee = MSd / NSd ,
gdzie: MSd i NSd to obliczeniowy moment i siła,
mimośród niezamierzony przypadkowy ea
Wartość niezamierzonego mimośrodu przypadkowego ea należy przyjmować równą największej z podanych w
normie warunków:
- w ustrojach monolitycznych, płytach i powłokach
ea= 10 mm,
- w elementach prefabrykowanych, z wyjątkiem płyt i
powłok ea= 20 mm,
- we wszystkich elementach o wysokości przekroju
poprzecznego ea= h/30,
- w ustrojach szkieletowych i tarczach o węzłach
nieprzesuwnych ea= lcol /600,
- w ustrojach szkieletowych o węzłach przesuwnych
dla elementów n-tej kondygnacji licząc od góry
ea= lcol (1+1/n ) /600.
Mimośród początkowy e0
Ostatecznie do obliczeń przyjmuje się mimośród początkowy e0, który jest sumą mimośrodu statycznego i niezamierzonego, czyli:
e0 = ee + ea
Długość obliczeniowa słupów l0
Obliczeniową długość słupów l0 wyznaczać można według zasad mechaniki budowli jak dla elementów z materiału liniowo sprężystego ze znanego wzoru:
l0 = ψ*l
ψ - współcz. wyboczeniowy
uwzględniający wpływ sposobu podparcia
słupa na końcach.
W normie wprowadzono inne oznaczenia ale sens wzoru jest taki sam jak podano wyżej.
l0 = β*lcol
Wartość współczynnika β należy przyjmować z tablicy lub wyliczać ze wzorów podanych w załączniku C normy.
Odległość między punktami podparcia słupa lcol jest podana na rysunku także w załączniku C.
Wpływ smukłości i obciążeń długotrwałych
na nośność słupów
W obliczeniach słupów określanych jako smukłe konieczne jest uwzględnianie wpływu obciążeń długotrwałych.
Z upływem czasu może nastąpić przyrost odkształceń (ugięć) słupa, który spowoduje przyrost mimośrodu działania siły długotrwałej.
W konsekwencji może nastąpić zniszczenie spowodowane wyboczeniem.
Słupy smukłe są bardziej podatne na wyboczenie niż krępe.
Podatność słupa ściskanego na wyboczenie ocenia się według wskaźnika λ wyrażającego smukłość elementu
![]()
λ = l0 / h lub λ = l0 / i
gdzie: h - wysokość przekroju prostokątnego,
i - promień bezwładności przekroju dowolnego.
Wpływ obciążeń długotrwałych uwzględnia się w obliczeniach nośności elementów smukłych jeżeli zachodzą warunki
dla elementów żelbetowych i sprężonych
l0 / h > 7 lub l0 / i >25
dla elementów betonowych l0 / h > 6 lub l0 / i >20
Wymiary słupa należy tak dobrać aby nie smukłość nie była większa niż
l0 / h ≤ 30 lub l0 / i ≤ 104
W żelbetowych elementach ściskanych, które uznaje się za smukłe (l0 / h > 7) uwzględniamy wpływ smukłości.
Zwiększamy mimośród początkowy e0 = ee + ea zgodnie z warunkiem
etot = η e0
gdzie: etot - mimośród całkowity,
η - współczynnik obliczany ze wzoru Timoszenki
na strzałkę ugięcia pręta zginanego
obciążonego siłą podłużną N
gdzie: NSd - obliczeniowa siła podłużna,
Ncrit - siła krytyczna.
Siła krytyczna Ncrit
Klasyczny wzór Eulera na siłę krytyczną
jest dla elementów żelbetowych zbyt dużym uproszczeniem.
Siła krytyczna musi być obliczana z uwzględnieniem stopnia zbrojenia i wpływu obciążeń długotrwałych.
Norma podaje następujący wzór na siłę krytyczną :
gdzie: Ecm, Es - moduły sprężystości betonu i stali,
Jc, Js - momenty bezwładności pól przekroju
betonu i zbrojenia,
klt - parametr uwzględniający wpływ działania
obciążenia długotrwałego,
W obliczeniach praktycznych siłę krytyczną liczymy metodą kolejnych przybliżeń.
Na wstępie obliczeń nie znamy przekroju zbrojenia , nie możemy więc określić wielkości Js.
Zakładamy szacunkowo przewidywany stopień zbrojenia słupa.
Jeżeli po zwymiarowaniu okażę się, że stopień zbrojenia elementu rożni się od założonego o więcej niż 10% to obliczenia należy powtórzyć.
PODSUMOWANIE
OBLICZANIE ZBROJENIA ŻELBETOWYCH SŁUPÓW PROSTOKĄTNYCH - MIMOŚRODOWO ŚCISKANYCH
1.Przyjęcie klasy betonu i stali.
2. Przyjęcie wymiarów przekroju słupa b oraz h
3. Obliczenie mimośrodu statycznego
ee = MSd / NSd
4.Obliczenie mimośrodu niezamierzonego
ea → z warunków normowych
5. Obliczenie mimośrodu początkowego
e0 = ea + ee
6.Obliczenie długości wyboczeniowej
l0 = β lcol
7. Obliczenie smukłości
l0 / h
8.Uwzględnienie wpływu obciążeń długotrwałych
etot = η e0
jeżeli l0 / h ≤ 7 to η = 1,0
jeżeli l0 / h > 7 to η =
9. Obliczenie przekroju zbrojenia słupa As1 oraz As2
według podanego niżej algorytmu.
Minimalne pole przekroju zbrojenia podłużnego
w elementach ściskanych
Minimalne pole przekroje całkowitego zbrojenia podłużnego należy określać z warunku normowego
As min ≥ 0,003Ac
As min ≥ 0,15
Maksymalne pole przekroju zbrojenia podłużnego
w elementach ściskanych
Całkowity przekrój zbrojenia podłużnego w słupach nieuzwojonych nie powinien być większy niż 4% pola przekroju użytecznego elementu
As max = 0,04 Ac
W słupach uzwojonych As max = 0,04 Ac
ODKSZTAŁCENIA I NAPRĘŻENIA PRZY ŚCISKANU
Mechanizm zniszczenia elementu ściskanego w stanie granicznym nośności zależy głównie od wielkości mimośrodu.
Na podstawie odkształceń granicznych betonu i zbrojenia w obliczeniach konstrukcji ściskanych wyróżnia się dwa przypadki:
przypadek dużego mimośrodu, kiedy
xeff / d ≤ ξeff,lim
przypadek małego mimośrodu, kiedy
xeff / d > ξeff,lim
W przypadku dużego mimośrodu charakter pracy i mechanizm zniszczenia jest podobny jak w belce zginanej.
Strefa rozciągana jest zwykle dość duża i tam rozpoczyna się proces niszczenia.
Stal zbrojenia rozciąganego osiąga granicę plastyczności, następuje zniszczenie przekroju.
W przypadku małego mimośrodu charakter pracy i zniszczenia jest podobny jak elementu osiowo ściskanego.
Strefa ściskana jest zwykle dość duża - w skrajnym przypadku cały przekrój może być ściskany.
Zniszczenie przekroju następuje wskutek wyczerpania nośności betonu w strefie ściskanej.
PRZYPADEK DUŻEGO MIMOŚRODU
ZBROJENIE NIESYMETRYCZNE
Wymiarowanie żelbetowego elementu prostokątnego polega na określeniu pola przekroju zbrojenia rozciąganego As1 oraz ściskanego As2 .
Obliczenia rozpoczynamy zawsze od przyjęcia założenia, że mamy do czynienia z przypadkiem dużego mimośrodu.
Korzystamy z ogólnych warunków równowagi momentów oraz sił - analogicznie jak w przypadku elementów zginanych.
Równanie równowagi sumy momentów zewnętrznych i wewnętrznych względem osi zbrojenia As1
NSd es1 = fcd b xeff (d - 0,5 xeff ) + fyd As2 (d - a2)
Równanie równowagi sumy rzutów zewnętrznej siły podłużnej oraz wypadkowych sił wewnętrznych na oś podłużną elementu
NSd = fcd b xeff + fyd As2 - fyd As1
Mamy trzy niewiadome As1, As2 oraz xeff -do dyspozycji natomiast dwa równania równowagi.
Aby wyeliminować jedną niewiadomą zakładamy pełne wykorzystanie strefy ściskanej przyjmując:
xeff = xeff, lim = ξeff, lim d
Podstawiamy tak zdefiniowane xeff do powyższych równań i po przekształceniach otrzymujemy praktyczne wzory do obliczania przekrojów zbrojenia As1 oraz As2.
Jeżeli założenie, że przekrój jest ściskany z dużym mimośrodem okaże się prawdziwe to na tym kończy się wymiarowanie.
Często jednak trudno jest jednoznacznie określić przypadek mimośrodu.
Podczas obliczeń mogą wystąpić pewne przypadki szczególne.
Przypadki szczególne
Jeżeli obliczone zbrojenie ściskane As2 będzie
As2 < 0 lub As2 < As min
to znaczy, że przyjęto zbyt duży przekrój betonowy słupa .
Zbrojenie ściskane jest niepotrzebne bo obciążenia przenosi sam beton.
Gdy ze względów konstrukcyjnych nie można zmniejszyć wymiarów słupa należy przyjąć:
As2 = As min
Następnie zbrojenie rozciągane As1 obliczyć przy założeniu
As2 = 0 ze wzorów podanych w algorytmie.
Jeżeli zbrojenie ściskane As2 >As min , natomiast
obliczone zbrojenie rozciągane As2 < 0 to znaczy, że zbrojenie to nie jest potrzebne. Mamy więc przypadek małego mimośrodu
PRZYPADEK MAŁEGO MIMOŚRODU
W projektowaniu można wtedy założyć, że siła
podłużna Nsd znajduje się w rdzeniu przekroju lub jego
pobliżu.
Na tej podstawie przyjęto:
ξeff = 1 (xeff / d = 1 czyli xeff =d)
κs = -1,0 (zbrojenie od strony mniej ściskanej jest
również ściskane)
Przekroje zbrojenia As1 oraz As2 obliczamy z warunków równowagi. Po przekształceniach otrzymamy praktyczne wzory do wymiarowania.
Przypadki szczególne
Jeżeli obliczone zbrojenie ściskane As2 jest ujemne lub mniejsze od minimalnego
As2 < 0 lub As2 < As min
należy zmniejszyć wymiary przekroju betonowego lub przyjąć As2 = As min. .
UWAGA !
W przypadku małego mimośrodu na rysunku układu sił w przekroju, przy zbrojeniu rozciąganym As1 pojawia się współczynnik κs.
Zbrojenie to może być rozciągane lub niekiedy ściskane.
Współczynnik κs obliczany ze wzoru podanego w normie przyjmuje wartości od - 1,0 do + 1,0.
Przy dużym mimośrodzie κs = 1,0 ( dlatego nie ma go na rysunku układu sił).
Przy małym mimośrodzie , jeżeli zbrojenie As1 jest ściskane wtedy κs = - 1,0 i wypadkowa w tym zbrojeniu zmienia znak.
PRZYPADEK MAŁEGO MIMOŚRODU
Jeżeli w obliczeniach pole przekroju zbrojenia rozciąganego As1 jest mniejsze od zera, to występuje przypadek małego mimośrodu. Zbrojenie As1 nie jest w pełni wykorzystane.
Pole przekroju zbrojenia rozciąganego należy przyjąć
As1 = As,min.
Dla wyznaczenia zbrojenia ściskanego As2 konieczna jest korekta założonego zasięgu strefy ściskanej i obliczenie rzeczywistego położenia osi obojętnej.
Z warunku równowagi momentów względem osi zbrojenia ściskanego, przyjmując As1 = 0, wyznacza się skorygowane położenie osi obojętnej xeff ze wzoru
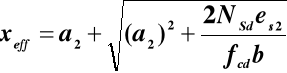
Jeżeli obliczone xeff ≤ d to pole przekroju zbrojenia As2 oblicza się ze wzoru, do którego podstawiamy obliczone wyżej xeff.
Przypadki szczególne
Jeżeli obliczone xeff ≥ d ,to oznacza, że cały przekrój jest ściskany. W tym przypadku zarówno zbrojenie As2 jak i zbrojenie As1 są ściskane.
Do dalszych obliczeń przyjmuje się:
xeff = d oraz κs = - 1,0
Pola przekroju zbrojenia As2 i As1 oblicza się ze skorygowanych wzorów podanych w algorytmie
Jeżeli przy założeniu xeff = d obliczone pola przekrojów zbrojenia As2 i As1 będą miały wartości ujemne lub mniejsze od minimalnych, to należy przyjąć minimalne zbrojenie konstrukcyjne As1 = As2 = As,min.
Oznacza to, że przyjęto zbyt duże wymiary przekroju betonowego.
ZBROJENIE SYMETRYCZNE
As1 = As2
W wielu przypadkach z warunków pracy elementu wynika potrzeba użycia zbrojenia symetrycznego, np. gdy na element działają momenty o różnych znakach ale zbliżone co do bezwzględnej wartości.
Zbrojenie symetryczne jest chętnie stosowane w wykonawstwie ze względu na prostotę montażu.
OBLICZANIE ZBROJENIA
Przy założeniu As1 = As2, z warunku równowagi sił
NSd = fcd b xeff + fyd As2 - fyd As1
otrzymamy wielkość strefy ściskanej
xeff =
Jeżeli xeff ≤ xeff, lim = ξeff, lim d - to mamy przypadek dużego mimośrodu
Zbrojenie liczymy ze wzoru
Jeżeli xeff > xeff, lim = ξeff, lim d - to mamy przypadek małego mimośrodu
Zbrojenie liczymy ze wzoru
SŁUPY UZWOJONE O PRZEKROJU KOŁOWYM
W słupach o przekroju kołowym zamiast strzemion stosuje się uzwojenie spiralne. Ten rodzaj zbrojenia ogranicza swobodę odkształceń poprzecznych betonu i zwiększa wytrzymałość słupa na ściskanie.
Poprzednie normy ograniczały stosowanie słupów uzwojonych do przypadku osiowego ściskania. Obecna norma znosi to ograniczenie i pozwala w obliczeniach nośności uwzględniać wpływ mimośrodu siły, klasy betonu, stopnia zbrojenia podłużnego, smukłości słupa i czasu trwania obciążenia .
Wpływ uzwojenia na nośność słupów może być uwzględniany jedynie, gdy są spełnione następujące warunki:
całkowity mimośrod siły etot ≤ 0,125 dcore,
skok linii śrubowej uzwojenia sn ≤ 0,2 dcore oraz
sn ≤ 80 mm.
Nośność słupa uzwojonego można obliczać tak jak zwykłych słupów żelbetowych o średnicy dcore, zastępując jednoosiową wytrzymałość betonu fcd wytrzymałością betonu rdzenia fcore,cd wyznaczoną ze wzoru:
|
|
w którym:
|
|
|
|
|
|
przy czym: Ast - pole przekroju uzwojenia,
![]()
- obliczeniowa granica plastyczności stali
uzwojenia.
Gdy smukłość słupa l0/i = 4l0/dc ≤ 25, mimośród należy przyjmować równy mimośrodowi początkowemu e0 wyliczonemu bez uwzględniania wpływu smukłości i obciążeń długotrwałych.
Przy smukłości słupa l0/i > 25 mimośród całkowity etot należy wyznaczać z uwzględnieniem wpływu smukłości i obciążeń długotrwałych.
STANY GRANICZNE UŻYTKOWALNOŚCI
Stany graniczne użytkowalności obejmują sytuacje, w których konstrukcja staje się nieprzydatna do normalnej eksploatacji.
Do stanów granicznych użytkowalności należą:
stan graniczny ugięć,
stan graniczny zarysowania,
stan graniczny naprężeń (tylko dla konstrukcji sprężonych).
Sprawdzenie stanów granicznych użytkowalności polega na wykazaniu, że spełniony jest warunek
Ed ≤Cd
gdzie: Ed - obliczeniowy efekt oddziaływań
(np. szerokość rysy lub ugięcie),
Cd - graniczna wartość efektu
ustalona przez normę.
Licząc ugięcie lub zarysowanie przyjmujemy:
długotrwałych obciążeń charakterystycznych (γf = 1,0),
sprężystości betonu (Ecm)
|
STAN GRANICZNY ZARYSOWANIA
Występowanie rys w konstrukcjach żelbetowych jest nieuniknione, wynika bowiem ze skomplikowanej struktury betonu.
Podstawową przyczyną zarysowania konstrukcji jest osiągnięcie przez beton wytrzymałości na rozciąganie w najbardziej wytężonych przekrojach.
W elementach zginanych powstają rysy prostopadłe - w miejscach działania maksymalnych momentów.
Rysy ukośne lokalizują się w obszarach działania dużych sił poprzecznych.
Rysy skurczowe mogą powstać jeszcze przed obciążeniem konstrukcji, w pierwszych dniach po uformowaniu betonu.
Właściwa pielęgnacja skutecznie ogranicza występowanie mikrorys, których jednak nie można całkowicie wyeliminować.
Wybrane rodzaje zarysowań
Sprawdzanie stanu granicznego zarysowania
Zarysowanie elementów należy kontrolować już na etapie projektowania tak dobierając przekrój betonu i stali, aby nie wystąpiły rysy o nadmiernej szerokości rozwarcia.
Rysy takie są niedopuszczalne ze względu na trwałość i estetykę.
Wymagane jest spełnienie warunku
wk ≤ wlim
gdzie: wk - szerokość rysy obliczona dla
kombinacji długotrwałych obciążeń
charakterystycznych,
wlim - graniczna (ustalona w normie) szerokość
rysy prostopadłej lub ukośnej.
Graniczne szerokości rys wlim podane są w normie w tablicy 7
Tablica 7 - Graniczne szerokości rys wlim
w konstrukcjach żelbetowych
Graniczne wartości szerokości rys przyjmuje się także
odpowiednio do wymagań inwestora
Informacje o klasach ekspozycji w zależności od warunków środowiska podane są w normie w tablicy 5
Dla najczęściej występujących klas ekspozycji graniczna szerokość rysy wynosi
wlim = 0,3 mm
Doświadczalny pomiar szerokości rysy powinien być wykonany na poziomie rozciąganych prętów zbrojenia podłużnego ( w odległości równej grubości otuliny).
Szerokość rysy na krawędzi elementu jest niemiarodajna, gdyż często z powodu wykruszania się betonu jest zbyt duża.
Uproszczony sposób sprawdzania
stanu granicznego zarysowania
Obliczanie szerokości rozwarcia rys jest stosunkowo pracochłonne.
W wielu przypadkach nie ma potrzeby wykonywania szczegółowych obliczeń.
Uproszczone sprawdzenie można wykonać posługując się tablicą D1 (podaną w załączniku D normy).
Należy porównać przyjętą w projekcie średnicę
zbrojenia φ z wartością φmax odczytaną z tabeli.
Sprawdzenie warunku
φ ≤ φmax |
oznacza, że szerokość rys w projektowanym elemencie nie przekroczy 0,3mm.
Obliczenie szerokości rozwarcia rys prostopadłych należy przeprowadzać jedynie wtedy, gdy użyto zbrojenia o tak dużej średnicy, że φ >φmax .
φ > φmax φ ≤ φmax
Szerokości rys prostopadłych w elementach zginanych o przekroju prostokątnym zbrojonych stalą żebrowaną
(klasy A-II, A-III, A-IIIN) można uznać za nie większą
niż wlim = 0,3 mm jeżeli maksymalna średnica prętów podłużnych zbrojenia rozciąganego nie przekracza φmax z tablicy D1.
Określenie momentu rysującego
W stanach granicznych użytkowalności rozróżnia się dwie podstawowe sytuacje, w których przekrój jest:
zarysowany
niezarysowany.
W elementach zginanych kryterium różnicującym jest moment rysujący Mcr .
Wielkość momentu rysującego zależy od wymiarów przekroju poprzecznego oraz średniej wytrzymałości betonu na rozciąganie fctm .
Dla elementu o przekroju prostokątnym (b h)
Mcr = fctm .Wc
gdzie: Wc - wskaźnik wytrzymałości przekroju
Wc = b h2 / 6
STANY GRANICZNE UŻYTKOWALNOŚCI
Założenia ogólne do obliczeń metodą dokładną
Zgodnie z normą sprawdzanie stanów granicznych użytkowalności należy prowadzić wg zasad analizy liniowo sprężystej.
Momenty statyczne i bezwładności, wskaźniki wytrzymałości, położenie osi obojętnej, a także naprężenia w betonie i zbrojeniu oblicza się zakładając, że:
obowiazuje zasada płaskich przekrojów,
stal jest materiałem sprężystym o module Es,
beton jest materiałem sprężystym przy ściskaniu i
rozciąganiu do momentu zarysowania (faza I),
po zarysowaniu beton nie przenosi naprężeń
rozciągających, a przy ściskaniu pracuje jak materiał
sprężysty (faza II).
Elementy zginane
W obliczeniach elementów zginanych wyróżnia się
I i II fazę.
W fazie I czyli tuż przed pojawieniem się rysy uwzględnia się wytrzymałość betonu na ściskanie i rozciąganie.
W fazie II, po zarysowaniu beton strefy zarysowanej ma zerową wytrzymałość, w strefie ściskanej pracuje jak materiał sprężysty.
Zakładamy, że beton i stal są powiązane siłami przyczepności więc ich odkształcenia pod obciążeniem są jednakowe.
Wspólną odkształcalnośćobu materiałów przy obciążeniach krótkotrwałych określa współczynnik:
Przy obciążeniach długotrwałych konieczne jest uwzględnienie wpłwu pełzania i wtedy współczynnik ten ma postać:
Zgodnie z założoną teorią liniowej sprężystości żelbetu należy przyjąć tzw. sprowadzone pole przekroju zbrojenia czyli zamienić przekrój stalowy na zastępczy betonowy.
Pozwala to traktować żelbet jak materiał jednorodny.
Przy tym założeniu położenie osi obojętnej oblicza się z równania sumy momentów statycznych pól powierzchni strefy ściskanej Acc i sprowadzonego przekroju zbrojenia rozciąganego αe,tAs1 z zależności
Pierwiastek rzeczywisty powyższego równania, a więc wysokość strey ściskanej w fazie II, określa wzór
Szerokość rys prostopadłych - metoda dokładna
Szerokość rysy w poziomie zbrojenia rozciąganego zależy przede wszystkim od wielkości odkształceń związanych
z wydłużeniem się zbrojenia na odcinku między rysami. Odkształcenia betonu rozciąganego są pomijalnie małe .
Obliczeniowa szerokość rys prostopadłych do osi elementu
wk = β srm εsm |
|
β - współczynnik wyrażający stosunek obliczeniowej
szerokości rysy do szerokości średniej,
srm - średni końcowy rozstaw rys,
εsm - średnie odkształcenie zbrojenia rozciąganego.
Wartość β uzależnia się od rodzaju działających obciążeń oraz od wymiarów zewnętrznych przekroju:
β = 1,7 niezależnie od wymiarów przekroju w przypadku zarysowania spowodowanego obciążeniem bezpośrednim i zarysowania wywołanego odkształceniem wymuszonym (np. skurczem betonu), gdy najmniejszy wymiar nie przekracza 800 mm,
β = 1,3 w przypadku zarysowania spowodowanego oporem stawianym odkształceniom wymuszonym w przekrojach, którego najmniejszy wymiar nie przekracza 300 mm.
Dla przekrojów o wymiarach pośrednich wartości β można interpolować liniowo.
Średni, końcowy rozstaw rys srm oblicza się z empirycznego wzoru, w którym uwzględnia się wpływ tak istotnych czynników, jak średnica i rodzaj pręta oraz stopień zbrojenia:
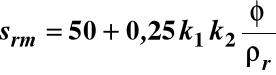
φ - średnica pręta w [mm]; gdy stosuje się pręty o różnej średnicy przyjmuje się wartość średnią;
k1 -współczynnik zależny od przyczepności prętów;
k1 = 0,8 dla prętów żebrowanych,
k1 = 1,6 dla prętów gładkich;
k2 - współczynnik zależny od rozkładu naprężeń
rozciągających,
k2 = 0,5 przy zginaniu;
k2 = 1,0 przy rozciąganiu osiowym,
k2 = (ε1 + ε2)/(2ε1) przy rozciąganiu mimośrodowym,
gdzie ε1 i ε2 to maksymalne i minimalne odkształcenie na krawędziach przekroju zarysowanego przy założeniu liniowego rozkładu odkształceń;
ρr -efektywny stopień zbrojenia As / Act,eff:,
gdzie As jest polem przekroju zbrojenia zawartego wewnątrz efektywnego pola Act,eff przekroju strefy ściskanej.
Zasady określanie pola Act,eff dla belek, płyt i elementów rozciąganych (rys 33)
(xII - wysokość strefy ściskanej przekroju zarysowanego)
Średnie odkształcenie zbrojenia rozciąganego εsm, którego wartość zależy od stopnia wytężenia zbrojenia i warunków przyczepności:
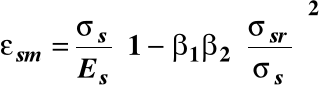
σs - naprężenie w zbrojeniu rozciąganym,
σsr - naprężenie w zbrojeniu rozciąganym, obliczone dla
obciążenia powodującego zarysowanie,
β1 - współczynnik zależny od przyczepności prętów:
β1 = 1,0 dla prętów żebrowanych,
β1 = 0,5 dla prętów gładkich,
β2 -współczynnik zależny od czasu działania i
powtarzalności obciążenia:
β2 = 1,0 dla jednokrotnego obciążenia krótkotrwałego,
β2 = 0,5 dla obciążeń długotrwałych lub wielokrotnie
powtarzalnych.
Ponieważ naprężenia w elemencie są proporcjonalne do sił, które je spowodowały, norma pozwala przyjmować zamiast stosunku σsr / σs:
przy zginaniu Mcr / MSd ,
przy rozciąganiu Ncr / NSd .
W odniesieniu do elementów poddanych działaniu tylko wewnętrznych odkształceń wymuszonych (np. skurcz betonu) można przyjmować σs = σsr.
Szerokość rys ukośnych
Zgodnie z normą można odstąpić od sprawdzania szerokości rys ukośnych w pewnych, ściśle określonych przypadkach.
Warunki, jakie musi spełniać element, w którym nie trzeba wyznaczać szerokości rys ukośnych, są następujące:
zbrojenie na ścinanie ma postać tylko strzemion pionowych,
strzemiona pionowe są wykonane ze stali A-0 o średnicy φ1 ≤ 8 mm,
w obliczeniach nośności na ścinanie przyjęto
cot θ ≤ 1,75,
element mieści się w klasie ekspozycji środowiska dla
których wlim = 0,3 mm.
W innych przypadkach sprawdzanie szerokości rys jest konieczne.
Szerokość ta może być obliczana ze wzoru:
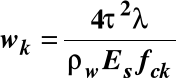
τ - naprężenie ścinające w przekroju elementu
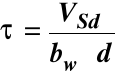
ρw = ρw1 + ρw2 - stopień zbrojenia na ścinanie strzemionami
i prętami odgiętymi
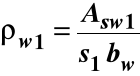
, 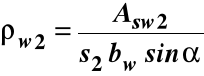
λ - współczynnik obliczany ze wzoru
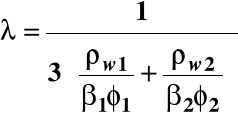
φ1, φ2 - odpowiednio: średnica strzemion i prętów
odgiętych,
β1, β2 - współczynniki zależne od;
przyczepności strzemion (β1),
prętów odgiętych (β2)
1,0 - dla prętów gładkich,
0,7 - dla prętów żebrowanych.
Obliczanie wartości ugięć metodą dokładną
Strzałkę ugięcia zginanego elementu żelbetowego można obliczać, stosując ogólny wzór z mechaniki budowli
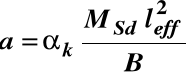
αk - współczynnik zależny od schematu statycznego
i sposobu obciążenia belki, wyznaczany według zasad
mechaniki budowli,
MSd - maksymalny moment zginający od obciążeń
długotrwałych (γf = 0),
B - sztywność przekroju, w którym występuje moment
obliczeniowyMSd.
W belce idealnie sprężystej z materiału jednorodnego sztywność B = EI jest wartością stałą.
W belce żelbetowej sztywność zależy nie tylko od właściwości materiałowych (E) i wymiarów przekroju (I), ale istotne znaczenie ma zarysowanie i czas działania obciążenia. |
Dokładne uwzględnienie wpływu zarysowania i pełzania betonu na wzrost krzywizny elementu jest trudne do określenia i w praktycznych obliczeniach przyjmuje się szereg uproszczeń. Podstawowym założeniem jest przyjęcie dwóch faz wytężenia przekrojów żelbetowych; niezarysowanej i zarysowanej.
Obliczanie ugięć elementów żelbetowych należy więc rozpocząć od ustalenia (analogicznie jak w stanie granicznym zarysowania), czy element pracuje jako:
niezarysowany w fazie I (Mcr > MSd),
zarysowany w fazie II (Mcr < MSd).
W przypadku elementu niezarysowanego przyjmuje się stałą sztywność B = EI na całej długości elementu.
Niewielkie odkształcenia, spowodowane małym momentem MSd, mają charakter sprężysty i cały przekrój bierze udział w przenoszeniu obciążeń. Można więc przyjąć stałą sztywność na długości niezarysowanej belki.
Sztywność elementów niezarysowanych w ujęciu normy zależy także od czasu działania obciążenia:
dla obciążeń długotrwałych
B∞ = Ec,eff II
dla obciążeń krótkotrwałych
B0 = Ecm II
Ec,eff - efektywny moduł sprężystości (z uwzględnieniem
pełzania betonu),
Ecm - średni moduł sprężystości betonu,
II - sprowadzony moment bezwładności w fazie I.
Zarysowanie powoduje znaczne zmniejszenie sztywności elementu, to pociąga za sobą wzrost ugięcia.
W przekroju zarysowanym beton nie przenosi naprężeń rozciągających, choć nadal współpracuje ze stalą na odcinkach między rysami. Maleje wartość modułu sprężystości betonu, sztywność zmienia się na długości elementu.
Sztywność belki żelbetowej: a) niezarysowanej b) zarysowanej
Sztywność B∞ elementów zarysowanych długotrwale obciążonych
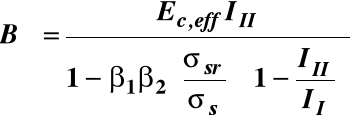
β1, β2, σs, σsr - zmienne określone we wzorze na średnie
odkształcenie zbrojenia zarysowanego,
III - sprowadzony moment bezwładności w fazie II,
σsr / σs - można zastąpić stosunkiem Mcr / MSd.
Efektywny moduł sprężystości oblicza się w zależności od czasu t działania obciążenia:
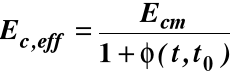
Zmiana wartości modułu sprężystości wraz z upływem czasu wynika z wpływu pełzania na końcowe ugięcie elementów długotrwale obciążonych.
Końcową wartość współczynnika pełzania φ∞,to przyjąć z tablicy A1
.
Sztywność B0 elementów zarysowanych krótkotrwale obciążonych
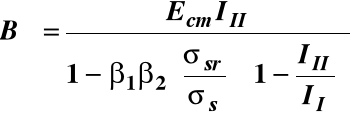
w którym uwzględniono średni moduł sprężystości betonu.
Wartości zmiennych β2, σs, II, III muszą być określane przy obciążeniu krótkotrwałym.
Odrębnym zagadnieniem spotykanym w praktyce jest ocena ugięć wywołanych dodatkowym obciążeniem.
W czasie eksploatacji konstrukcji długotrwale obciążonej może wystąpić konieczność krótkotrwałego przyłożenia dodatkowego obciążenia. W takiej sytuacji nastąpi przyrost istniejącego już ugięcia.
Na rysunkach przedstawiono działanie obciążenia krótkotrwałego na element, który ugiął się wcześniej pod wpływem obciążeń długotrwałych.
Rysunek a) pokazuje wykres ugięcia początkowego a 0,d
i końcowego a ∞,d , gdy na belkę działa tylko obciążenie długotrwałe (d).
Krótkotrwałe przyłożenie obciążenia całkowitego opisuje wykres początkowego ugięcia a 0,k+d (rys. b). Można zauważyć, że wykres ten uwzględnia już ugięcie na skutek obciążenia długotrwałego.
Przyrost ugięcia spowodowanego dodatkowym obciążeniem krótkotrwałym (k) wyraża więc różnica
[a 0,k+d - a 0,d].
Ostateczne ugięcia pod łącznym działaniem obciążenia krótko i długotrwałego (rys. c) określa zależność:
a = a ∞,d + [a 0,k+d - a 0,d]
a ∞,d- ugięcie długotrwałe, wywołane obciążeniem długotrwałym (do wzoru na wartość ugięcia podstawia się moment od obciążeń długotrwałych i sztywność B∞),
a 0,k+d - ugięcie, które powstałoby natychmiast po jednoczesnym przyłożeniu obciążeń krótko i długotrwałych (do wzoru na wartość ugięcia podstawia się moment pochodzący od obciążeń całkowitych i sztywność B0),
a 0,d - ugięcie, które powstałoby natychmiast po przyłożeniu obciążeń długotrwałych (do wzoru na wartość ugięcia podstawia się moment pochodzący od obciążeń długotrwałych i sztywność B0).
Opisany efekt działania obciążenia krótkotrwałego na element, który wcześniej ugiął się pod działaniem obciążenia długotrwałego, przedstawiono zgodnie z normą przyjmując zasadę superpozycji składowych ugięć.
W normie nie podano jednak wartości granicznych, z którymi można by porównać otrzymany wynik, gdyż ugięcia graniczne podane w tablicy 13 dotyczą jedynie elementów długotrwale obciążonych. Zaleca się więc przyjmować ograniczenie ugięć w zależności od indywidualnych wymagań w rozpatrywanym przypadku.
STAN GRANICZNY UGIĘĆ
Ugięcie (przemieszczenie) konstrukcji jest odpowiedzią na przyłożone obciążenie.
Na wielkość ugięcia ma wpływ wiele czynników, które trudno jest w ścisły sposób uwzględnić w obliczeniach.
Szczególne znaczenie mają zjawiska związane z upływem czasu jak, pełzanie betonu.
Dlatego w normach zaleca się obliczanie ugięć elementów wywołanych kombinacją obciążeń długotrwałych.
Działające długotrwale obciążenie może wywołać nadmierne ugięcie, które pogorszy estetykę wnętrza, poczucie bezpieczeństwa użytkowników lub warunki użytkowania.
Sprawdzenie stanu granicznego ugięć
Weryfikacja stanu granicznego ugięć polega na wykazaniu, że ugięcie elementu ak nie przekroczą wartości określanych jako graniczne.
Wymagane jest spełnienie warunku
ak ≤ alim
gdzie: ak - ugięcie obliczone dla
kombinacji długotrwałych obciążeń
charakterystycznych,
alim - graniczna (ustalona w normie) wartość
ugięcia.
Według normy kontrola ugięć jest konieczna w elementach dachowych i stropowych w budownictwie ogólnym, przemysłowym i rolniczym( jeżeli warunki użytkowania nie wymagają specjalnego ograniczenia ugięć).
Graniczną wartość ugięć podaje w normie tablica 8.
Uproszczony sposób sprawdzania
stanu granicznego zarysowania
Uproszczony sposób weryfikacji stanu granicznego ugięć polega na kontroli wskaźnika sztywności elementu.
Wskaźnik ten określany jest jako stosunek długości obliczeniowej elementu leff do wysokości użytecznej przekroju d.
Projektując element należy tak dobrać wymiary, a co za tym idzie wskaźnik leff / d ,aby nie przekroczyć wartości granicznej (leff / d)lim podanej w tablicy 15 w normie.
Wartość (leff / d)lim określa się w zależności od:
rodzaju konstrukcji,
schematu statycznego,
stopnia zbrojenia,
klasy betonu,
wartości naprężeń w zbrojeniu rozciąganym.
Tablica 13 Maksymalne wartości stosunku rozpiętości leff
do wysokości użytecznej d, przy której można nie
sprawdzać ugięć
W ogólnej formie normowy warunek kontroli ugięć
ma postać:
gdzie: δ1 - współczynnik korekcyjny w przypadku gdy
rozpiętość elementu leff > 6 m
δ1 = w przypadku stropów i
stropodachów
δ1 = w przypadku przekryć
dachowych
δ2 - współczynnik korekcyjny w przypadku gdy
w zbrojeniu występuje inny poziom naprężeń σs
δ2 = 250 / σs
Uwaga:
Projektując element o dużej rozpiętości leff > 7,5 m należy zawsze przyjmować jego wysokość z warunku nie przekroczenia ugięć granicznych.
ZASADY KSZTAŁTOWANIA I PROJEKTOWANIA
ELEMENTÓW ŻELBETOWYCH
PŁYTY
Charakter pracy statycznej płyt zależy od proporcji wymiaru szerokości płyty lx do jej długości ly.
Wyróżnia się dwa podstawowe rodzaje:
płyty jednokierunkowo zbrojone,
płyty dwukierunkowo zbrojone.
Płyty jednokierunkowo zbrojone
Płyty jednokierunkowo zbrojone mają kształt wydłużonego prostokąta, gdzie:
ly / lx > 2,0
Stosowane są powszechnie w monolitycznych stropach płytowo-żebrowych.
Zginanie płyty rozpatruje się tylko w kierunku krótszego boku. W kierunku dłuższego boku ugięcie płyty jest pomijalnie małe.
W obliczeniach płyta traktowana jest jak belka ciągła o umownej szerokości jednego metra.
W miejscach żeber, z którymi płyta jest sztywno połączona
mamy podpory pośrednie belki ciągłej.
PŁYTY KRZYŻOWO ZBROJONE
Płyty dwukierunkowo zbrojone mają kształt zbliżony do kwadratu, gdzie:
0,5 ≤ ly / lx ≤ 2,0
Stosowane są jako stropy płytowo-żebrowe, kasetonowe lub rusztowe w budownictwie ogólnym.
Pracują jako ściany w obiektach przemysłowych i konstrukcjach inżynierskich (zbiorniki, zasobniki, ściany oporowe, itp.)
Najczęściej mają kształt kwadratu, prostokąta, lecz także trapezu, trójkąta, koła.
W obliczeniach przyjmowane są jako rzeczywiste ustroje płytowe zginane w dwu płaszczyznach.
Przyjmowanie grubości płyty
Grubość płyty zależy przede wszystkim od rozpiętości oraz obciążenia.
Minimalną grubość płyt określa się z warunków normowych, w których główne aspekty to:
przeznaczenie,
nie przekroczenie granicznych wartości ugięć.
Minimalne grubości płyt ze względu na przeznaczenie podano w tablicy 28.
Grubość płyty należy tak dobrać do jej rozpiętości, aby płyta miała odpowiednią sztywność. Pozwala to uniknąć nadmiernych ugięć.
Stosunek rozpiętości płyty leff do wysokości użytecznej przekroju d należy przyjmować:
- w przypadku płyt wolno podpartych jednokierunkowo zbrojonych
- w przypadku płyt zamocowanych i ciągłych jednokierunkowo oraz krzyżowo zbrojonych.
W każdym przypadku grubość płyty nie może być mniejsza niż to wynika z:
warunku nie przekroczenia granicznych wartości ugięć alim (patrz tablica 10),
warunku prawidłowego otulenia,
przepisów przeciwpożarowych.
Przy określaniu grubości płyty należy mieć także na uwadze ekonomiczny stopień zbrojeni, który zaleca się przyjmować:
0,7% ≤ ρ ≤ 1,2%
Zbrojenie płyt
Pole przekroju zbrojenia głównego płyt oblicza się według zasad omówionych dla elementów zginanych.
Dodatkowo w kierunku prostopadłym do zbrojenia głównego umieszcza się pręty rozdzielcze.
Minimalne średnice oraz zasady rozmieszczania zbrojenia podają warunki normowe.
Pręty główne:
średnica prętów zbrojenia Φ ≥ 4,5 mm,
średnica drutów w siatkach zgrzewanych
Φ ≥ 3,0 mm,
do podpory należy doprowadzić bez odgięć nie mniej niż 1/3 dolnych prętów potrzebnych w przęśle i nie mniej niż 3 pręty na 1 m szerokości przekroju,
rozstaw prętów zbrojenia głównego nie powinien być większy niż:
przy zbrojeniu jednokierunkowym
250 mm i 1,2h dla h > 100 mm
120 mm dla h ≤ 100 mm
przy zbrojeniu dwukierunkowym - 250 mm.
Pręty rozdzielcze:
pręty rozdzielcze powinny mieć rozstaw nie większy niż 300 mm (3 na 1 m szerokości płyty).
Praca statyczna a zbrojenie płyt
Płyty jednokierunkowo zbrojone mogą być zbrojone prętami pojedynczymi lub siatkami zgrzewanymi.
Układ zbrojenia podłużnego zależy od schematu statycznego płyty i wynika z przebiegu momentów zginających.
Płyta wolno podparta
Schemat ten w praktyce występuje rzadko. Zazwyczaj nie ma swobody obrotu na podporze.
Płyta zamocowana częściowo na podporze
Częściowe lub całkowite zamocowanie na podporze powoduje pojawienie się ujemnych momentów podporowych.
Płyta wspornikowa
Zbrojenie główne rozmieszczone w górnej strefie rozciąganej powinno być starannie zakotwione.
BELKI
Belkami nazywamy prętowe elementy zginane.
Wykonywane są jako monolityczne lub prefabrykowane.
Belki żelbetowe stosowane są w stropach i stropodachach, układach ramowych płaskich i przestrzennych.
W ustrojach monolitycznych kształt przekroju poprzecznego belek jest przeważnie prostokątny lub teowy.
Kształt belek prefabrykowanych bywa bardziej zróżnicowany, dzięki specjalnym formom stosowanym w zakładach prefabrykacji.
Przekroje poprzeczne belek żelbetowych
Wymiary przekroju poprzecznego
W celu ujednolicenia wymiarów belek monolitycznych
norma zleca następujące stopniowanie wymiarów:
szerokość belek prostokątnych i żeber belek teowych przyjmuje się - 150, 180, 200 mm i dalej co 50 mm,
wysokość belek prostokątnych i teowych
przyjmuje się - 250, 300 mm i dalej co 50 mm do
800 mm ,a powyżej 800 mm stopniuje się co 100 mm .
W belkach monolitycznych proporcja wymiarów wynosi zazwyczaj
|
W przypadku gdy
h > 4b
element zalicza się do belek wysokich zwanych też belkami-ścianami, które należy projektować zgodnie z teorią układów tarczowych.
Podstawowy wpływ na wymiary przekroju belki mają wymagania stanów granicznych.
zginanie
STAN GRANICZNY NOŚNOŚCI
ścinanie
ugięcie
STANY GRANICZNE
UŻYTKOWALNOŚCI
zarysowanie
W typowych przypadkach najistotniejszy jest wpływ zginania oraz ugięć.
Przyjmując wymiary belki ze względu na :
zginanie - należy zakładać ekonomiczny stopień zbrojenia, w granicach
0,9% ≤ ρ ≤ 1,5%
stan graniczny ugięć - zaleca się określać wysokość użyteczną d z warunków
dla belek głównych dla belek drugorzędnych
W krótkich mocno obciążonych belkach decydujący będzie wpływ ścinania.
W sytuacjach gdy wymagana jest szczelność o wymiarach elementu może zadecydować stan zarysowania.
Zbrojenie belek
Zbrojenie belek stanowią pręty główne, montażowe oraz strzemiona.
Pręty główne:
średnica prętów rozciąganych Φ ≥ 8 mm,
średnica prętów ściskanych Φ ≥ 12 mm,
(belki monolityczne)
średnica prętów ściskanych Φ ≥ 10 mm,
(belki prefabrykowane)
do podpory należy doprowadzić bez odgięć co najmniej 1/3 dolnych prętów potrzebnych w przęśle oraz nie mniej niż 2 pręty,
jeżeli wysokość belki jest większa od 700 mm, to przy powierzchniach bocznych należy umieścić pręty konstrukcyjne o średnicy Φ ≥ 8 mm, w rozstawie nie większym niż 250 mm .
Strzemiona:
średnica strzemion Φ ≥ 4,5 mm
(belki monolityczne),
średnica strzemion Φ ≥ 3,0 mm
(belki prefabrykowane).
Ponadto średnica strzemion nie mniejsza niż 0,2 średnicy zbrojenia głównego.
Maksymalna średnica strzemion z prętów gładkich nie większa niż 12 mm .
Maksymalny odstęp strzemion smax
− w kierunku podłużnym
smax ≤ 0,75 d, smax ≤ 400 mm
− w kierunku poprzecznym
smax ≤ d, smax ≤ 400 mm
Stopień zbrojenia strzemionami na ścinanie nie może byś mniejszy niż:
− na odcinkach drugiego rodzaju
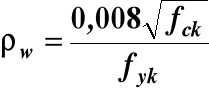
− na odcinkach pierwszego rodzaju określamy z
ogólnych warunków konstrukcyjnych
W belkach prostokątnych nie połączonych z płytami należy stosować strzemiona zamknięte.
W belkach o szerokości większej niż 35 cm, zbrojonych w strefie rozciąganej więcej niż 3 prętami ,należy stosować strzemiona czteroramienne.
SŁUPY
Słupy to elementy prętowe poddane działaniu sił podłużnych często w połączeniu z momentem zginającym.
Słupy przekazują obciążenia na niższą część układów konstrukcyjnych lun na fundament.
Wykonywane są jako monolityczne i prefabrykowane.
Wyróżnia się dwa podstawowe rodzaje:
słupy nieuzwojone, w których przekrój poprzeczny ma kształt kwadratu, prostokąta, wielokąta, itd.
słupy uzwojone, których przekrój poprzeczny ma kształt koła.
Słupy mają najczęściej stały przekrój poprzeczny na wysokości kondygnacji.
W budynkach wielokondygnacyjnych może być on zwiększany ze wzrostem obciążeń. W halach przemysłowych wyposażonych w suwnice przekrój słupa zmienia się odcinkowo.
Zróżnicowane kształty słupów nieuzwojonych
Wymiary przekroju poprzecznego
Wymiary przekroju poprzecznego słupów monolitycznych przyjmuje się następująco:
przy boku o długości do 60 cm - z zaokrągleniem
do 5 cm ,
przy boku długości powyżej 60 cm - z zaokrągleniem
do 10 cm .
Zaleca się ograniczenie smukłości słupów zgodnie z warunkami podanymi w normie
gdzie:
l0 - długość obliczeniowa słupa,
h - większy bok słupa prostokątnego,
i - promień bezwładności przekroju o kształcie
dowolnym.
Jeżeli słup nie jest kwadratowy proporcje między wymiarami przekroju poprzecznego wynoszą zazwyczaj
W przypadku działania na słup momentów zginających, większy bok słupa h jest zawsze równoległy do płaszczyzny
działania momentów.
Zbrojenie słupów
Pręty podłużne
Zbrojenie podłużne słupów monolitycznych wykonuje się z prętów o średnicy od 12 do 40 mm .
W słupach prefabrykowanych można stosować pręty o średnicy 10 mm .
W każdym narożu słupa powinien znajdować się jeden pręt w odstępie nie przekraczającym 40 cm .
W przekroju okrągłym minimalna liczba prętów
wynosi 6 sztuk.
Minimalna liczba prętów
Całkowity przekrój poprzeczny zbrojenia podłużnego słupów nie powinien być większy niż 4% powierzchni przekroju słupa.
Bez istotnej potrzeby nie należy przekraczać stopnia zbrojenia ρ = 3% .
Strzemiona
Zasadniczym zadaniem strzemion w słupie jest zabezpieczenie prętów podłużnych przed wyboczeniem.
Łączą one i stężają pręty główne przed oraz w czasie betonowania.
Im mniejsza średnica zbrojenia słupa tym gęściej rozmieszczamy strzemiona stabilizujące pręty podłużne.
Rozstaw strzemion nie powinien być większy niż:
15 Φ zbrojenia podłużnego, gdy stopień zbrojenia słupa ρ ≤ 3% ,
10 Φ zbrojenia podłużnego, gdy stopień zbrojenia słupa ρ > 3% ,
najmniejszy wymiar poprzeczny słupa lub jego średnicy i nie więcej jak 40 cm .
W miejscu łączenia prętów zbrojenia podłużnego, a także w miejscu zmiany przekroju poprzecznego słupa rozstaw ten powinien być zmniejszony do połowy.
Na końcach słupów prefabrykowanych rozstaw strzemion należy zagęścić do 1/3 rozstawu maksymalnego.
Strzemiona pojedyncze stosuje się tylko wtedy gdy:
wymiar boku słupa nie jest większy niż 45 cm ,
liczba prętów zbrojenia podłużnego z każdej strony nie większa niż4 ,
stopień zbrojenia słupa nie jest większy niż 3% .
Strzemiona w słupach a) pojedyncze
b), c) podwójne
Zbrojenie słupów uzwojonych
Słupy uzwojone można projektować tylko wtedy, gdy mimośród statyczny siły ściskającej ee = 0.
Wpływ uzwojenia może być uwzględniany w obliczeniach jeżeli smukłość słupa l0 / d ≤ 10 , a skok linii śrubowej uzwojenia spełnia warunki
sn ≤ 0,2 dcore sn ≤ 80 mm
Zbrojenie słupów uzwojonych
Zbrojenie podłużne powinno składać się z co najmniej
6 prętów o średnicy 12 do 32 mm .
Średnica prętów uzwojenia nie powinna być mniejsza niż 4,5 mm .
Uzwojenie należy przeprowadzić przez całą wysokość belki opierającej się na słupie.
Obliczanie i konstruowanie
płyt dwukierunkowo zbrojonych
Obliczenia płyt dwukierunkowo zbrojonych przeprowadza się dwoma metodami:
- wg teorii sprężystości
-wg teorii nośności granicznej.
Założenia do obliczeń:
grubość płyty jest stała i niewielka w porównaniu z
pozostałymi wymiarami,
ugięcia są małe w porównaniu z grubością.
W płytach prostokątnych równomiernie obciążonych momenty zginające przęsłowe i podporowe oblicza się korzystając z tablic.
Tablice opracowano dla następujących schematów statycznych :
Schematy statyczne jednopolowych płyt krzyżowo zbrojonych opartych na czterech krawędziach
Momenty przęsłowe
Ekstremalne momenty zginające w przęsłach oblicza się ze wzorów:
gdzie:
φx, φy - współczynniki z tablic, zależne od ilorazu lx / ly ,
g oraz q - obliczeniowe obciążenie stałe i zmienne.
Momenty podporowe
Oblicza się ze wzorów (analogicznych do wzorów dla płyt jednokierunkowo zginanych)
przy obustronnym zamocowaniu
b) przy jednostronnym zamocowaniu
gdzie: χ - współczynnik z tablic wyrażający proporcjonalność obciążenia w pasmach płyty w kierunkach x oraz y.
Zbrojenie w płytach dwukierunkowo zbrojonych
wymiarowanych zgodnie z teorią sprężystości podaje norma.
Obliczone zbrojenie przęsłowe dla kierunku x oraz y należy układać w strefie środkowej o wymiarach
3/5 lx oraz 3/5 ly .
W pasmach skrajnych 1/5 lx oraz 1/5 ly , pole przekroju zbrojenia może być zmniejszone do połowy.
Obraz zarysowania płyty swobodnie podpartej
równomiernie obciążonej
u góry u dołu
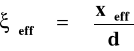
gdzie: xeff - efektywna wysokość
strefy ściskanej przekroju
d - wysokość użyteczna przekroju
W obliczeniach praktycznych nie możemy z góry
określić z jakim przypadkiem przekroju teowego
mamy do czynienia.
Ponieważ nie znamy wysokości strefy ściskanej, przyjmujemy
xeff = hf
Przy tym założeniu obliczamy nośność przekroju
MRd = fcd beff hf (d - 0,5hf )
Moment MRd jaki może przenieść przekrój
przy założeniu xeff = hf porównujemy
z momentem MSd od obciążeń obliczeniowych.
Jeżeli: MSd ≤ MRd to przekrój pozornie teowy (przypadek 1).
Jeżeli: MSd > MRd to przekrój rzeczywiście teowy (przypadek 2).
|
Nośność na ścinanie
Sprawdzenie stanu granicznego nośności na ścinanie
polega na wykazaniu, że na każdym odcinku,
który można wydzielić z elementu
spełniony jest warunek:
VSd ≤ VRd |
|
gdzie:
VSd - wartość bezwzględna obliczeniowej siły
poprzecznej,
VRd - obliczeniowa nośność na ścinanie.
Obliczeniowa nośność na ścinanie VRd jest równa jednej z trzech nośności, które wyznaczają graniczne siły poprzeczne:
VRd1, VRd2 albo VRd2, red, VRd3.
VRd1 - jest to obliczeniowa nośność na ścinanie ze względu na
rozciąganie betonu powstające przy ścinaniu w elemencie
bez zbrojenia poprzecznego,
VRd2 - jest to obliczeniowa nośność na ścinanie ze względu na
ściskanie betonu powstająca przy ścinaniu w elementach
zginananych, a VRd2,red - w elementach mimośrodowo
ściskanych,
VRd3 - jest to obliczeniowa nośność na ścinanie ze względu na
rozciąganie poprzecznego zbrojenia na ścinanie.
VRd1 - nośność na ścinanie w elemencie bez
zbrojenia poprzecznego
VRd2 - nośność na ścinanie betonowych
krzyżulcow ściskanych
VRd3 - nośność na ścinanie zbrojenia
poprzecznego
Objaśniając opisowo poszczególne siły graniczne
można stwierdzić, że:
rozciągająca siła VRd1 powstaje w betonie przy ścinaniu i określa ile może przenieść „sam” beton
na odcinkach gdzie nie ma zbrojenia poprzecznego,
ściskająca siła VRd2 odpowiada maksymalnej nośności ściskanych krzyżulców betonowych,
rozciągająca siła VRd3 określa nośność na ścinanie zbrojenia poprzecznego.
Obliczeniową nośność na ścinanie VRd1 w elemencie , który nie ma zbrojenia poprzecznego na ścinanie wyznacza się ze wzoru
VRd1 = [0,35 k fctd (1,2 + 40ρL) + 0,15 σcp] bw d
gdzie:
bw - najmniejsza szerokość strefy ścinania w przekroju
poprzecznym,
k - współczynnik równy 1,0, gdy do podpory doprowadzono
mniej niż 50% rozciąganego zbrojenia przęsłowego, a w
innych przypadkach wyznaczony ze wzoru
k = 1,6 - d ≥ 1,0
gdzie d oznacza wysokość użyteczną przekroju w metrach,
ρL - stopień zbrojenia określony wzorem
![]()
gdzie:
ASL - pole przekroju głównego zbrojenia rozciąganego mającego długość nie mniejszą niż d + lbd poza rozpatrywanym przekrojem elementu ,
σcp - średnie naprężenie ściskające w betonie, które w elementach żelbetowych wywołane jest przez siłę podłużną NSd , a w elementach sprężonych przez sumę siły podłużnej NSd i podłużnej siły sprężającej Npd wyznaczane ze wzoru
σcp = (NSd + Npd) / Ac ≤ 0,2 fcd
gdzie Ac jest polem poprzecznym przekroju betonu.
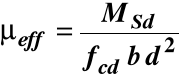
> μeff,lim
Uwzględniając zbrojenie konstrukcyjne
oraz różnego rodzaju zbrojenie pomocnicze
ilość stali nie przekracza na ogół 5 %
fc
![]()
Klasa betonu jest to określenie jakości betonu
odpowiadające jego wytrzymałości gwarantowanej
fck
fcd
fct
![]()
![]()
VSd ≤ VRd1
VRd1 < VSd ≤ VRd2
VSd > VRd2
VRd1
VRd2 (VRd2, red)
0
Vsd
Nie trzeba obliczać
zbrojenia na ścinanie
Zaprojektować zbrojenie
poprzeczne na ścinanie
Zmienić wymiary przekroju
lub klasę betonu.
Przekroju nie można prawidłowo zaprojektować.
Odcinek pierwszego
rodzaju
Odcinek drugiego
rodzaju
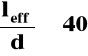
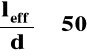
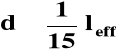
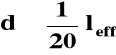
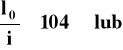
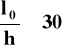
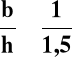
Wyszukiwarka
Podobne podstrony:
PrawoUpadłościoweINaprawcze Wykład zaoczne całość 2012
wyklady socjologia calosc, mgr fizoterapii
Wykłady z filozofii - całość, Pedagogika studia magisterskie, filozofia
Antropologia+k.+wyklady+RULKA+całość
Patologie spoleczne - wyklady poprawione calosc, Patologie społeczne (skrzacik 211)
wykłady społeczna całość, Psychologia
TPL całość wykłady, TPL całość wykłady, TPL
PrawoUpadłościoweINaprawcze Wykład zaoczne całość 2012
wykład 1 wymiary zdrowia
postepowanie administracyjne wyklady calosc
Chemia organiczna wykłady całość(1)
wyklady calosc, analiza instrumentalna
Metody inzynierii genetycznej w hodowli zwierzat wyklady(calosc1)
Derma wyklady calosc, CHOROBY PASOŻYTNICZE SKÓRY, CHOROBY PASOŻYTNICZE SKÓRY
więcej podobnych podstron