LABOLATORIUM FIZYCZNE
Tomasz Różański	grupa C zespół	Data:
Temat: Wyznaczanie momentu bezwładności za pomocą wahadła Oberbecka	ĆWICZENIE nr 5 a,b

OPRACOWANIE TEORETYCZNE:

Niezrównoważony moment siły:

(1)

nadaje bryle sztywnej przyspieszenie kątowe:

(2)

proporcjonalne do tego właśnie momentu:

(3)

Sumowanie iloczynów elementarnych mas m_i i kwadratów ich odległości od osi obrotu należy zastąpić całkowaniem po całej masie bryły:

(5)

Dla ciała jednorodnego o stałej gęstości wzór (5) przyjmuje postać:

(6)

Po uwzględnieniu definicji przyspieszenia kątowego (3.2) oraz momentu pędu (krętu):

(7)

Otrzymujemy uogólnioną postać II zasady dynamiki bryły sztywnej:

(8)

W przypadku gdy oś obrotu nie przechodzi przez środek masy bryły, to obliczając moment bezwładności bryły należy uwzględnić wzór Steinera:

(9)

gdzie I₀- moment bezwładności dla osi przechodzącej przez środek masy ciała S

d- równoległe przesunięcie między tymi osiami

OPIS METODY POMIAROWEJ

Wykorzystujemy tzw. wahadło Oberbecka. Przyrząd ten umożliwia pośredni pomiar przyspieszenia kątowego układu (krzyżaka z obciążnikiem) obracającego się przy różnych ustalonych wartościach momentu bezwładności oraz momentu siły. Zarówno moment bezwładności układu, jak i moment siły przyłożony do krzyżaka możemy zmieniać w sposób skokowy. Moment bezwładności układu zmienia się poprzez przesuwanie tulejki wzdłuż ramion krzyżaka. Moment siły zmieniamy nawijając nitkę na jeden z dwóch krążków, lub zmieniając liczbę ciężarków na szlace obciążnika.

Koło zamachowe wykonane jest w postaci krzyżaka, na którego ramionach znajdują się przesuwane tulei o masie m. Na osi krzyżaka umocowany jest krążek, na którym nawinięto nić przerzuconą przez bloczek. Do drugiego końca nici przywiązujemy szalkę z ciężarkami. Ruch obrotowy krążka z krzyżakiem wywołany jest moment siły:

(10)

gdzie: T₁ - moment sił tarcia dla krążka

r - promień krążka

I -moment bezwładności układu krążka z krzyżakiem i obciążnikami

(11)

gdzie I_o - moment bezwładności krążka z krzyżakiem

m - masa tulejki

d - odległość tulejki od osi obrotu

Z kolei dla górnego bloczka (o momencie bezwładności I₁ i promieniu R ) OI zasada dynamiki ruchu obrotowego wyrażona jest wzorem:

(12)

gdzie: T₂ - moment sił tarcia dla bloczka.

Ciężarek m₀ opada pod wpływem siły ciężkości ruchem jednostajnie przyspieszonym z przyspieszeniem:

(13)

Rozwiązaniem układu tych równań względem przyspieszenia kątowego krążka z krzyżakiem:

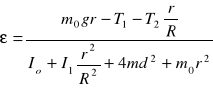
(14)

Dla ruchu jednostajnie przyspieszonego opadającego ciężarka:

(15)

gdzie: h - przebyta droga

t - czas opadania

Stąd mamy:

(16)

Równania (14) i (16) dają ostatecznie związek:

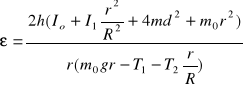
(17)

Wprowadzam oznaczenia:

(18)

(19)

(20)

Wyrażenie (17) przybiera wówczas postać:

(21)

Wyrażenie (21) zapiszmy w postaci:

(22)

gdzie:
(23)

(24)

Współczynniki a i b można obliczyć metodą regresji liniowej. Po wprowadzeniu oznaczeń x=d² i y=t² otrzymamy równanie prostej y=ax+b.

Zaniedbując moment sił tarcia dla górnego bloczka równanie na moment sił tarcia w bloczku przyjmie postać:

(25)

oraz moment bezwładności krzyżaka:

(26)

---