P O L I T E C H N I K A Ś W I Ę T O K R Z Y S K A LABORATORIUM AUTOMATYKI
Ćwiczenie nr: 2		Temat : WYZNACZYĆ CZĘŚĆ UROJONĄ Q(ω) CZŁONU INERCYJNEGO I RZĘDU.
1999/2000 Rok akadem.	V Semestr.		32B Grupa.	Mariusz Tarłowski Arkadiusz Wójcikiewicz Nazwisko i imię studenta	99-10-25 Data.	Ocena.

Człon inercyjny pierwszego rzędu.

Każdy człon jest opisany równaniem różniczkowym:

a zatem o transmitancji:

nazywamy członem inercyjnym pierwszego rzędu. Charakterystyki częstotliwościowe:

• P(ω),

• Q(ω),

• amplitudowo - fazowa G(jω) = P(ω) + jQ(ω),

• logarytmiczne: L(ω) = 20log |G(jω)| i fazowa ϕ(ω) = arg G(jω)

Charakterystyki częstotliwościowe członu inercyjnego pierwszego rzędu

Odpowiedź skokowa h(t) członu inercyjnego wyraża się równaniem:

Na rysunku poniżej pokazane są krzywe h(t) dla trzech różnych wartości stałych czasowych T(T₁<T₂<T₃). Ze wzoru na h(t) wynika, że im mniejsza jest wartość stałej czasowej T, tym szybciej układ dąży do stanu ustalonego. Odpowiedź skokowa członu inercyjnego nie wykazuje przeregulowań, natomiast czas regulacji t_r określony jest z dużym przybliżeniem równością:

t_r = 3T

Stałą czasową T układu inercyjnego można wyznaczyć doświadczalnie mierząc odpowiedź skokową h(t) i określając punkt przecięcia się stycznej poprowadzonej z początku układu współrzędnych, do krzywej h(t) z asymptotą krzywej wykładniczej dla t → ∞. Stałą czasową można również wyznaczyć na podstawie charakterystyki częstotliwościowej. Z zależności:

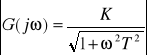
wynika, że ωT = 1,
. Wobec tego, stałą czasową T określamy jako odwrotność pulsacji, dla której |G(jω)| = 0,707K.

Odpowiedź skokowa członu inercyjnego dla T₁<T₂<T₃

STRONA 2

LABOARATORIUM Z AUTOMATYKI

---