Wydział: Chemiczny |
Dzień/godz: wtorek, 8-15 |
Nr zespołu: 2 |
||
|
Data: 18.03.2003 |
|
||
Nazwisko i Imię
|
Ocena z przygotowania:
|
Ocena ze sprawozdania: |
Ocena: |
|
Prowadzący: Marcin Sarzyński |
Podpis prowadzącego:
|
|||
Badanie anharmoniczności drgań wahadła matematycznego
Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła różnicowego
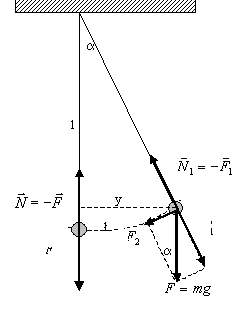
Wahadłem matematycznym płaskim nazywamy punkt materialny poruszający się po łuku w polu grawitacyjnym.
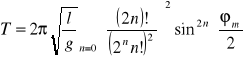
Zależność okresu drgań T wahadła matematycznego od maksymalnego kąta wychylenia ϕm:
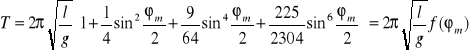
Ze wzoru wynika, że okres drgań wahadła rośnie wraz ze wzrostem maksymalnego wychylenia. Można przyjąć (dla kątów ϕ<π/2), że powyższy wzór ma następującą postać:
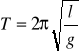
Gdy będziemy zmniejszać wartość kąta, to w końcu przy ϕ→0 okres przestanie zależeć od wychylenia i otrzymamy:
Występują wówczas drgania harmoniczne (siła proporcjonalna do wychylenia). W praktyce, z powodu niedokładności przyrządów pomiarowych przedział wartości ϕ, w którym okres T jest niezależny od wychylenia jest szerszy.
Przyspieszenie ziemskie wygodniej wyliczyć przy pomocy wahadła różnicowego, w celu zminimalizowania błędów pomiaru długości. Używając wahadła matematycznego, przeprowadza się kilka eksperymentów dla różnej długości (a tego samego kąta maksymalnego wychylenia), a następnie przeprowadza wyliczenia dla różnicy długości, którą można zmierzyć o wiele precyzyjniej.
Tak więc dla długości l0 okres drgań będzie:
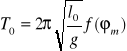
zaś dla innej mniejszej długości li będzie krótszy i wyniesie:
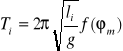
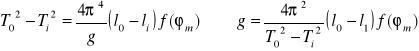
Podnosząc oba równania do kwadratu i odejmując stronami po przekształceniach otrzymamy:
Wyniki:
Układ pomiarowy:
Eksperymenty przeprowadzaliśmy przy pomocy statywu wahadła o regulowanym punkcie górnego zaczepienia, wahadła przybliżającego matematyczne oraz elektronicznego układu pomiarowego składającego się z fotokomórki i podłączonego do niej miernika czasu. Mierzyliśmy długość jednego półokresu.
Anharmonicznośc drgań wahadła:
Przeprowadziliśmy serię pomiarów dla każdej wartości kąta początkowego wychylenia od 5 do 50 stopni, po 4 pomiary półokresów. Następnie z każdej takiej czwórki wyciągnęliśmy średnią. Błąd pomiaru kąta oceniamy na 5 stopni, błąd pomiaru czasu każdego eksperymentu oceniamy na 0,001sekundy, co daje nam bezwzględną niepewność pomiarową ΔT = 1⋅10-3s.
Wartość f(φm) jest funkcją zmiennej φm obarczonej błędem pomiarowym Δφm = 5°:
![]()
Bezwzględna niepewność wielkości będącej funkcją jednej zmiennej równa jest bezwzględnej niepewności wielkości mierzonej pomnożonej przez pochodną funkcji:
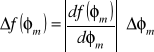
![]()
Oto wyniki jakie otrzymaliśmy w kolejnych próbach z uwzględnieniem długości nici:
L = 50 cm
ϕm [stopnie] |
Średnie T [s] |
f(ϕm) |
Δf(ϕm) |
5 |
1, 716 |
1,000476 |
0,003134 |
10 |
1, 72 |
1,0019072 |
0,006245 |
20 |
1, 73 |
1,007669 |
0,0123 |
30 |
1, 744 |
1,017407 |
0,017982 |
40 |
1, 776 |
1,031325 |
0,023117 |
50 |
1, 798 |
1,039934 |
0,02543 |
Wykres nr 1
L = 40 cm
ϕm [stopnie] |
Średnie T [s] |
f(ϕm) |
Δf(ϕm) |
5 |
1, 602 |
1,000476 |
0,003134 |
10 |
1, 598 |
1,0019072 |
0,006245 |
20 |
1, 604 |
1,007669 |
0,0123 |
30 |
1, 614 |
1,017407 |
0,017982 |
40 |
1, 634 |
1,031325 |
0,023117 |
50 |
1, 666 |
1,039934 |
0,02543 |
Wykres nr 2
L = 30 cm
ϕm [stopnie] |
Średnie T [s] |
f(ϕm) |
Δf(ϕm) |
5 |
1, 456 |
1,000476 |
0,003134 |
10 |
1, 466 |
1,0019072 |
0,006245 |
20 |
1, 472 |
1,007669 |
0,0123 |
30 |
1, 488 |
1,017407 |
0,017982 |
40 |
1, 506 |
1,031325 |
0,023117 |
50 |
1, 532 |
1,039934 |
0,02543 |
Wykres nr 3
L = 20 cm
ϕm [stopnie] |
Średnie T [s] |
f(ϕm) |
Δf(ϕm) |
5 |
1, 318 |
1,000476 |
0,003134 |
10 |
1, 320 |
1,0019072 |
0,006245 |
20 |
1, 326 |
1,007669 |
0,0123 |
30 |
1, 338 |
1,017407 |
0,017982 |
40 |
1, 356 |
1,031325 |
0,023117 |
50 |
1, 382 |
1,039934 |
0,02543 |
Wykres nr 4
Obliczanie wartości przyspieszenia ziemskiego:
Przyspieszenie ziemskie obliczamy za pomocą wahadła różnicowego. Wykonaliśmy serię pomiarów dla różnej długości wahadła. Błąd pomiaru długości nici wahadła wynosił 0,001 m. Błędy pomiaru czasu wynoszą 0,001 sekundy
![]()
Pozwala to na wyliczenie wartości g z wzoru:
gdzie ![]()
Po przekształceniu otrzymujemy: 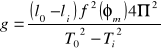
Dla naszych wartości otrzymaliśmy wynik 9,82 [m/s2]
Błąd pomiaru wartości przyspieszenia liczymy ze wzoru:![]()
gdzie: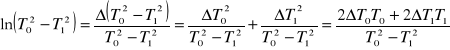
![]()
![]()
Otrzymana wartość obarczona jest błędem: ![]()
Wartość przyspieszenia ziemskiego wraz z błędem wynosi 9,82 [m/s2]![]()
0,11 [m/s2]
Wnioski:
Teoretycznie okres drgań wahadła matematycznego prostego nie powinien zależeć od amplitudy wahań o czym mówi własność izochronizmu, jednak doświadczalnie okres drgań proporcjonalnie rośnie wraz ze wzrostem amplitudy. Nazywamy to zjawiskiem anharmoniczności drgań wahadła. Natomiast zarówno teoretycznie jak i doświadczalnie zależy od długości nici.
.
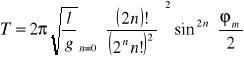
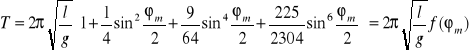
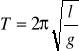
![]()
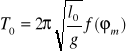
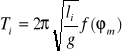
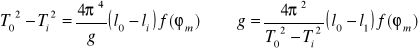
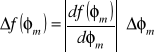
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Lab Fiz322a, Studia, II rok, Fizyka Eksperymentalna
Spr z fizy 31, Studia, II rok, Fizyka Eksperymentalna
Spr 42, Studia, II rok, Fizyka Eksperymentalna
Fizyka1, Studia, II rok, Fizyka Eksperymentalna
Cwiczenie 19, Studia, II rok, Fizyka Eksperymentalna
protokół fiza, Studia, II rok, Fizyka Eksperymentalna
Spr z fizy 35, Studia, II rok, Fizyka Eksperymentalna
FIZLAB~1, Studia, II rok, Fizyka Eksperymentalna
Spr 34, Studia, II rok, Fizyka Eksperymentalna
sprawozdanie z Halla, Studia, II rok, Fizyka Eksperymentalna
magnetyzm-nasze sprawko;), Studia, II rok, Fizyka Eksperymentalna
fiza, Studia, II rok, Fizyka Eksperymentalna
Lab Fiz364j, Studia, II rok, Fizyka Eksperymentalna
więcej podobnych podstron