Pomiar stałej dielektrycznej skał.
Podstawy fizyczne:
Jedną z wielu fizycznych własności wykorzystywanych w warunkach laboratoryjnych do analizy próbek skał jest stała dielektryczna ε . Własność ta jest miarą podatności badanej próbki na polaryzację zewnętrznym polem elektrycznym kształtującą wewnętrzną strukturę elektryczną w postaci dipoli, czyli przesuniętych względem siebie ładunków dodatnich i ujemnych. Zjawisko polaryzacji można sobie wyobrazić jako działanie łańcuchów dipolowych formowanych pod wpływem przyłożonego pola wewnętrznego o natężeniu Ez. Przesunięcia ładunków powodują indukowanie się na przeciwległych powierzchniach próbki ładunków powierzchniowych przeciwnego znaku o potencjale U.
U= Ew * l
gdzie:
Ew - średnie przestrzenne natężenie pola elektrycznego wewnątrz próbki
l - uśredniona odległość ładunków powierzchniowych
Analizując makroskopowo zachowanie się próbki dielektrycznej w zewnętrznym polu elektrycznym Ez jako elementu biernego, tzn. nie wnoszącego wkładu w natężenie pola, należy założyć niezmienność wartości potencjału ładunków powierzchniowych U, czyli natężenia pola zewnętrznego Ez związanego z polem wewnętrznym Ew relacją
Ez = ε * Ew
gdzie:
ε-współczynnik proporcjonalności będący miarą podatności badanej próbki na polaryzację, zwany stałą dielektryczną
Stała dielektryczna jest jedną z wielu fizycznych własności którą to wykorzystuje się do badania próbek w zewnętrznym polu elektrycznym, kształtującą wewnętrzną strukturę elektryczną w postaci dipoli.
Przenikalność dielektryczną próżni wynosi:
ε0 - 8,854 * 10-12 [-]
Stałą dielektryczną ε określamy z przyrostu pojemności wzorem:
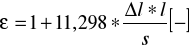
gdzie: Δc- różnica pojemności kondensatora zawierającego między okładkami badanej próbki cd i pojemności kondensatora pustego co Δc= cd- co
l- odległość między elektrodami kondensatora
s- powierzchnia próbki
Elektryczne i elektromagnetyczne własności skał zależy od :
składu chemicznego oraz mineralnego skały
składu nasycających je faz ciekłych
częstotliwości pola polaryzującego
temperatury badanej próbki
kształtu i orientacji cząstek elektrycznych
gęstości
Przeprowadzenie ćwiczenia:
Badaną próbkę umieszczamy w uchwycie pomiarowym tworzącym kondensator, którego okładki połączymy kablem do zacisków pomiarowych. Po zmierzeniu pojemności kondensatora z badaną próbką dla czterech częstotliwości identycznie obliczenia wykonujemy dla kondensatora pustego (bez badanej próbki).
Stałe dielektryczne obliczamy ze wzoru:
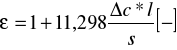
zaś błąd pomiaru stałej dielektrycznej liczymy wykorzystując prawo przenoszenia błędów:
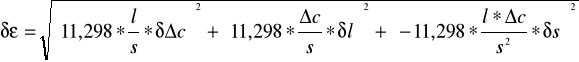
gdzie:
δl = 0,01[cm]
δs = 0,01[cm2]
δc= 2 [pF}
Wyniki dla próbki 11:
Pomiar pojemności w [pF] przy częstotliwości [Hz] |
||||
|
10 kHz |
100 kHz |
1 MHz |
10 MHz |
Przyrost pojemności ΔC [pF] |
22 |
15 |
13 |
11 |
ε [-] |
1,872 |
1,046 |
1,0021 |
8,092*10-5 |
δε |
2,8*10-6 |
|
|
|
Wyniki dla próbki 30A
Pomiar pojemności w [pF] przy częstotliwości [Hz] |
||||
|
10 kHz |
100 kHz |
1 MHz |
10 MHz |
Przyrost pojemności ΔC [pF] |
134 |
64 |
28 |
13 |
ε [-]b |
|
|
|
|
δε |
|
|
|
|
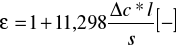
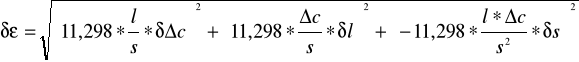
Wyszukiwarka
Podobne podstrony:
pomiar stałej dielektr skał
Pomiar stałej dielektrycznej skał 4, AGH WGGIOŚ, Semestr 3, Metody Badań Geofizycznych
POMIAR STAŁEJ CZASOWEJ
Pomiar stałej siatki dyfrakcyjnej za pomocą spektrometru a, POLITECHNIKA CZ˙STOCHOWSKA
Pomiar stałej siatki dyfrakcyjnej za pomocą spektrometru, 17-stała siatki dyfrakcyjnej
POMIAR STAŁEJ SIATKI DYFRAKCYJNEJ ZA POMOCĄ SPEKTROMETRU (2)
7 POMIAR STALEJ CZASOWEJ TERMOELEMENTU
MATERIAŁOZNAWSTWO ELEKTRYCZNE Pomiary przenikalności dielektrycznej materiałów elektroizolacyjnych
Pomiar stałej siatki dyfrakcyjnej za pomocą spektrometru (3), Sprawozdania - Fizyka
19 sprawko, Studia, Pracownie, I pracownia, 19 Pomiar stałej grawitacyjnej G (ważenie Ziemi), 19 - n
w2, Stała Plancka, W2 - Pomiar stałej Plancka z wykorzystaniem zewnętrznego zjawiska fotoelektryczne
Opt- Pomiar stałej Siatki Dyfrakcyjnej za Pomocą Spektrometr, Sprawozdania - Fizyka
Pomiar stałej siatki dyfrakcyjnej za pomocą spektrometru, Sprawozdania - Fizyka
Pomiar przenikalności dielektrycznej względnej materiałów izolacyjnych, ?wiczenie
MATERIAŁOZNAWSTWO ELEKTRYCZNE Pomiar stratności dielektryków ciekłych mostkiem RLC
pomiar stalej czasowej termoel
pomiar stałej siatki dyfrakcyjnej za pomocą światła laserowego (2)
MATERIAŁOZNAWSTWO ELEKTRYCZNE Pomiar przenikalności dielektrycznej względnej materiałów izolacyjny
więcej podobnych podstron