Materiały pomocnicze do egzaminu z PODSTAW MATEMATYKI

(II część)

1. Pojęcie macierzy. Wymiar macierzy. Rodzaje macierzy.

2. Działania na macierzach.

3. Mnożenie wektora-wiersza przez wektor-kolumnę. Mnożenie r-wymiarowego wektora-kolumnę przez r-wymiarowy wektor-wiersz.

4. Macierze: transpozycja macierzy, macierz osobliwa, macierz nieosobliwa, macierz odwrotna, macierz Grama.

5. Wyznaczniki macierzy kwadratowych: osobliwej, nieosobliwej. Obliczanie wartości wyznaczników (schemat Sarrusa). Wyznaczniki macierzy stopnia wyższego od 3. Minor, dopełnienie algebraiczne, wzory Laplace'a.

6. Rząd macierzy. Wykorzystywanie macierzy Grama do obliczania rzędu macierzy.

7. Układ równań liniowych. Układy Cramera. Wyznaczanie pierwiastków układu równań Cramera.

8. Układy równań liniowych jednorodnych. Zerowe i niezerowe pierwiastki układu równań liniowych.

9. Zagadnienie istnienia rozwiązań układu równań liniowych. Zastosowania rzędu macierzy do badania istnienia rozwiązań układu równań.

10. Macierzowy zapis układu równań liniowych.

11. Przykłady działań na macierzach.

1. Dane są macierze:
   ,
   .

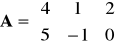
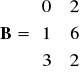
Oblicz:
;
;
;
;
.

2. Wykonaj mnożenie:

12. Obliczanie wartości wyznaczników macierzy stopnia 3 i wyższego od 3.

a)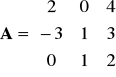
,

b)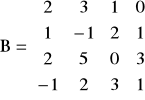
,

Uwaga: Zastosować rozwinięcia Laplace'a.

13. Znaleźć macierz odwrotną do macierzy:

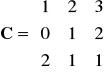
1. Jakie warunki musi spełniać macierz C?

2. Wykorzystać wzór:
   

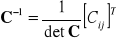
przy czym C_ij jest dopełnieniem algebraicznym elementu c_ij macierzy C.

14. Zbadać czy układy wektorów są liniowo niezależne:

a)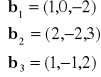
b)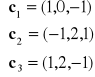

15. Rozwiązać układ równań:

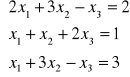
Sprawdź, czy jest to układ Cramera. Jeżeli tak, to dlaczego? Jeżeli nie, to dlaczego? W zależności od odpowiedzi zastosować odpowiednią procedurę obliczeniową.

16. Co można powiedzieć o dowolnej części liniowo niezależnego układu wektorów?

17. Liniowo niezależny układ wektorów nie zawiera wektora zerowego. Dlaczego?

18. Macierzową postać układu równań liniowych można zapisać w następujący sposób:

, (1)

gdzie

A jest macierzą, której elementami są współczynniki stojące przy niewiadomych układu równań,

x -wektor kolumnowy o składowych x_i,

b - wektor kolumnowych o składowych, będących wyrazami wolnymi rozpatrywanego układu.

1. Rozwiązaniem tego układu jest ……………………….., zapisane macierzowo.

2. Jakie wymiary muszą mieć poszczególne człony układu (1), aby działanie było wykonalne?

2

---