Tatiana Zaszkowska 28 III 2001
Ćwiczenie nr 5
Temat: Badanie ruchu obrotowego bryły sztywnej i wyznaczanie momentu bezwładności przyrządu - wahadło Oberbecka.
Tabela pomiarów:
Teoria:
Pierwsza zasada dynamiki ruchu obrotowego
Bryła sztywna nie poddana działaniu momentu siły pozostaje nieruchoma lub wykonuje ruch obrotowy jednostajny.
Druga zasada dynamiki ruchu obrotowego
Bryła, na którą działa moment siły porusza się ruchem obrotowym przyspieszonym. Zatem moment siły działającej na bryłę sztywną jest równy iloczynowi momentu bezwładności I tej bryły i jej przyspieszenia kątowego.
![]()
Trzecia zasada dynamiki ruchu obrotowego
Jeżeli na bryłę A działa bryła B pewnym momentem siły, to bryła B działa na A momentem równym co do wartości, lecz o przeciwnym znaku.
Zasada zachowania pędu
Jeżeli moment sił działających na bryłę jest równy 0, to pęd jest zachowany.
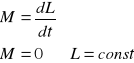
Momentem bezwładności bryły względem danej osi nazywamy sumę iloczynów mas poszczególnych punktów bryły i kwadratów ich odległości od danej osi.
![]()
Opis metody:
Wahadło Oberbecka ma kształt krzyżaka, na którego ramionach osadzone są walce. Na oś krzyżaka o promieniu r nawija się sznurek. Na końcu sznurka zamocowany jest ciężarek o masie m. Mierząc czas opadania ciężarka na drodze h wyznaczamy moment bezwładności ze wzoru:
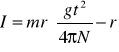
Moment siły działającej na oś krzyżaka jest równa iloczynowi siły naciągu nici i promienia osi. Jest równy także z II zasady dynamiki iloczynowi momentu bezwładności i przyspieszenia kątowego.
![]()
, gdzie ![]()
Zatem:![]()
Ciężarek opada pod wpływem siły ciężkości ruchem jednostajnie przyspieszonym. Całkowita siła działająca na ciężarek wynosi: ![]()
oraz ![]()
.
Wysokość można wyrazić jako długość sznurka owiniętego N razy na osi o promieniu r:
![]()
Podstawiając otrzymujemy powyższy wzór roboczy.
Obliczenia:
Średni promień walca:
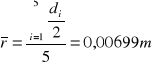
Moment bezwładności przyrządu:
![]()
SZACOWANIE NIEPEWNOŚCI POMIARÓW
Niepewność całkowita dla m:
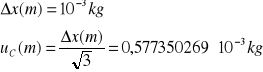
Niepewność całkowita dla r:
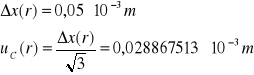
Niepewność całkowita dla g:
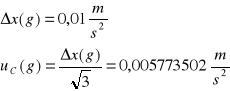
Niepewność całkowita dla t:
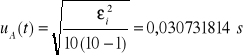
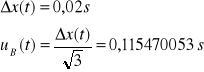
![]()
Wartości pochodnych cząstkowych I względem poszczególnych zmiennych:
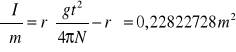
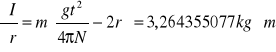
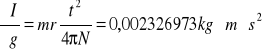
![]()
Niepewność całkowita dla I:
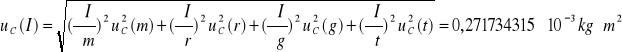
Niepewność rozszerzona ( dla ![]()
=0,95 k=2 ) wynosi:
![]()
Ostateczny wynik :
![]()
Wnioski:
Z wykresu zależności N ( t2 ) wynika, że ciężarek opadał ruchem jednostajnie prostoliniowym ze stałym przyspieszeniem a. Wartość przyspieszenia jest równa tangensowi kąta nachylenia prostej do osi OX. Można ją obliczyć ze stosunku ![]()
do ![]()
. Niektóre punkty na wykresie nie należą do prostej. Wynika to być może z tego, że czasy opadania ciężarka zostały zmierzone niedokładnie.
![]()
Wyszukiwarka
Podobne podstrony:
laborka na za tydzień, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
WYZNACZANIE CIEP A MOLOWEGO, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
01, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
PR FALI, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
NAPI C 1, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
Ćw 12 a, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
Wyznaczanie równoważnika elektrochemicznego miedzi, laboratorium fizyczne, Laboratorium semestr 2 RÓ
37 - wersja 1, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
CPCV, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
Ćw. 1, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
Wahadło torsyjne, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
teoria do 6, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
ćw 5, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
fiz. 1, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
więcej podobnych podstron