Jednokierunkowa analiza wariancji

Pierwsze spojrzenie

Meteorolog postawi sobie pytanie, czy temperatura powietrza zależy od ukształtowania powierzchni? Ekonomista może dociekać czy istnieje istotny związek pomiędzy wysokością zarobków a wykształceniem? Studenci mogą chcieć zbadać czy liczba punktów uzyskane na egzaminie różnią się istotnie między poszczególnymi grupami. Czytając uważnie powyższe pytania i zawarte w nich problemy badawcze powstaje dylemat, jak uzyskać odpowiedź na te zagadnienia, która będzie wiarygodna? Jakie dane zebrać, jak je uporządkować i jakim narzędziem się posłużyć, aby analiza nie okazała się bezowocna?

Przywołajmy raz jeszcze pierwsze pytanie i niech to będzie nasz problem badawczy.

Problem badawczy

Czy temperatura zależy od ukształtowania powierzchni?

Analiza problemu ujawnia dwie wielkości czyli zmienne: temperaturę oraz ukształtowanie powierzchni. Pierwsza ze zmiennych jest wyrażona za pomocą stopni Celsjusza lub Fahrenheit'a. Możemy zatem powiedzieć, iż jeśli zmienna jest wyrażona liczbą, np. jest to temperatura to mamy do czynienia ze zmienną ilościową. Druga zmienna jest wyrażona za pomocą opisu, gdzie opisem jest rodzaj ukształtowania powierzchni, np. nizinny, pagórkowaty, wyżynny, górzysty. Wówczas mamy do czynienia ze zmienną jakościową.

Ponadto, gdy uważnie przeczytamy pytanie zauważymy, iż jedna ze zmiennych zależy od drugiej. To ważny fakt, który prowadzi do rozróżnienia zmiennej zależnej oraz zmiennej niezależnej.

W modelu jednokierunkowej analizy wariancji zmienna zależna oraz zmienna niezależna mają specyficzną nazwę, odpowiednio: replikacja oraz czynnik. W naszej analizie zależności temperatury od ukształtowania powierzchni: czynnik ma 4 poziomy - rodzaje ukształtowania powierzchni, natomiast, replikacje to temperatury przy odpowiednim poziomie czynnika.

Dane

Chcąc przeprowadzić badanie modelem jednokierunkowej analizy wariancji potrzeba zebrać odpowiednie dane. W przypadku naszego problemu badawczego należy zebrać dane dotyczące temperatury oraz ukształtowania powierzchni. Takie dane prezentuje poniższa tablica.

Tablica 1. Dane empiryczne.

Ukształtowanie powierzchni
nizinne	pagórkowate	wyżynne	górzyste
9	8	9	3
11	12	8	5
8	11	6	8
7	8	11	9
6	7	10	7
10	8	10	6
6	9	8	10

Źródło: Onet.pl

FAKT 1

W modelu jednokierunkowej analizy wariancji występują dwie zmienne:

• zmienna ilościowa zależna - replikacja

• zmienna jakościowa niezależna - czynnik

FAKT 2

W modelu jednokierunkowej analizy wariancji:

• liczba poziomów czynnika powinna wynosić co najmniej 3

• liczba replikacji przy każdym poziomie czynnika powinna wynosić co najmniej 5

• liczba replikacji nie musi być taka sama przy różnych poziomach czynnika

Kilka istotnych faktów

Prowadząc badanie metodą jednokierunkowej analizy wariancji trzeba wiedzieć, iż mamy do czynienia z narzędziem ekonometrycznym, modelem, który wymaga spełnienia pewnych wymagań formalnych. Ich niespełnienie może prowadzić do błędnych wniosków wynikających z modelu, a w konsekwencji do podjęcia błędnych decyzji. Ponadto, poznanie istoty modelu znacznie ułatwia pracę badawczą i zwiększa efektywność naszej pracy, a co za tym idzie oszczędzamy czas. Prześledźmy istotne fakty związane z modelem jednokierunkowej analizy wariancji.

1. Model jednokierunkowej analizy wariancji to test statystyczny.

2. Testujemy wartości średnie za pomocą testu F.

3. Średnie są obliczane z wartości znajdujących się w każdym z poziomów czynnika, tj. występuje tyle średnich, ile poziomów czynnika.

4. W modelu analizy wariacji stawiamy dwie hipotezy:

Hipoteza zerowa

• hipoteza zerowa, mówi, iż nie ma istotnych różnic pomiędzy średnimi, a więc czynnik nie wpływa istotnie na wartości średnie analizowanego zjawiska, co jest wyrażone poprzez zapis

W oparciu o analizowany przykład:

Interpretacja hipotezy zerowej jest następująca:

• ukształtowanie terenu nie wpływa istotnie na temperaturę

lub alternatywnie

- różnice pomiędzy średnimi nie są istotne statystycznie

Hipoteza alternatywna:

• hipoteza alternatywna, mówi, iż występują istotne różnice pomiędzy przynajmniej jedną dowolną parą średnich co zapisujemy

W oparciu o analizowany przykład:

Interpretacja hipotezy alternatywnej jest następująca:

• ukształtowanie terenu wpływa istotnie na temperaturę

lub alternatywnie

- różnice pomiędzy średnimi są istotne statystycznie

5. Postawienie hipotez statystycznych oznacza przyjęcie poziomu istotności testu statystycznego, w celu weryfikacji hipotezy zerowej. Jest to prawdopodobieństwo z jakim możemy się mylić odrzucając hipotezę zerową. Ta `pomyłka' jest nazywana błędem pierwszego rodzaju i oznacza przez
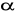
   . Jest oczywistym, iż chcemy się `mylić' niewiele i dlatego z reguły przyjmuje się poziom istotności testu na poziomie 0,05.

6. Zasadniczo jednokierunkowa analiza wariancji opiera się na badaniu dwóch rodzajów zróżnicowania. Pierwszy rodzaj to zróżnicowanie międzygrupowe, drugi rodzaj to zróżnicowanie wewnątrzgrupowe. Badanie zróżnicowania międzygrupowego jest przeprowadzane za pomocą formuły:

o liczbie stopni swobody r - 1.

Badanie zróżnicowania wewnątrzgrupowego jest przeprowadzane za pomocą formuły:

o liczbie stopni swobody n - r.

Powyższe dwie formuły pozwalają na wyprowadzenie wzoru na zróżnicowanie całkowite:

lub

o liczbie stopni swobody n - 1.

gdzie:
- k-ta replikacja przy i-tym poziomie czynnika

- średnia z replikacji przy i-tym poziomie czynnika

- średnia ze wszystkich replikacji

- liczba replikacji przy i-tym poziomie czynnika

- liczba poziomów czynnika

- liczba replikacji (obserwacji) ogółem

Weryfikacja hipotezy zerowej odbywa się z zastosowaniem testu F o formule:

gdzie: MSB oraz MSE to średnie kwadraty odchyleń odpowiednio dla zróżnicowania międzygrupowego oraz zróżnicowania wewnątrzgrupowego wyrażone:

gdzie:
- liczba poziomów czynnika,

- liczba replikacji (obserwacji) ogółem

Obliczenie wartości testu F z próby oraz wyznaczenie wartości krytycznej testu F_α dla przyjętego poziomu istotności
oraz stopni swobody r-1 i n-r pozwala na podjęcie jednej z dwóch następujących decyzji, co do hipotezy zerowej:

• jeśli
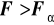
  wtedy odrzucamy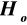
  na korzyść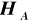
  , co oznacza, iż różnice pomiędzy średnimi są istotne statystycznie

• jeśli
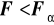
  wtedy nie ma podstaw do odrzucenia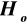
  , co oznacza, iż różnice pomiędzy średnimi nie są istotne statystycznie

Podejmowanie decyzji odnośnie powyższych hipotez statystycznych może mieć miejsce również z wykorzystaniem próbkowego poziomu istotności, tj. wartości-p (p-value).

Przeprowadzając analizę z wykorzystaniem Excel'a odnajdujemy wartość-p i zamieniamy ją na format procentowy.

Decyzje są następujące:

- Jeśli wartość-p jest mniejsza niż 5 procent (poziom istotności, czyli Alfa) odrzucamy
na korzyść
, co oznacza, iż różnice pomiędzy średnimi są istotne statystycznie.

- Jeśli wartość-p jest większa niż 5 procent (poziom istotności, czyli Alfa) wtedy nie ma podstaw do odrzucenia
, co oznacza, iż różnice pomiędzy średnimi nie są istotne statystycznie.

7. Dla wiarygodności modelu niezbędne jest spełnienie założenia zwanego homoskedastycznością. Założenie to oznacza równość, stałość wariancji we wszystkich wyznaczonych przez badacza grupach. Grup jest zawsze tyle ile poziomów czynnika. W omawianym przykładzie są 4 grupy, gdyż zostały przyjęte 4 poziomy czynnika: nizinny, pagórkowaty, wyżynny, górski.

8. Sprawdzanie założenia homoskedastyczności oznacza postawienie dwóch hipotez badawczych:

Hipoteza zerowa

• hipoteza zerowa, mówi, iż nie ma istotnych statystycznie różnic pomiędzy wariancjami w grupach i jest to wyrażone przez formułę

W oparciu o analizowany przykład:

Interpretacja hipotezy alternatywnej jest następująca:

• różnice pomiędzy wariancjami w grupach nie są istotne statystycznie

Hipoteza alternatywna:

• hipoteza alternatywna, mówi, iż pomiędzy przynajmniej jedną dowolną parą wariancji występują istotne różnice, co zapisujemy

W oparciu o analizowany przykład:

Interpretacja hipotezy alternatywnej jest następująca:

- różnice pomiędzy wariancjami w grupach są istotne statystycznie

9. Badanie homoskedastyczności jest przeprowadzane za pomocą dwoma sposobami:

• regułą Hartley'a

• testem Bartlett'a

Reguła Hartley'a

Reguła Hartley'a jest zwana również regułą `kciuka'. Jest to prosta i szybka, aczkolwiek mało wiarygodna metoda zbadania założenia homoskedastyczności modelu jednokierunkowej analizy wariancji. Oparta jest na następującym wzorze:

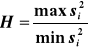
gdzie:
- maksymalna wariancja pośród i-tych poziomów czynnika

- minimalna wariancja pośród i-tych poziomów czynnika

Obliczenie wartości H z powyższego wzoru pozwala na dalsze wnioskowanie co do spełnienia, bądź też odrzucenia założenia. Porównujemy tę wartość z liczbą 9 i postępujemy następująco:

• jeśli
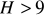
  wówczas odrzucamy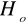
  na korzyść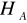
  , co oznacza, iż nie ma stałości wariancji w grupach, czyli model jednokierunkowej analizy wariancji nie spełnia założenia homoskedastyczności

• jeśli
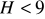
  wówczas nie ma podstaw do odrzucenia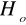
  , co oznacza, iż istnieje stałość wariancji w grupach, czyli model jednokierunkowej analizy wariancji spełnia założenia homoskedastyczności

Test Bartlett'a

Test Bartlett'a jest to wiarygodna metoda zbadania założenia homoskedastyczności modelu jednokierunkowej analizy wariancji. Oparta jest na następującej statystyce:

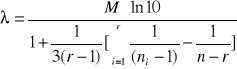
przy czym:

gdzie:
- liczba poziomów czynnika,

- liczba replikacji (obserwacji) ogółem

- liczba replikacji przy i-tym poziomie czynnika

- wariancja przy i-tym poziomie czynnika (w każdej z grup)

Statystyka
ma rozkład
o liczbie stopni swobody r - 1.

Obliczenie wartości
i porównanie jej z wartością krytyczną rozkładu
daje podstawy do wnioskowania o spełnieniu założenia homoskedastyczności przez model jednokierunkowej analizy wariancji. Rozpatrzmy dwie następujące sytuacje:

• jeśli
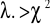
  wówczas odrzucamy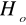
  , co oznacza, iż nie ma stałości wariancji w grupach, czyli model jednokierunkowej analizy wariancji nie spełnia założenia homoskedastyczności

• jeśli
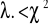
  wówczas nie ma podstaw do odrzucenia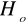
  , co oznacza, iż istnieje stałość wariancji w grupach, czyli model jednokierunkowej analizy wariancji spełnia założenia homoskedastyczności

Test Bartletta może być przeprowadzony z wykorzystaniem makra ANOVA.xls.

Interpretacja wyników uzyskanych z makra jest następująca:

Jeśli wartość-p będzie mniejsza niż 5 procent, wówczas odrzucamy
i model nie spełnia założenia homoskedastyczności.

Jeśli wartość-p będzie większa niż 5 procent; wówczas nie ma podstaw do odrzucenia
i model spełnia założenia homoskedastyczności.

10. W przypadku, gdy model nie spełnia założenia homoskedastyczności, tj. nie istnieje stałość wariancji w grupach konieczna jest transformacja danych empirycznych. Oczywistym jest, iż przekształcenie to dotyczy zmiennej zależnej tj. replikacji, gdyż ma ona charakter ilościowy. Dopuszczalne są dwa rodzaje transformacji: logarytmiczna oraz potęgowa.

Logarytmiczna transformacja polega na wyznaczeniu dla każdej z replikacji jej logarytmu, naturalnego bądź dziesiętnego.

Odnosząc się do naszego przykładu replikacje po transformacji logarytmem naturalnym będą miały postać:

Tablica 3. Dane po zlogarytmowaniu.

Ukształtowanie powierzchni
Nizinne	Pagórkowate	Wyżynne	Górzyste
2,197	2,079	2,197	1,099
2,398	2,485	2,079	1,609
2,079	2,398	1,792	2,079
1,946	2,079	2,398	2,197
1,792	1,946	2,303	1,946
2,303	2,079	2,303	1,792
1,792	2,197	2,079	2,303

Źródło: Obliczenia własne na podstawie Tablicy 1.

Transformacja potęgowa polega na podniesieniu każdej z replikacji do dowolnej potęgi o wykładniku z przedziału (0,1)

Odnosząc się do naszego przykładu replikacje po transformacji potęgowej będą miały postać:

Tablica 4. Dane po transformacji potęgowej o wykładniku 0,2

Ukształtowanie powierzchni
Nizinne	Pagórkowate	Wyżynne	Górzyste
1,55	1,515	1,551	1,245
1,615	1,643	1,515	1,379
1,515	1,615	1,430	1,515
1,475	1,515	1,615	1,551
1,430	1,475	1,584	1,475
1,584	1,515	1,584	1,430
1,430	1,551	1,515	1,584

Źródło: Obliczenia własne na podstawie Tablicy 1.

Po zabiegu transformacji wartości replikacji przy analizowanych 4 poziomach czynnika uległy spłaszczeniu. Po drugie, obserwujemy, iż wartości są zbliżone do siebie. Taka sytuacja jest pożądana, gdyż wartości wariancji w badanych grupach ulegną zmniejszeniu.

Do `nowych replikacji' tj. replikacji po transformacji należy ponownie zastosować model jednokierunkowej analizy wariancji oraz ponownie zweryfikować założenie modelu, tj. homoskedastyczność.

Porównania wielokrotne

W przypadku, gdy w modelu jednokierunkowej analizy wariancji została odrzucona hipotez zerowa o równości wszystkich średnich powstaje pytanie która lub które ze średnich wpłynęły na taką decyzję. Aby to wykazać wykorzystujemy metodę nazywaną porównaniami wielokrotnymi, gdzie pytamy o istotność różnic pomiędzy poszczególnymi parami średnich. Ponadto technika porównań wielokrotnych daje możliwość wskazania skrajnych wartości średnich.

Badanie różnic między parami średnich można zapisać jako weryfikację hipotezy:

Zastosujemy procedurę: najmniejszej istotnej różnicy (czyli LSD) o formule:

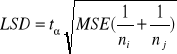
gdzie:

natomiast do weryfikacji czy różnica między parami średnich jest statystycznie istotna wykorzystamy procedurę:

i jeśli teraz dla dwóch średnich zachodzi powyższa relacja powiemy, iż różnica między tymi średnimi jest statystycznie istotna.

LSD można przeprowadzić używając do tego makra ANOVA.xls.

Jak odczytać wyniki?

	ISTOTNOŚĆ RÓŻNIC
	1	2	3	4
1
2	1
3	1	0
4	1	0	0

Cyfry oznaczone na kolor czerwony oznaczają średnie w grupach, które są z sobą porównywane. Jeśli na przecięciu danych grup, np. grupy 1 oraz 2 będzie „jedynka” różnice jakie występują pomiędzy średnimi są statystycznie istotne i nie wolno połączyć tych grup razem. Jeśli na przecięciu danych grup, np. grupy 2 oraz 3 będzie „zero” różnice jakie występują pomiędzy średnimi nie są statystycznie istotne i można połączyć te grupy razem.

Wobec tego, na mocy powyższego opisu można utworzyć z 4 grup (1,2,3,4) dwie grupy, tj. {1} oraz {2,3,4}.

---