Zadanie II.13. Adam Parulski WM.32.

W zbiorniku otwartym o zasobie objętości V=10[m³] wypełnionym powietrzem traktowanym tak jak gaz doskonały o początkowych parametrach stanu ciśnienia p₁=0,1[Mpa] i temperaturze T₁=300[K] po doprowadzeniu w przemianie termodynamicznej odwracalnej przyrostu ilości ciepła ΔQ temperatura wzrosła do T₂=400[K]. Obliczyć przyrost ilości ciepła ΔQ doprowadzonego do zbiornika wiedząc, że wykładnik adiabaty k=1,4.

Dane: Szukane:

V=10[m³] ΔQ=?

P₁=0,1[Mpa]

T₁=300[K]

T₂=400[K]

K=1,4

1.Rysunek:

2. Wykresy P-V i T-S.

3. Bilans zasobu energii wewnętrznej dla układu otwartego.

4. Wyznaczanie masowej gęstości zasobu energii wewnętrznej gazu doskonałego.

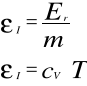
5. Wyznaczanie objętościowej gęstości zasobu energii wewnętrznej gazu doskonałego.

Uwzględniając równanie Haygensa oraz definicje wykładnika izontropy otrzymamy:

Zaś z równania gazu doskonałego Clapeyrona mamy:

Uwzględniając zależność określająca masową gęstość zasobu energii wewnętrznej i dwa ostatnie związki możemy napisać, iż:

Z definicji objętościowej gęstości zasobu energii wynika:

6. Wyznaczenie bilansu zasobu energii wewnętrznej dla układu otwartego w przemianie izobarycznej-izochorycznej.

V=const dV=0

δQ_pr=0

p=const

dE_I=0

0=δQ+hdm

δQ=-hdm

7. Określam masową gęstość zasobu entalpii.

h=c_p⋅τ

8. Wyznaczenie elementu przyrostu masy powietrza dla przemiany izobrycznej-izochorycznej.

9. Wyznaczenie przyrostu ilości ciepła dostarczonego do zbiornika w przemianie izobarycznej-izochorycznej.

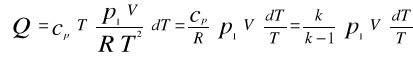
Całkując ostatnią zależność w granicach otrzymamy:

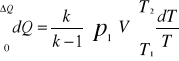
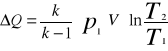
10. Obliczam wartość przyrostu ilości ciepła dostarczonego do zbiornika.

---