Równanie prostej
Wyznaczenie prostej na płaszczyźnie Oxy sprowadza się do wskazania punktu, przez który prosta ma przechodzić i kierunku prostej.
Równanie kierunkowe prostej
Prosta pionowa tzn. równoległa do osi OY ma równanie postaci x = c. (Nie jest to funkcja).
Każda inna prosta ma równanie postaci l: y = ax +b, gdzie a nazywamy współczynnikiem kierunkowym prostej.
Nie każdą prostą można opisać równaniem kierunkowym (np. prostych |
Zależność współczynnika kierunkowego od położenia prostej
Trzy proste przedstawiające funkcję liniową:
(Funkcja - relacja, która każdemu elementowi zbioru X przyporządkowuje dokładnie jeden element zbioru Y.)
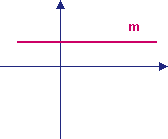
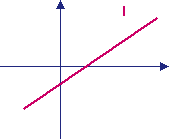
a > 0 a = 0
l: y = ax + b m: y = b
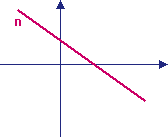
a < 0
n: y = ax + b
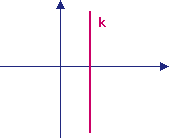
Prosta, która nie jest funkcję liniową:
k: x = c
Dla dowolnej prostej w układzie współrzędnych można dobrać trzy liczby A, B, C, gdzie przynajmniej jedna z liczb A lub B jest różna od zera, takie, że współrzędne każdego punktu tej prostej spełniają równanie Ax + By + C = 0. To równanie nazywamy równaniem ogólnym prostej
l: Ax+By+C=0 gdzie A,B,C to współczynniki liczbowe prostej.
A² + B² > 0 A, B, C
R
Każdą prostą można opisać równaniem ogólnym. |
Mając dane równanie prostej w postaci ogólnej, możemy w prosty sposób przekształcić je do postaci kierunkowej i odwrotnie.
Przykład 1
a) Zapisz podane równania w postaci kierunkowej:
2x - y + 3 = 0
x + 3y -1 = 0
2x + y = 0.
b) Zapisz podane równania w postaci ogólnej:
y =
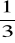
x + 4y = -5
2y + 3x = 2(y - x)
Rozwiązanie
a) Przekształcamy równania w taki sposób, by po jednej stronie równania był sam y, a po drugiej wszystko inne
-y = -2x - 3 /(-1)
y = 2x + 3
3y = -x +1 /:3
y = -![]()
x + ![]()
y = -2x
b) Przekształcamy równania w taki sposób, by wszystkie wyrazy znalazły się po jednej stronie równania
A) ![]()
x - y + 4 =0
y + 5 = 0
2y + 3x = 2y - 2x
2y + 3x - 2y + 2x =0
x = 0
Przykład 2
Podaj wzór takiej funkcji liniowej, która spełnia następujące warunki:
funkcja jest rosnąca, a jej wykres przecina oś y w punkcie (0,-3),
funkcja jest malejąca i jej wykres przecina oś y w punkcie (0,
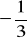
),funkcja jest stała i do jej wykresu należy punkt (10,-20).
Rozwiązanie
Szukamy funkcji y = ax + b.
Jeżeli funkcja jest rosnąca, to jej współczynnik kierunkowy jest liczbą dodatnią (a>0). Ponieważ wykres funkcji przecina oś y w punkcie o współrzędnych (0,-3), więc współczynnik b = -3 i współrzędne tego punktu spełniają równanie szukanej prostej. Stąd otrzymujemy
-3 = a⋅0 + (-3)
Z powyższego równania wynika, że współczynnik a może być każdą liczba rzeczywistą dodatnią , np. dla a=2 równanie przyjmuje postać y = 2x -3.
b) Jeżeli funkcja jest malejąca, to jej współczynnik kierunkowy jest liczbą ujemną (a<0). Ponieważ wykres funkcji przecina oś y w punkcie o współrzędnych (0,![]()
),więc współczynnik b = ![]()
i współrzędne tego punktu spełniają równanie szukanej prostej. Stąd otrzymujemy
![]()
= a⋅0 + (![]()
)
Z powyższego równania wynika, że współczynnik a może być każdą liczba rzeczywistą ujemną , np. dla a= -2 równanie przyjmuje postać y = -2x ![]()
.
Jeżeli funkcja jest stała, to znaczy, że dla każdej wartości argumentu x wartość funkcji jest taka sama, a jej współczynnik kierunkowy jest równy zero. Ponieważ funkcja przechodzi przez punkt o współrzędnych (10,-20), więc szukana funkcja ma wzór y = -20.
Dwie proste są równoległe jeśli leżą na jednej płaszczyźnie i nie mają żadnego punktu wspólnego lub się pokrywają.
Dwie proste są równoległe, gdy:
a) y=a1x+b1|| y=a2x+b2 ![]()
a1=a2 (ich współczynniki są równe)
b) a1x+b1y+c1=0 || a2x+b2y+c2=0 ![]()
a1b1-a2b2=0 ( a1b2=a2b1)
Przykład 3
Znajdź wzór funkcji liniowej, której wykres jest równoległy do wykresu funkcji y = 7x + ![]()
i przechodzi przez punkt (1, 3).
Rozwiązanie
Aby wykresy funkcji liniowych były równoległe ich współczynniki kierunkowe muszą być takie same. Znając współczynnik kierunkowy prostej i współrzędne choć jednego punktu możemy wyznaczyć równanie prostej równoległej do danej i przechodzącej przez podany punkt.
Nasza funkcja ma równanie y = 7x + ![]()
. Jej współczynnik kierunkowy jest równy a = 7, więc współczynnik kierunkowy prostej równoległej do naszej funkcji musi być identyczny. Przyjmując, że szukany wzór ma postać
y = ax + b,
po podstawieniu wartości współczynnika kierunkowego otrzymujemy
y = 7x + b.
Ponieważ szukana prosta ma przechodzić przez punkt o współrzędnych (1,3), więc te współrzędne spełniają jej równanie. Fakt ten wykorzystujemy do wyznaczenia współczynnika b. Podstawiając odpowiednio współrzędne danego punktu do równania szukanej prostej otrzymamy
3 = 7⋅1 + b
b = 3 - 7
b = -4
Zatem prosta równoległa do prostej y = 7x + ![]()
i przechodząca przez punkt (1,3) ma równanie y = 7x - 4.
Przykład 4
Wyznacz współrzędne punktu przecięcia wykresów funkcji f : x ![]()
i g : x![]()
.
Rozwiązanie
Aby wyznaczyć współrzędne punktu przecięcia wykresów dwóch funkcji wystarczy z ich równań zbudować układ i go rozwiązać.
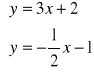
3x + 2 = ![]()
3x + ![]()
= -2 -1
![]()
/![]()
x = -![]()
Mając wyznaczony x podstawiamy go do jednego z równań i wyznaczamy y
![]()
y = 3⋅(-![]()
) + 2
y = -![]()
+ 2
y = -![]()
Zatem wykresy funkcji f i g przecinają się w punkcie o współrzędnych (-![]()
,-![]()
).
Przykład 5
Znajdź wzór funkcji liniowej, której wykres przechodzi przez punkty o współrzędnych (2,1) i (-2,-3).
Rozwiązanie
Szukane równanie możemy zapisać w postaci y = ax + b. Współrzędne danych punktów spełniają to równanie, zatem
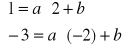
Do rozwiązania tego układu można zastosować metodę przeciwnych współczynników, gdyż przy niewiadomej a mamy liczby przeciwnych znaków.
1 - 3 = 2a - 2a + b + b
-2 = 2b /: 2
b = -1
Podstawiając do pierwszego równania wyznaczoną wartość otrzymamy
1 = 2a -1
1+ 1 = 2a /:2
a = 1
Zatem szukana prosta ma równanie y = x - 1.
Dwie proste są prostopadłe, gdy:
y = a1x + b1 ⊥ y = a2x + b2 ⇔ a1*a2 = -1
a1x+b1y+c1=0 ⊥ a2x+b2y+c2=0 ⇔ a1a2+b1b2=0 ( a1a2=-b1b2)
Przykład 6
Znajdź równanie prostej prostopadłej do prostej y = 8x + ![]()
i przechodzącej przez punkt P= (4, -3).
Rozwiązanie
Szukana prosta ma być prostopadłą do danej, więc jej współczynnik kierunkowy wyznaczamy korzystając z warunku na prostopadłość prostych
y = a1x + b1 ⊥ y = a2x + b2 ⇔ a1*a2 = -1
a1 = 8, więc 8*a2 = -1. Stąd a2 = -![]()
.
Zatem równanie szukanej prostej ma postać y = -![]()
x + b. Aby wyznaczyć współczynnik b, wystarczy rozwiązać równanie -3 = -![]()
⋅ 4 + b.
b = -3 + ![]()
b = -2![]()
Szukana prosta to y = -![]()
x - 2![]()
.
Ćwiczenie 1
Rozwiąż zadania:1, 2 str. 145, 3 -9 str.146, 13, 18 str. 147 z podręcznika.
Wyszukiwarka
Podobne podstrony:
matematyka, Równanie prostej3, Równanie prostej
matematyka, File193, Równanie prostej
matematyka, File193, Równanie prostej
matematyka, File192, Równanie prostej
matematyka, Nierówność prostej3, Równanie prostej
matematyka, Równanie prostej, Równanie prostej
matematyka, Równanie prostej1, Równanie prostej
Rownania rozniczkowe I, Matematyka I+II, Matma I, Matematyka
Układy równań liniowych, Matematyka dla ekonomistów
rownania wielomianowe, Matematyka
równania kwadratowe, Matematyka
Rownania wymierne, Matematyka, Matematyka(4)
Oblicz pole obszaru zawartego między liniami o równaniach y, STUDIA - matematyka
Funkcje Trygonometryczne równania i nierównosci, Matematyka- zadania
Praca klasowa równania i nierówności, Matematyka dla Szkoły Podstawowej, Gimnazjum
równania kwadratowe, Matematyka, Liceum
więcej podobnych podstron