Matematyka na studiach eksternistycznych wspomaganych satelitarnie w roku akademickim 2005/2006

Repetytorium: istotne tematy - internet

1. Elementy topologiczne w Rⁿ: punkt skupienia zbioru, punkt izolowany zbioru, zbiór otwarty, zbiór domknięty, zbiór ograniczony.

2. Nieskończony ciąg liczbowy rzeczywisty: zbieżność, rozbieżność, rozbieżność
   do + ∞, rozbieżność do - ∞. Badanie zbieżności za pomocą podciągów o wskaźnikach parzystych, nieparzystych: przykład a)

a_n =

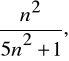
n∈N;

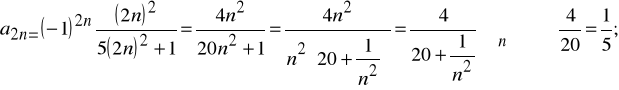
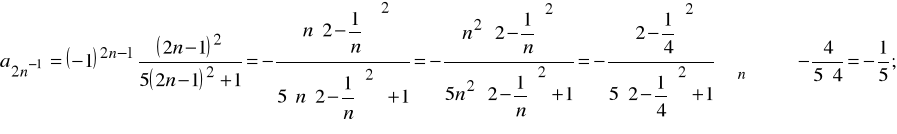
stąd (O_n) _n∈N rozbieżny; przykład b)

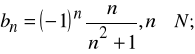
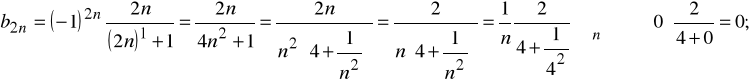
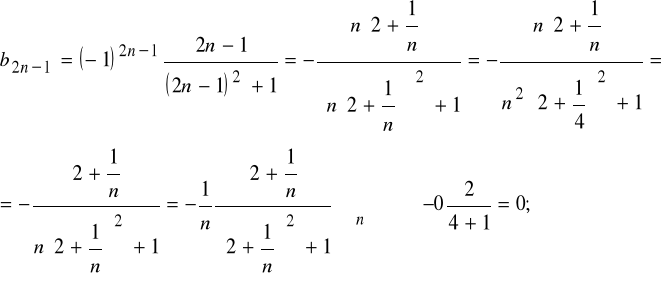
stąd

3. Funkcja rzeczywista 1 zmiennej rzeczywistej: granica funkcji w punkcie, granice jednostronne i ich relacja z granicą, ciągłość funkcji w punkcie i w zbiorze, twierdzenia o funkcjach ciągłych; przykład badania ciągłości funkcji

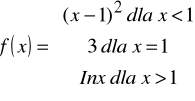
Spr., że x = 1 jest punktem skupienia D_f = R; lim f_(x) = f₍₁₎?

x→1

lim f_(x) = lim (x-1)² = 0 i lim f_(x) = lim Inx = ln 1 = 0, to

x→1 x→1- x→1+ x→1

lim f_(x) = 0; f₍₁₎ = 3, więc f nie jest ciągła w punkcie x = 1;

Interprelacja geometryczna pochodnej funkcji w punkcie; przykład obliczania współczynnika kierunkowego stycznej: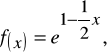
to współczynnik kierunkowy stycznej do wykresu funkcji f w punkcie o odciętej 2 wynosi f '(2), ale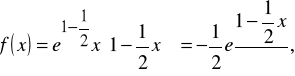
więc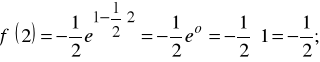
relacja między różniczkowalnością i ciągłością; obliczanie pochodnych ze wzorów, w szczególności ze wzoru na pochodną funkcji złożonej, np.:

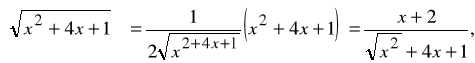
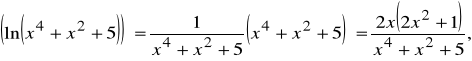
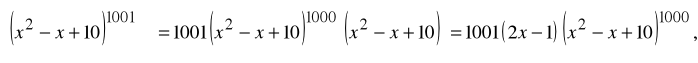
warunki dostateczne monotoniczności, wypukłości, wklęsłości i przykłady że to nie są warunki konieczne; warunek konieczny a) ekstremum, b) punktu przegięcia; warunek dostateczny a) ekstremum, b) punktu przegięcia; ekstrem globalne (twierdzenie Weierstrassa); zastosowanie pochodnych w ekonomii: a) interpretacja ekonomiczna pochodnej rzędu 1-go, b) elastyczność i jej interpretacja, c) tempo zmian funkcji.

4. Funkcja rzeczywista 2 zmiennych rzeczywistych: dziedzina, warstwica; pochodu cząstkowe rzędu 1-go, 2-go; kierunek najszybszego wzrostu, spadku funkcji, gradient funkcji i jego interpretacja, wektor przeciwny do gradientu funkcji i jego interpretacja; monotoniczność względem jednej zmiennej; macierz Hesse, hesjan, pochodne mieszane rzędu 2-go i warunek dostateczny ich równości; warunki ekstremum a) konieczne, b) dostateczne; ekstrema globalne (twierdzenie Weierstrassa); zastosowania ekonomiczne pochodnych cząstkowych: a) interpretacja ekonomiczna pochodnych cząstkowych rzędu 1-go, elastyczności cząstkowe i ich interpretacja, tempo zmian funkcji względem jednej zmiennej, krańcowa stopa substytucji.

5. Algebra liniowa: działania na macierzach i ich własności a) mnożenie, b) transponowanie, c) odwracanie; transpozycja iloczynu, odwracanie iloczynu; macierz symetryczna, warunek konieczny i dostateczny symetryczności, macierze Grama; macierz nieosobliwa, osobliwa, obliczanie wyznacznika metodą rozwinięcia Laplace'a; własności wyznacznika, w szczególności wyznacznik iloczynu macierzy; wyznaczanie macierzy odwrotnej metodą a) dopełnień algebraicznych, b) operacji elementarnych; rząd macierzy i metoda operacji elementarnych jego wyznaczania; macierze równoważne, postać bazowa macierzy; klasyfikacja układów równań liniowych ze względu na a) ilość rozwiązań, b) wektor wyrazów wolnych; warunki konieczne i dostateczne a) niesprzeczności, b) sprzeczności, c) oznaczoności, d) nieoznaczoności wyrażone w terminach rzędów macierzy układu i macierzy rozszerzonej układu; metoda operacji elementarnych rozwiązywania układów równań liniowych, rozwiązania bazowe; układ Cramera i jego rozwiązywanie metodą a) wzorów Cramera, b) macierzy odwrotnej, c) operacji elementarnych; jednorodny układ Cramera i istnienie jego rozwiązań niezerowych; istnienie niezerowych rozwiązań jednorodnych układów równań liniowych.

1

1

---