Korzonkiewicz Paweł Wydział Fizyki Technicznej

Juraszek Gabriel Informatyki i Matematyki

Grupa w 209 Stosowanej

Informatyka

Ćwiczenie nr 56

Temat: badanie wpływu temperatury na przewodnictwo elektryczne przewodników i półprzewodników

I. Część teoretyczna.

1.Model pasmowy, przewodnictwo elektryczne przewodników i półprzewodników, półprzewodniki samoistne i domieszkowe.

Zgodnie z teorią mechaniki kwantowej atom może znajdować się w określonych stanach energetycznych. Oznacza to, że orbitom, po których może poruszać się elektron odpowiadają poziomy energetyczne. Jeżeli od pojedynczego atomu przejść do ciała stałego o budowie krystalicznej to, ponieważ kryształ składa się z bardzo wielu blisko siebie ułożonych i tworzących tzw. siatkę krystaliczną atomów, poziomy energetyczne ulegają rozszczepieniu w tzw. pasma.

Pasmo jest to zbiór poziomów energetycznych elektronów wszystkich atomów znajdujących się w danej objętości kryształu.

Ze względu na właściwości elektryczne materiały stosowane w elektronice dzieli się na:

1. Przewodniki

2. Izolatory

3. Półprzewodniki

Energetyczne modele pasmowe:

W W W

Pasmo przewodnictwa Pasmo przewodnictwa Pasmo przewodnictwa

Wg ˜10 eV Wg < 2eV

Pasmo podstawowe Pasmo podstawowe Pasmo podstawowe

X X X

Szerokość pasma zabronionego Wg określa się ilością energii (w elektronowoltach), jaką elektron musi uzyskać do “przeskoczenia” tego pasma i przejścia z pasma podstawowego (walencyjnego) do pasma przewodnictwa.

Przewodnik charakteryzuje się tym, że najwyższe pasmo energetyczne zawierające elektronu walencyjne nie jest całkowicie obsadzone. Wobec gęstego rozmieszczenia dozwolonych poziomów energetycznych w tym paśmie małe ilości dostarczanej energii wystarczają do przeniesienia elektronu na wyższy poziom energetyczny w obrębie tego samego pasma. Energii tej może dostarczyć np. słabe pole elektryczne.

W izolatorach najwyższe pasmo energetyczne zawierające elektrony jest całkowicie zapełnione i oddzielone jest od pasma przewodnictwa przerwą energetyczną Wg. Przerwa ta jest tak duża, że ani stosunkowo dość silne pole elektryczne, ani ogrzanie nie wystarczają do przeniesienia elektronu do wyższego pasma dozwolonego.

Półprzewodniki podobnie jak w przypadku izolatorów najwyższe pasmo energetyczne zawierające elektrony, tzw. Pasmo walencyjne, jest całkowicie zapełnione, ale przerwa między pasmem przewodnictwa jest mniejsza, co pozwala na przejście elektronu do tego pasma dzięki np. temperaturze.

Półprzewodniki dzieli się na:

1. Samoistne

2. Domieszkowe

Półprzewodnik samoistny jest to czysty chemicznie kryształ bez żadnych domieszek (np. krzem, german), który w temperaturze zera bezwzględnego nie przewodzi. Wzbudzenie elektronów np. temperaturą jest równoznaczne z pojawieniem się dwóch nośników ładunku elektrycznego swobodnego ujemnego elektronu w paśmie przewodnictwa i dodatniej dziury w paśmie walencyjnym. Po przyłożeniu napięcia prąd płynący przez kryształ jest sumą prądu elektronowego i dziurowego.

Półprzewodniki domieszkowe to takie, które zawierają w węzłach sieci krystalicznej atomy innych pierwiastków (np. german z domieszką arsenu), co ma znaczny wpływ na poprawienie się właściwości elektrycznych półprzewodników.

2.Wpływ temperatury na oporność ciał stałych.

W półprzewodnikach w miarę wzrostu temperatury zwiększa się energia ruchu cieplnego atomów, dzięki czemu w wyniku zderzeń więcej elektronów może uzyskać energię wystarczającą do przejścia z pasma walencyjnego do pasma przewodnictwa. Tym samym ze wzrostem temperatury zwiększa się liczba generowanych par nośników ładunku: elektron-dziura i maleje opór elektryczny półprzewodnika. Zjawisko ma, więc charakter odwrotny niż w przypadku metali, które w tych samych warunkach wykazują wzrost oporu elektrycznego(związane jest to z pojęciem poziomu Fermego).

W temp. zera bezwzględnego elektrony stopniowo zapełniają kolejne poziomy licząc od podstawowego. Po rozmieszczeniu wszystkich elektronów swobodnych jest sytuacja gdzie pewien poziom energetyczny rozgranicza poziomy całkowicie zapełnione od całkowicie pustych. Ten poziom nazywa się “poziomem Fermego”. Pod wpływem temp. tylko nieliczne elektrony, te znajdujące się zaraz pod poziomem Fermego, potrafią przeskoczyć do pasma przewodnictwa i być odpowiedzialne za przewodnictwo cieplne i elektryczne przewodników, (dlatego opór przewodników rośnie ze wzrostem temperatury).

Nadprzewodnictwo jest to zanik oporu elektrycznego przewodników w temperaturach bliskich zera bezwzględnego.

Fermego energia max. Energia elektronów przewodnictwa w metalu w temp. 0[K]

Debye'a prawo w temperaturze bliskich zera bezwzględnego Ciepło właściwe ciał stałych jest proporcjonalne do trzeciej potęgi temperatury bezwzględnej.

II. Część laboratoryjna

Rezystancja przewodników zależy od warunków fizycznych, w jakich znajdują się te przewodniki, a przede wszystkim od temperatury.

opór elektryczny przewodnika w temperaturze otoczenia (20şC)

przyrost temperatury

temperaturowy współczynnik rezystancji (względny przyrost rezystancji przy wzroście temp. o 1 K)

y = b + ax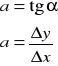

y = b + ax
⇒

E -szerokość pasma zabronionego (
)

K -stała Boltzmanna (
)

b -wyraz stały prostej regresji

a -współczynnika nachylenia prostej regresji

Aa -błąd współczynnika a

Ab -błąd stałej b

R -współczynnik dopasowania do punktów doświadczalnych

Przewodnik: Półprzewodnik:

a =0,003927 a =3942,31

b =0,993287 b =-11,01

Aa =4,11 E^-5 Aa =28,31

Ab =0,002729 Ab = 0,02

R =0,998796 R =1,00

Wyniki pomiarów doświadczenia obliczone na podstawie wyżej wymienionych wzorów:

Przewodnik				Półprzewodnik
T[°C]	ΔT[K]	R[Ω]	R/R	T[K]	1/T[K ]	R[kΩ]	lnR
22.5 25 30 35 40 45 50 55 60 65 70 75 80	0 2,5 5 5 5 5 5 5 5 5 5 5 5	17,88 17,96 18,25 18,59 18,96 19,30 19,66 20,01 20,38 20,74 21,12 21,47 21,84	1 1,01 1,02 1,04 1,06 1,08 1,10 1,12 1,14 1,16 1,18 1,20 1,22	296,5 299 304 309 314 319 324 329 334 339 344 349 354	0,0034 0,0033 0,0033 0,0032 0,0032 0,0031 0,0031 0,0030 0,0030 0,0029 0,0029 0,0028 0,0028	9,92 9,24 7,55 6,01 4,90 3,93 3,23 2,71 2,23 1,89 1,60 1,38 1,19	2,29 2,22 2,02 1,79 1,58 1,37 1,17 1,00 0,80 0,64 0,47 0,32 0,17

Zgodnie z powyższymi wyprowadzeniami szerokość pasma zabronionego dla badanego półprzewodnika wynosi zgodnie ze wzorem:

gdzie:

k - stała Boltzmana

a - współczynnik kierunkowy prostej lnR = f (1/T)

Po podstawieniu otrzymujemy:

E=1,38*10^-23 * 3942,31=5440,39*10^-23 [J]

E=0,34 [eV]

---