Geometria - własności miarowe I
Wyznacz promień okręgu wpisanego w trójkąt równoramienny o podstawie 10 cm i kącie między ramionami
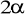
.Oblicz pole trójkąta równobocznego mając daną długość promienia okręgu wpisanego r.
Oblicz pole trójkąta równobocznego mając daną długość promienia okręgu opisanego R.
Obwód rombu jest równy 20, a suma jego przekątnych 14. Obliczyć pole i wysokość rombu.
W trapezie równoramiennym o długościach podstaw 10 oraz 6 kąt rozwarty trapezu ma miarę
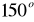
. Obliczyć pole trapezu i długość tworzącej.Podstawą ostrosłupa jest prostokąt o przekątnej długości 6 i kącie
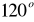
między przekątnymi. Każda z krawędzi bocznych ostrosłupa tworzy z płaszczyzną jego podstawy kąt o mierze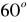
. Oblicz objętość ostrosłupa.W ostrosłupie prawidłowym czworokątnym krawędzie podstawy i krawędzie boczne mają jednakową długość. Oblicz miarę kąta nachylenia krawędzi bocznej do płaszczyzny podstawy.
Dany jest sześcian o krawędzi a. Obliczyć pole powierzchni całkowitej ostrosłupa, którego wierzchołkami są: środek górnej podstawy sześcianu i środki boków dolnej podstawy.
Podstawa graniastosłupa prawidłowego sześciokątnego jest wpisana w koło o promieniu 1. Najdłuższa przekątna graniastosłupa tworzy z płaszczyzną podstawy kąt o mierze
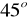
. Oblicz objętość tej bryły.Wysokość czworościanu foremnego ma długość h. Oblicz objętość i pole powierzchni całkowitej tego czworościanu.
Wyszukiwarka
Podobne podstrony:
geometria w płaszczyźnie
GEOMETRIA
GEOMETRIA OBLICZENIOWA I
lec6a Geometric and Brightness Image Interpolation 17
Geometria wykreślna Ćwiczenie 8
Algebra liniowa i geometria kolokwia AGH 2012 13
Geometria wykreślna przenikanie brył2
GK 9 Przekształcenia geometryczne
Zynel M Geometria elementarna id 106714
Kompleksowa rozgrzewka z pilkam Nieznany
Geometria Wykreślna wykłady
Geometria krzywych i powierzchn Nieznany
Geometria W 1 2
Kompleksowa rozgrzewka z pilkam Nieznany (2)
geometria analityczna
Co to jest teoria względności podstawy geometryczne
geometria zadania 1 25 aksonome Nieznany (3)
więcej podobnych podstron