1. Struktura niezawodnościowa z redundancją.
• Struktura obiektu, który jest sprawny gdy co najmniej k dowolnych spośród n jego elementów jest sprawnych, nazywa się strukturą typu k z n co zapisuje się krótko jako k/n i nazywa się strukturą progową.
• Jeśli: k < n to jest to struktura z redundancją (nadmiarowością);
• k = n to jest to struktura szeregowa;
• k = l to jest to struktura równoległa.
2. Uogólnione prawo wzrostu
Co to jest prawo wzrostu ?
Jeżeli ze wzrostem liczby elementów składowych obiektu lub ze wzrostem złożoności analizowanego procesu prawdopodobieństwo uszkodzenia czy niepowodzenia rośnie mówi się o prawie wzrostu prawdopodobieństwa lub w skrócie o prawie wzrostu. Prawo to jest szczególnie użyteczne gdy zachodzi potrzeba wnioskowania o złożonych obiektach w oparciu o wyniki badań ich fragmentów.
![]()
![]()
• Jeśli obiekt lub proces składa się z N oddzielnych elementów o różnych rozkładach Fl(x), F2(x), ... ,FN(x) to wówczas prawo wzrostu przybiera postać będącą odpowiednikiem równania 11.2 dla niezawodności.
To uogólnione prawo wzrostu można stosować dla konstrukcji składających się z wielu różnych elementów np. dla transformatorów, stacji lub linii elektroenergetycznych, złożonych procesów technologicznych itp.
Zastosowanie prawa wzrostu o postaci 12.5 prowadzi do tego, że rozkład F(N,x) jest rozkładem wielomodalnym. Dokładna analiza tego typu rozkładów złożonych jest możliwa jedynie za pomocą komputera
3. Czy możliwe jest uzyskanie niezawodności Rx>Rxmax?
Żądanie aby niezawodność Rx była większa niż niezawodność dyspozycjonalna Rxmax jest niewykonalne dyspozycjonalnie. Możliwość dyspozycjonalna -wykonania żądania istnieje gdy:
- to co jest do zrobienia jest niegrzeczne współcześnie z prawami fizycznymi, fizjologicznymi i w ogóle' z prawami natury i prawami logiki;
- istnieje możliwość zaangażowania w procesie realizacji najdoskonalszych środków technicznych i wykonawców o największych umiejętnościach i rutynie.
Rtmax - maksymalna niezawodność techniczna uzyskiwana lokalnie - określona przez fizyczną niemożliwość przekroczenia jej przy aktualnym stanie wiedzy, umiejętnościach i rutynie uczestników procesu realizacji;
4. Związek między niezawodnością i dystrybuantą ?
F=1-R
5. Do czego służą karty kontrolne ?
Karta kontrolna to formularz, na którym rejestrowane są określone miary statystyczne właściwości wyrobów, uzyskane w wyniku badania próbek pobieranych losowo w określonym miejscu procesu produkcji. Służą one do kontroli procesów produkcji w toku.
6. Do czego służy plan badania ?
Plany badania oparte są o testy istotności polegające na przyjęciu lub odrzuceniu weryfikowanej hipotezy ϑ0. Jest przy tym zapewnione prawdopodobieństwo co najwyżej α popełnienia błędu I rodzaju tzn. odrzucenia hipotezy ϑ = ϑ0 gdy jest ona słuszna (prawdziwa). Jednak hipoteza ϑ = ϑ0 może nie być zakwestionowana również wówczas gdy prawdziwa wartość parametru ϑ różni się od wartości ϑ0. Interesująca jest więc zależność prawdopodobieństwa przyjęcia hipotezy ϑ = ϑ0 od prawdziwej wartości parametru ϑ.
7. Do czego służy system kontowy?
System kontowy służy do kontroli poddostawców. System można stosować do kontroli odbiorczej produktów sztukowych, w przypadku oceny alternatywnej poszczególnych sztuk w próbce.
8. Ryzyko odbiorcy i wytwórcy.
Ryzyko odbiorcy jest to ryzyko przyjęcia partii wadliwej, natomiast ryzyko dostawcy jest to ryzyko odrzucenia partii dobrej.
9. Badanie sekwencyjne.
Procedura planu sekwencyjnego jest następująca:
a) należy pobierać, z kontrolowanej partii produktu, po jednej sztuce i sprawdzać kolejno na zgodność z ustalonymi wymaganiami;
b) po sprawdzeniu każdej sztuki należy obliczyć:
r=(H+i)-b⋅z gdzie:
H i b- parametry planu badań odczytane np. z tablicy 4D;
i- liczba sztuk dobrych po kolejnym stopniu badań
z- liczba sztuk niedobrych po kolejnym stopniu badań
M - maksymalna liczba badanych sztuk.
c) należy uznać partię produktu za zgodną z wymaganiami jeśli r = 2 H;
d) należy uznać partię produktu za niezgodną z wymaganiami gdy r ≤ 0;
e) należy kontynuować badanie jeśli O < r < 2 H;
f) należy zastosować ostatni stopień odpowiedniego wielostopniowego planu badania jeśli łączna liczba zbadanych sztuk osiągnie M.
W planach sekwencyjnych średnia liczność próbki jest najmniejsza ze wszystkich planów badań
Należy je stosować wtedy, gdy ze względów ekonomicznych lub technicznych mała próbka jest
konieczna i gdy wielokrotne pobieranie próbek jednosztukowych nie jest trudne ani kosztowne.
10. Niepewność - oszacowanie funkcji wielu zmiennych.
![]()
Zakładając, że x, ... , z zmierzono z
niepewnościami δx, .... , δz i wartości te służą do obliczenia wartości funkcji q(x,....,z). Jeżeli niepewności wyznaczania x,....,z są niezależne i przypadkowe to niepewność wyznaczenia wartości funkcji q wynosi:
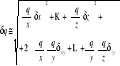
Jeżeli wielkości wejściowe są skorelowane to złożoną niepewność oblicza się ze wzoru: δxy oraz δyz odpowiednie kowariancje
11. Niezawodność obiektu.
Niezawodność obiektu jest to właściwość określona przez wartości istotnych wielkości charakteryzujących zdolność obiektu do spełnienia wymagań.
Wielkością charakteryzującą zdolność do spełnienia wymagań może być prawdopodobieństwo spełnienia przez obiekt stawianych mu wymagań- Czyli niezawodność to prawdopodobieństwo sukcesu. Niezawodność obiektu to prawdopodobieństwo, że wartości parametrów określających istotne właściwości obiektu nie przekroczą w ciągu okresu czasu (O, t) dopuszczalnych granic, w określonych warunkach życia obiektu.
12. Funkcja intensywności uszkodzeń lub ryzyka.
Zależność określającą jaka część obiektów, które przetrwały sprawne w przedziale (O, t) stanie się prawdopodobnie niesprawna w przedziale (t, t + dt) nazywa się funkcją ryzyka albo funkcją intensywności uszkodzeń. Kształt funkcji ryzyka jest istotny przy ocenie właściwości niezawodnościowych obiektu.
13. Karta X-R.
Służy do kontroli zmian właściwości ocenianych liczbowo np. wymiaru, wagi, gęstości,
wytrzymałości, temperatury, czasu przestoju itp.
Kontroluje tylko jedna właściwość.
Jest kartą dwutorową: tor średniej X i tor rozstępu R.
Może zawierać dodatkowe tory np. liczby sztuk niedobrych, grup pozostałych właściwości,
innych pojedynczych właściwości.
dla karty X-R liczność próbki winna mieścić się w granicach 10;
14. Co jest potrzebne do obliczenia ryzyka uszkodzeń ?
Aby obliczyć ryzyko uszkodzeń danego obiektu, trzeba znać jego strukturę oraz niezawodność poszczególnych elementów.
15. Na czym polega sygnał na karcie kontrolnej zwany uwarstwieniem (stabilifron) ?
Uwarstwienie jest czasem określane jako "trzymanie się linii centralnej". Jest to pewna sekwencja punktów na karcie kontrolnej, z których duży procent leży wokół linii centralnej.
16. Plany badań według oceny alternatywnej, który wymaga najmniejszej liczebności próbek.
W planach sekwencyjnych średnia liczność próbki jest najmniejsza ze wszystkich planów badań.
17. Jeżeli znasz ryzyko uszkodzenia obiektu R=0.1, to ile wynosi niezawodność obiektu.
Niezawodność wynosi l-R czyli 0.9.
18. Co to jest trwałość obiektu ?
Trwałość jest jedną z podstawowych cech wszystkich obiektów technicznych. Jest to zdolność obiektu do zachowania posiadanych właściwości. Miarą trwałości obiektu jest najczęściej czas, w ciągu którego zachowuje on posiadane właściwości. Niekiedy trwałość obiektu wyraża się również ilością wykonanej pracy, liczbą wykonanych czynności (np. liczbą łączeń dla łączników elektroenergetycznych lub liczbą lądowań w przypadku samolotu), długością przebytej drogi (pojazdy) itp. Trwałość obiektu technicznego jest więc - w odróżnieniu od jego niezawodności -wielkością mianowaną, wyrażoną w jednostkach czasu, długości, liczby łączeń, wielkości urobku itp.
Ten sam obiekt techniczny może być wykonany w taki sposób, że będzie miał różną trwałość. Właściwość ta ma charakter jakościowy. Zwykle obiekty techniczne o większej trwałości uznaje się za lepsze.
19. Fenomen FREAK PATERN.
Jest to sygnał polegający na sekwencji punktów na karcie kontrolnej, dla których występuje pewien duży procentowy spadek poniżej linii centralnej. Przykładowe kryteria dla tego sygnału mogą być następujące: (a) 2 spośród 3 punktów są poza granicą kontrolną zewnętrzną (2σ) lub (b) 4 spośród 5 punktów są poza granicą kontrolną wewnętrzną (lσ).
Fenomen może być traktowany jako sygnał rozregulowania się badanego procesu gdyż: (l) tylko nieliczne punkty - dla jedynie losowych zmian - mogą wychodzić poza linie ostrzegawcze; (2) jeśli proces jest ustabilizowany to mniej niż 5% punktów może wychodzić poza 2σ (ostrzeżenie) i mniej niż 32% punktów może wypaść poza 1σ (ostrzeżenie).
Przyczyny fenomenu mogą być następujące: drastyczna zmiana surowca, pominięcie jakiejś operacji w procesie technologicznym, niewykonanie jakiejś operacji w całości rtp.
Fenomen może świadczyć również o jakimś większym zjawisku
20. Który zapis jest poprawny: 9.0110.4; 9.01±0.04; 9.01±0.0004.
21. Podaj wzór na niepewność wartości dowolnej funkcji jednej zmiennej.
Jeśli x jest mierzone z niepewnością 5x i wykorzystywane do obliczenia wartości funkcji q(x) to niepewność δq jest równa:
22. Test Hartleya
Warunki i procedura stosowania testu:
![]()
próbki mają jednakową liczność n = const;
należy obliczyć wariancję maksymalną S2max oraz minimalną S2min ;
wartość testowa wynosi: Ft = (S2 max) / S2 min
jeżeli wartość testowa ft <ft gdzie t jest wartością krytyczną testu, to na poziomie istotności a hipotezy zerowej o równości wariancji odrzucić nie można. Wartości y; podano w tabeli 14.5 dla k = 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 (poziomo) oraz n = 2,3, 4, 5, 6, 7, 8, 9, 10, 12, 15, 20. 30, 60, ∞ (pionowo).
![]()
![]()
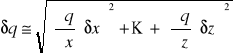
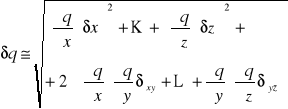
![]()
Wyszukiwarka
Podobne podstrony:
Algebra zbiorów, Ściągi dla studentów, Matematyka
zagadnienia matematyczne, Ściągi dla studentów, Matematyka
Matematyka - wzory, Ściągi dla studentów, Matematyka
Matematyka finansowa - wzory, Ściągi dla studentów, Matematyka
Postac iloczynowa trojmianu kwadratowego, Ściągi dla studentów, Matematyka
matematyka finansowa, Ściągi dla studentów, Matematyka
Matematyka - aproksymacja i interpolacja, Ściągi dla studentów, Matematyka
Ulamki egipskie, Ściągi dla studentów, Matematyka
analiza rentownosci, Ściągi dla studentów, Matematyka
Fraktale, Ściągi dla studentów, Matematyka
ciagi szeregi, Ściągi dla studentów, Matematyka
Algebra zbiorów, Ściągi dla studentów, Matematyka
pedagogika czasu wolnego - bielecka, Nauka, ściagi dla studentów turystyki i rekreacji ;)
więcej podobnych podstron