Def. Ciąg funkcyjny:
Ciąg funkcyjny w zbiorze A jest to przyporządkowanie każdej liczbie naturalnej dokł. jednej określonej na tym zbiorze. Funkcję przyporządkowaną liczbie naturalnej n ozn. fn(x) natomiast cały ciąg będziemy oznaczać {fn (x) } który po napisaniu daje: (f1 (x) i f2 (x), ...). Jeżeli ciąg funkcyjny {fn(x)}jest określony w A, to dla każdego x0∈A do funkcji granicznej z ciągu funkcyjnego, otrzymamy konkretny ciąg liczbowy {fn(x0)}, który jest zbieżny lub rozbieżny.
Def. Zbieżność ciągu funkcyjnego do funkcji granicznej:
Ciąg funkcyjny {fn(x)} jest zbieżny w A do funkcji granicznej f(x), co zapisujemy limn→∞fn(x)-f(x) lub fn(x) ne→∞→ f(x) ⇔ Λε>0 Λx∈Α Vs Λn>s. fn(x)- f(x)<ε oprócz zbieżności ciągu funkc. mówimy o jego zbieżności jednostronnej, którą ozn. symbolem: Λfn(x) A⇒f(x) ⇔ Λε>0 Vδ Λx∈A fn(x)- f(x)<ε
Dla zb. zwykłej liczba δ ma istnieć dla każdego ε>0 i x∈A
Dla zb. jednostronnej ma mieć jednakową wartość dla całego zbioru A
Ze zbieżności jednostronnej wynika zbieżność zwykła
[fn(x) A⇒ f(x)] ⇒ [fn(x) e→ f(x)]
Tw. Granica jednostajnie zb. ciągu f. ciągłych jest f. ciągłą
Warunek Cauche'go:
Na to aby ciąg fn(x) był zbieżny jednostajnie w zbiorze A potrzeba i wystarcza aby Λε>0 Vr że Λn>r zachodzi [fn(x) - fr(x)]<ε
-Szereg geometryczny:
Saqn-1 lub Saqk
1. Jeżeli a=0 to szer. zb. & S= 0
2. Jeżeli a≠0 to szer. geom.
-dla q<1 szer. geom. zb. i S=a/1-q
-dla q≥1 szer. geom. rozb.
-Szereg Dirchleta: S1/na , a∈R, dla α>1 sz zbieżny; dla a ≤1 sz rozbieżny.
-Szereg naprzemienny: Szereg Σ(-1)n+1an, gdzie an>0 dla n=1,2,3,… nazywamy szer naprzemiennym.
Def. Zbieżność szeregu liczbowego:
Szereg liczbowy nazywamy zbieżnym, jeżeli ciąg sum częściowych jest zbieżny do granicy właściwej lim Sn =S ; S- suma szeregu.
Def. Równość szeregów:![]()
Z równości szeregów wynika równość ich sum, ale nie na odwrót.
Def. Iloczyn przez liczbę:![]()
Def. N- reszta szeregu: jeżeli w szeregu Σak pominiemy n początkowych wyrazów to otrzymamy szereg: ![]()
który nazywamy n - resztą szeregu Σak .
Tw. Jeżeli szeregi Σan; Σbn są zbieżne, a ich sumy wynoszą odpowiednio: S1 i S2 to Σ(an+ bn ) i Σ(kan) wynoszą odpowiednio S1+S2 i kS1 .
Tw Warunek konieczny zbieżności szeregu:
Jeżeli szereg Σan jest zbieżny, to lim an=0
Dowód:
an=Sn-Sn-1 ; lim an= lim (Sn-Sn-1) = lim Sn - lim Sn-1 = S-S=0
Tw. Zbieżność szeregu: Jeżeli ciąg sum częściowych szeregu o wyrazach nieujemnych jest ograniczony z góry, to szereg ten jest zbieżny.
Dowód:
Sn=a1+ a2+ a3+…+ an Λ an≥0, ciąg Sn jest ciągiem niemalejącym, ciąg ograniczony z góry z założenia. Każdy ciąg monotoniczny i ograniczony jest zbieżny ⇒ Sn -jest zbieżny.
Kryterium porównawcze:
Jeżeli wyrazy szeregów Σ an i Σ bn są nieujemne, a ponadto istnieje taka liczba naturalna n0 , że n> n0 i spełniona jest nierówność an≤ bn, to:
- ze zbieżności szer bn wynika zbieżność szeregu an
- z rozbieżności szeregu an wynika rozb szeregu bn
Dowód:
Sn=Σ an - chcemy pokazać, że jest zbieżny.
Sn = Sn0+Σak ≤ Sn0 +Σbk ≤ Sn0 + B;
k= n0 +1 ciąg sum częściowych Sn =Sn0 + B jest ograniczony stąd wynika zbieżność Σbk\n z założenia zbieżny i równy B.
Kryterium d'Alamberta:
Jeżeli istnieje granica właściwa lub niewłaściwa g=lim an+1/an, to szereg Σan o wyrazach dodatnich jest zbieżny, gdy g<1, natomiast rozb dla g>1.
Kryterium Cauchyego:
Jeżeli istnieje granica właściwa lub niewłaściwa g=lim n√an, to szereg o wyrazach nieujemnych jest zbieżny gdy g<1, natomiast rozb dla g>1.
Kryterium całkowe:
Niech funkcja f(x) będzie funkcją ciągłą, malejącą i dodatnią dla x≥ n0∈N wówczas war koniecznym i dostatecznym zbieżności takiego szeregu jest zbieżność całki n0∫∞ f(x)dx
Kryterium Leibniza:
Jeżeli ciąg {an} jest nierosnący oraz lim an=0, to szereg naprzemienny jest zbieżny.
[Ciąg nierosnący Λan+1≤an ]
Kryterium Weierstrassa:
Jeżeli Σan liczb. jest zbież i jeżeli![]()
spełniona jest nierówność fn(x)≤an to Σ funkcyjny jest zbieżny jednostajnie i bezwzględnie w zbiorze A. Σan nazywamy majorantą Σ funkcyjnego.
Dowód:
Σan jako zbieżny musi spełniać warunek:
![]()
![]()
![]()
![]()
- war. konieczny i dostateczny zb Σ funkcyjnego.
Def: Bezwzględna zbieżność szeregu:
Σan nazywamy bezwzględnie zbieżnym jeżeli jest zbieżny Σ złożony z bezwzględnych wartości. Jeżeli Σan jest zbieżny bezwzględnie, to jest zbieżny. (Σan )=Σ (an). Jeżeli Σ jest zbieżny to nazywamy go warunkowo zbieżnym.
Def. Iloczyn Caychy'ego szeregów:
Szereg Σan, gdzie an = Σ ak bn-k+1; n=1,2...- nazywamy iloczynem Cauchy'ego szeregów Σan i Σbn tzn:
(Σan ) (Σbn ) = Σan
(Σan ) (Σbn ) = Σan ak =Σak bn - k
Twierdzenie: Jeżeli szeregi Σan i Σbn s --> [Author:AS] ą zbieżne i chociaż jeden z nich jest bezwzględnie zbieżny, to ich iloczyn jest zbieżny.
Tw. Całkowanie szeregu funkcyjnego:
Jeżeli Σfn(x) o wyrazach ciągłych w przedziale <a,b> jest w tym przedziale jednostajnie zbieżny to 0∫b[Σfn(x)]dx=Σ0∫bfn(x)dx.
Tw. Różniczkowanie szeregu funkcyjnego:
Jeżeli wyrazy sz. Funkcyjnego mają ciągłe pochodne f'n(x) w przedziale <a,b>, Σ funkcyjny Σfn(x) jest zbieżny w przedziale <a,b> a ponadto sz.Σf'n(x) jest jednostajnie zbieżny w przedziale <a,b> to:
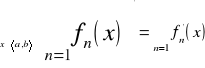
Def. Promień szeregu potęgowego:
Promieniem R zbieżności Σ potęgowego Σanxn nazywamy kres górny zbioru bezwzględnych wartości x dla Σ ten jest Σ zbieżnym.
Tw. Promień szeregu potęgowego:
Jeżeli istnieje granica:
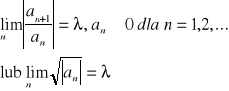
to promień zbieżności szeregu Σanxn wynosi:
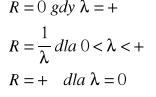
Tw. Całkowanie szeregu potęgowego:
Jeżeli x należy do wnętrza przedziału Σ pot. Σ anxn tzn. x∈(-R,R) to całka: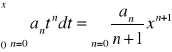
przy czym promień zbieżności tego szeregu jest taki jak szeregu wyjściowego.
Dowód: Założenia o całkowaniu szeregu są spełnione dla: 
Tw. Różniczkowanie szeregu potęgowego:
Jeżeli x należy do wnętrza przedziału zb. Σ pot. Σ anxn to pochodna: ![]()
- promień zb. tego Σ jest taki sam jak szeregu wyjściowego.
Uzasadnienie: zał. Tw. o różniczkowaniu Σ funkcyjnego są spełnione czyli możemy różniczkować wyraz po wyrazie:
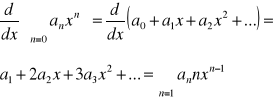
Szereg Taylora:
Niech f będzie funkcją, która ma w pewnym otoczeniu Q punktu x0 wszystkie pochodne, tzn. jest klasy C∞. Funkcję taką dla każdego x∈Q-{x0} i każdego n∈N możemy rozwinąć w Σ Taylora:
![]()
Tw. o reszcie Taylora:
Jeżeli istnieje liczba M.>0, że![]()
Spełniona jest nierówność:
![]()
czyli funkcja daje się rozwinąć w otoczeniu Q w Σ Taylora.
Dowód:
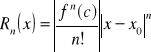
szacujemy moduł z reszty.
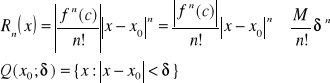
badamy zbieżność Σ z d'Alamberta:
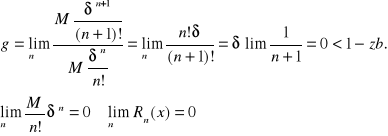
Rozwinięcie w szereg Taylora:
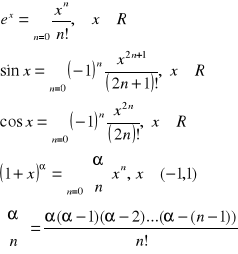
Szereg Fouriera:
Jeżeli dana jest funkcja f:<a,a+2l>→R, to szereg trygonometryczny
![]()
gdzie:
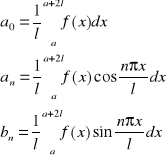
nazywamy trygonometrycznym szeregiem Fouriera funkcji f(x) i będziemy zapisywali:
![]()
,
Warunki Dirchleta:
Mówimy że funkcja f:<a,a+2l)→R ograniczona spełnia w przedziale <a;a+2l>Warunki Dirchleta jeżeli a) funkcja ta jest przedziałem monotoniczna: b) funkcja fest cuągła za wyjątkiem co najwyżej skończonej liczby punktów w których ma nieciągłość pierwszego rodzaju
Nieciągłość usuwalna Nieciągłość nieusuwalna
Lim f(x)= lim f(x)≠f(x0) Lim f(x)= lim f(x)
Χ→X0- Χ→X0+ Χ→X0- Χ→X0+
Twierdzenie: Trygonometryczny szereg Fouriera dla funkcji f. która działa w przedziale f;<a;a+2l>→R spełniająca warunki Dirchleta, jest zbieżny w każdym punkcie przedziału <a; a+2l> przy czym w dowolnym punkcie x0∈(a;a+2l) w którym f. f: fest ciągła suma szeregu wynosi f(x) natomiast w punktach x0∈(a;a+2l) w któryvh funkcja f jest nieciągła suma szeregu wynosi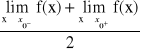
-śr. arytmet. granic jednostronnych
Na krańcach przedziału suma szer. wynosi 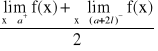
Macierze:
Def. Podobieństwo Macierzy:
Macierz kwadratową A nazywamy podobną do macierzy kw. B, jeżeli istnieje nieosobliwa macierz P (det≠0) taka, że B=P-1AP, macierz P. nazywamy macierzą podobieństwa
Tw: Jeżeli macierz A jest podobna do macierzy b z macierzą podobieństwa P., to macierz B jest również podobna do macierzy A z macierzą podobieństwa P-1
Dowód: B=P-1AP *P.
PB=AP ⇒ PB*P-1=A
Def. Macierz ortogonalna:
Macierz kwadratową i nieosobliwą A nazywamy ortogonalną ⇔
1. detA=±1
2. A*AT =E
Dowód:
A - ortogonalna:
AAT=E, AA-1=E
AAT=AA-1|*A-1
A-1AAT= A-1AA-1⇒ EAT= EA-1⇒ AT= A-1
Definicja Bazy:
Układ B{e1,e2} gdzie ![]()
są wektorami liniowo niezależnymi nazywamy bazą w przestrzeni V2 (analogicznie dla B-{e1,e2,e3} (Trzy wektory ![]()
liniowo niezależne jeżeli kombinacja ![]()
Bazę B nazywamy ortonormalną gdy wszystkie wektory bazowe mają dł. równą 1 i są wzajemnie do siebie prostopadłe
Macierz przejścia:
Dane są dwie bazy: B{e1,e2, e3} oraz B'{e1',e2', e3'} w prz.V3. Z definicji bazy:
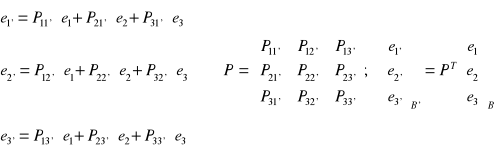
Tw. Macierz przejścia P od bazy ortonormalnej B do bazy B' jest zawsze macierzą ortogonalną: PT=P-1
Zmiana współrzędnych wektora przy zmianie bazy:
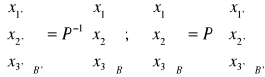
Def: Operacji liniowej:
Operacja A: V3→V3 (A: V2→V2) nazywamy liniową jeśli spełnia warunek:
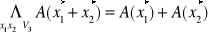
- warunek addytywności (analogiczności dla V2)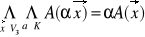
-w jednorodności
Def: Operacji jednostkowej:
Operację A, która działa w V3→V3 (lub A: V2→V2 ) nazywamy jednostkową jeżeli: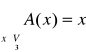
A=E - ozn. op. jednostkowej.
Macierz operacji jednostkowej:
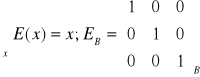
Macierz operacji jednostkowej nie zależy od bazy ( w każdej bazie jest taka sama) AB'=P-1ABP; EB'=P-1EBP=P-1P=EB.
Def: Operacji symetrycznej:
Operację A:Vn→Vn (n=2,3) nazywamy symetryczną⇔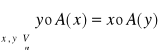
Def: Operacji antysymetrycznej:
Operację A:Vn→Vn (n=2,3) nazywamy antysymetryczną⇔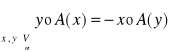
Def: Wartości własne i wektory własne:
Liczbę λ nazywamy wartością własną operacji liniowej A:V3→V3 (A: V2→V2) jeżeli istnieje niezerowy wektor
![]()
taki, że![]()
.Wektor![]()
nazywamy wektorem własnym odpowiadającym wart. własnej λ przy A.
Def. Tensor o walencji 1:
Dowolny obiekt nazywamy tensorem o welencji=1, nad przestrzenią Vn (n=2,3) jeżeli w każdej bazie B tej przestrzeni jest on określony jednoznacznie za pomocą n1 liczb xi zwanych współrzędnymi tensora w danej bazie, przy czym współrzędne te transformują się przy zmianie bazy według następującej zasady:
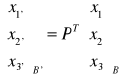
; (xi')=pii'xi
Def. Tensor o walencji 2:
Dowolny obiekt nazywamy tensorem o welencji=2, nad przestrzenią Vn (n=2,3) jeżeli w każdej bazie B tej przestrzeni jest on określony jednoznacznie za pomocą n2 liczb αij zwanych współrzędnymi tensora w danej bazie, przy czym współrzędne te transformują się przy zmianie bazy według następującej zasady: αi'j' =pii'pjj'αij
Tensor bezwładności: Jest on reprezentowany w bazie B przez macież
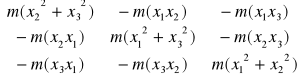
- Tensor bezwładnosci masy m Zaczepionej w punkcie M(x1,x2,x3)
Jest to tensor symetryczny na przekątnej są to momenty bezwładności m. względem osi wyznaczonej przez wektory bazowe: 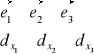
-moment względny x1,x2,x3
Pozostałe momenty to momenty dewiacyjne.
Def. Kwadryka:
Zbiór wszystkich punktów M(x1x2x3) o promieniach wodzących ![]()
i spełniających równanie ![]()
nazywamy kwadryką tensorową tensor TB. Kwadryka tensorowa jest to pewna powierzchnia .
Równanie kwadryki i w postaci macierzowej:![]()
Postać kanoniczna kwadryki tensorowej:
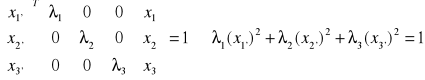
Rachunek operatorów:
Funkcja Heviside'a:
0 dla x<c
η(x-c)= 0,5 dla x=c
1 dla x>c
Def. Przekształcenie Laplace'a:
Przekształcenie Laplace'a funkcji f(x) zmiennej rzeczywistej x nazywamy funkcję F(s) zmiennej zespolonej s określoną wzorem:
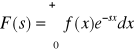
Jeżeli całka istnieje, to funkcję nazywamy transformatą Laplace'a funkcji f(x) i oznaczali będziemy symbolem:
F(s)=L[f(x)]
Def. Klasy oryginałów:
Mówimy, że funkcja f(x) przedziałami ciągła należy do klasy oryginałów gdy spełnia następujące warunki:
f(x)=0, dla x<0
f(x)=0,5(f(x+)+ f(x-))
Istnieją stałe M i α takie, że f(x)≤Meαx.
Twierdzenie o podobieństwie:
![]()
Twierdzenie o tłumieniu:
![]()
I. Twierdzenie o przesunięciu:
![]()
II. Twierdzenie o przesunięciu:
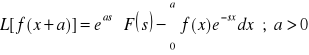
Tw. O Transformacji funkcji okresowej:
Jeżeli funkcja f(x) z klasy oryginałów jest funkcją okresową o okresie T dla wszystkich x∈R+ , to:
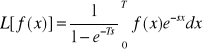
Najczęściej spotykane transformaty:
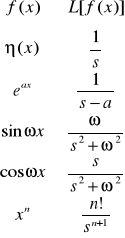
Liczby Zespolone:
Kryterium porównawcze:
Jeżeli ![]()
o wyrazach dodatnich jest zbieżny, to szereg Σzn jest bezwzględnie zbieżny.
Kryterium d'Alamberta:
Jeżeli 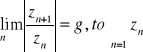
o wyrazach zespolonych jest bezwzględnie zbieżny gdy g<1, natomiast rozbieżny gdy g>1.
Kryterium Cauchy'ego:
Jeżeli ![]()
o wyrazach zespolonych jest bezwzględnie zbieżny gdy g<1, natomiast rozbieżny gdy g>1.
Tw. Warunek konieczny i dostateczny:
Warunkiem koniecznym i dostatecznym zbieżności Σzn o wyrazach zn=xn+yn do sumy S=S1+S2i jest jednoczesna zbieżność szeregów Σxn i Σyn odpowiedio do sum S1 i S2.
Def. Granicy według Heinego:
![]()
Def. Granicy według Cauchy`ego:
![]()
Def. Logarytm liczby zespolonej:
Liczbę zespoloną w=u+iv nazywamy logarytmem naturalnym z liczby zespolonej z=x+iy≠0 w =ln z, jeżeli ew=z, ln z=lnz+i(ϕ+2kπ).
Def. Pochodna funkcji zesoplonej:
Pochodną funkcji w=f(z) w punkcie z0 nazywamy granicę:
![]()
,jeżeli granica istnieje i jest skończona.
Def. Holomorficzność funkcji w punkcie:
Mówimy, że funkcja jest Holomorficzna, jeśli jest różniczkowalna w punkcie z0 i pewnym jego otoczeniu.
Def. Holomorficzność funkcji w obszarze D:
Mówimy, że funkcja jest holomorficzna w obszerze D, jeśli jest różniczkowalna w każdym punkcie tego obszaru.
Tw. Cauchy'ego-Riemana:
Jeżeli funkcja f(z)=u(x,y)+iv(x,y) ma pochodną w punkcie z0=x0+ iy0 ,to istnieją w tym punkcie pochodne cząstkowe części rzeczywistej u(x,y) i części urojonej v(x,y) oraz pochodne spełniają w tym punkcie równania:
![]()
Warunek konieczny, aby f(z) miała pochodną:
Jeżeli część rzeczywista u(x,y) i część urojona v(x,y) funkcji f(z)=u(x,y)+v(x,y) spełniają warunki Cauychego-Riemana w pewnym obszarze D i ponadto pochodne cząstkowe tych funkcji są ciągłe w tym obszarze, to funkcja f(z) w każdym punkcie a=x+iy tego obszaru pochodną f'(z) określoną wzorem:
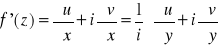
Rozwinięcia funkcji:
![]()
Wyszukiwarka
Podobne podstrony:
Algebra zbiorów, Ściągi dla studentów, Matematyka
zagadnienia matematyczne, Ściągi dla studentów, Matematyka
Matematyka - wzory, Ściągi dla studentów, Matematyka
Matematyka finansowa - wzory, Ściągi dla studentów, Matematyka
Postac iloczynowa trojmianu kwadratowego, Ściągi dla studentów, Matematyka
matematyka finansowa, Ściągi dla studentów, Matematyka
Matematyka - aproksymacja i interpolacja, Ściągi dla studentów, Matematyka
metody probablistyczne, Ściągi dla studentów, Matematyka
Ulamki egipskie, Ściągi dla studentów, Matematyka
analiza rentownosci, Ściągi dla studentów, Matematyka
Fraktale, Ściągi dla studentów, Matematyka
Algebra zbiorów, Ściągi dla studentów, Matematyka
pedagogika czasu wolnego - bielecka, Nauka, ściagi dla studentów turystyki i rekreacji ;)
więcej podobnych podstron