jądro: siły wiążące nukleony, stany energetyczne; wyprowadzić prawo absorpcji
rozpady jądrowe; wyprowadzić prawo rozpadu
Pomiary ilości promieniowania; promieniowanie naturalne
Magnetyczny rezonans jądrowy
Efekt Mossbauera
Analiza pierwiastkow metoda fluorescencji rentgenowskiej
Opis ruchu: def promienia wodzącego, prędkości i przyśpieszenia
Wektor wodzący, prędkość i przyśpieszenia w ruchu jednostajnym po okręgu
Podstawowe działania na wektorach: obliczyć sumę, różnicę iloczyn skalarny i wektorowy dwóch wektorów A=..., B=...
Zasady dynamiki
Napisać równanie ruchu masy na sprężynie i rozwiązać je
Różne obserwacje tego samego zjawiska: układy odniesienia; wyprowadzić transformację Galileusza
Układy inercjalne i nieinercjalne: wyprowadzić 2 zasadę dynamiki w układzie nieinercjalnym; siły bezwładności
Wyjaśnić stan nieważkości
Podać klasyczne prawa tarcia
Mechanizm tarcia na poziomie atomowym
Co to są zasady zachowania; wymienić i krótko opisać
Praca; wyprowadzić pracę potrzebną do rozciągnięcia sprężyny o L
Energia kinetyczna i twierdzenie o pracy i energii
Siły zachowawcze i energia potencjalna
Zachowanie energii mechanicznej
Zasada zachowania pędu; wyprowadzić zas. zach pędu dla dwóch zderzających się kulek
Zasada zachowania momentu pędu; wypowiedzieć i wyprowadzić 2 prawo Keplera
Wyjaśnić zjawisko precesji
zasada względności i jej konsekwencje
zegar świetlny: udowodnić, że stałość prędkości światła wymaga, by czas płynął inaczej w różnych układach odniesienia
Stałość przedziału czasoprzestrzennego i analogia z odległością
W rakiecie poruszającej się z prędkością V, wzdłuż osi x' leży pręt o długości L'. Jaką długość tego pręta zaobserwuje obserwator w układzie nieruchomym?
Sformułować i wyjaśnić paradoks bliźniąt
Napisać i omówić transformację Lorentza. Dowieść, że dla małych prędkości przechodzi ona w transformację Galileusza.
Energia i pęd relatywistyczny. Co to jest masa relatywistyczna i masa spoczynkowa. Dla jakiej prędkości masa relatywistyczna ma wartość 2 razy większą, niż masa spoczynkowa
Zasady powstawania i kontroli obrazu w monitorze klasycznym
Co to jest polaryzacja światła; w jaki sposób światło można spolaryzować
Ciekłe kryształy i ich wykorzystanie w konstrukcji wyświetlaczy
Masa atomowa pierwiastka; od czego zależy masa atomowa
Co to jest funkcja falowa; jaka jest jej interpretacja i jak się ją oblicza? Jakie liczby kwantowe określają funkcję falową dla atomu wodoru
Model Bohra atomu wodoru
Stany energetyczne atomu wodoru wg. Bohra i wg. modelu kwantowo mechanicznego
Stany energetyczne atomów o wyższych liczbach Z
Dlaczego układ Mendelejewa nazywa się układem okresowym; z czym wiążą się rzędy i kolumny
Wyprowadzić równanie stanu gazu doskonałego; co to jest temperatura bezwzględna?
Zasada ekwipartycji energii. Wykorzystać tą zasadę do obliczenia ciepła właściwego gazu o różnej liczbie stopni swobody
Sposoby wymiany energii między układami; I zasada termodynamiki
W jakich warunkach energia wewnętrzna układu może być przekształcona na pracę użyteczną; entropia i II zasada termodynamiki.
45.Wyprowadzić wzór na sprawność idealnego silnika cieplnego
Jądro: siły wiążące nukleony, stany energetyczne; wyprowadzić prawo absorpcji
Każde jądro atomowe składa się z protonów i neutronów wiązanych siłami jądrowymi, niezależnymi od ładunku.
Ponieważ neutron i proton mają prawie taką samą masę i bardzo zbliżone inne własności, więc obydwa określa się wspólną nazwą nukleon. Łączną liczbę protonów i neutronów w jądrze nazywamy liczbą masową jądra i oznaczamy literą A. Liczba neutronów jest dana równaniem A - Z, gdzie Z jest liczbą protonów zwaną liczbą atomową.
Wartość liczby A dla jądra atomowego jest bardzo bliska masie odpowiadającego mu atomu.
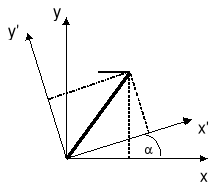
Aby wyjaśnić co tak silnie wiąże nukleony w jądrach atomowych trzeba wprowadzić nowe oddziaływanie. Ta siła wiążąca musi być większa niż siła odpychania elektrostatycznego występująca pomiędzy protonami. Określamy ją mianem siły jądrowej lub oddziaływania silnego. Potencjał opisujący to oddziaływanie jest o rząd wielkości większy niż energia potencjalna elektrostatycznego odpychania proton - proton. Sytuacja ta jest pokazana na rysunku poniżej
.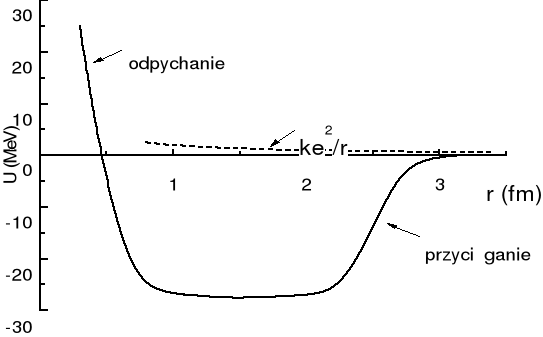
Oddziaływanie proton - proton, proton - neutron i neutron - neutron jest identyczne (jeżeli zaniedbamy relatywnie małe efekty odpychania elektrostatycznego) i nazywamy go oddziaływaniem nukleon - nukleon.
Prawo absorpcji
Dotyczy każdego rodzaju promieniowania
N N-dN
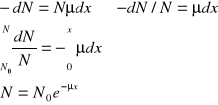
2. Rozpady jądrowe; wyprowadzić prawo rozpadu
Rozpady jądrowe zachodzą zawsze (prędzej czy później) jeśli jądro o pewnej liczbie nukleonów znajdzie się w stanie energetycznym, nie będącym najniższym możliwym dla układu o tej liczbie nukleonów.
Takie nietrwałe (w stanach niestabilnych) jądra powstają w wyniku reakcji jądrowych. Niektóre reakcje są wynikiem działań laboratoryjnych, inne dokonały się za sprawą przyrody podczas powstawania naszej części Wszechświata. Jądra nietrwałe pochodzenia naturalnego są nazywane promieniotwórczymi, a ich rozpady noszą nazwę rozpadów promieniotwórczych (promieniotwórczości).
rozpad alfa
Występujący zazwyczaj w jądrach o Z ≥ 82. Rozpad α polega na przemianie niestabilnego jądra w nowe jądro przy emisji jądra 4He tzn. cząstki α.
Proces zachodzi samorzutnie bo jest korzystny energetycznie. Energia wyzwolona w czasie rozpadu (energetyczny równoważnik niedoboru masy) jest unoszona przez cząstkę α w postaci energii kinetycznej.
Przykładowa reakcja dla jądra uranu wygląda następująco
238U 234Th + 4He + 4.2 MeV
Rozpatrzmy teraz układ zawierający w chwili początkowej wiele jąder tego samego rodzaju. Jądra te podlegają rozpadowi α (równie dobrze rozpadowi β) z częstością rozpadów . Chcemy znaleźć liczbę jąder, która nie uległa rozpadowi po czasie t od chwili początkowej.
Oznaczamy przez N liczbę jąder. Wtedy dN (<0) oznacza liczbę jąder, które rozpadają się w czasie dt.
Spodziewana liczba rozpadów (liczba jąder, które się rozpadną) w czasie dt tzn. (t, t + dt) jest dana wyrażeniem
dN = - Ndt
gdzie znak minus wskazuje, że dN jest liczbą ujemną czyli, że N maleje z czasem.
Możemy rozdzielić zmienne i scałkować równanie obustronnie
![]()
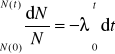
![]()
czyli
![]()
skąd
![]()
N(0) jest liczbą jąder w chwili t = 0, a N(t) liczbą jąder po czasie t.
Powyższy wzór nazywamy wykładniczym prawem rozpadu.
Często wyraża się N(t) poprzez średni czas życia jąder, który z definicji jest równy odwrotności częstości rozpadów; τ = 1/λ.
Prawo rozpadu przyjmuje wtedy postać
N = N0e-t/τ (38.2)
Do scharakteryzowania szybkości rozpadu używa się czasu połowicznego rozpadu (zaniku) T1/2. Jest to taki czas, po którym liczba jąder danego rodzaju maleje do polowy tzn. N = (1/2) N0. Wstawiając to do równania (38.2), otrzymujemy
![]()
czyli
![]()
skąd
T1/2 = 0.693 τ (38.3)
Przykładowo dla 238U czas połowicznego zaniku wynosi 4.5·109 lat, a dla 212Po jest rzędu 10-6 promieniowanie γ
Jeśli jądro jest wzbudzone do wyższego stanu energetycznego, to może nastąpić samoczynna emisja fotonu i przejście do niższego stanu energetycznego. Ponieważ odległości między poziomami energetycznymi w jądrach są rzędu MeV więc fotony emitowane przez jądra mają energię tysiące razy większą od energii fotonów wysyłanych przez atomy. Takie wysokoenergetyczne fotony emitowane przez jądra nazywamy promieniowaniem γ.
Jądra w stanie wzbudzonym można łatwo otrzymać używając neutronów o małej energii. Jeżeli taki powolny neutron przechodzi np. przez bryłkę uranu 238U to zawsze gdy znajdzie się blisko jądra działa na niego siła przyciągająca wywołana przez oddziaływanie jądrowe. Dlatego jest bardzo prawdopodobne, że taki neutron zostanie wychwycony i powstanie jądro 239U* w stanie wzbudzonym (oznaczone *). Takie jądro przechodzi do stanu podstawowego emitując jeden lub kilka kwantów γ. Proces ten opisują następujące reakcje jądrowe:
n + 238U 239U*
c. rozpad β
Badając własności promieniotwórczości stwierdzono, że istnieją trzy rodzaje promieniowania α, β, γ. Po dalszych badaniach stwierdzono, że α to jądra helu, promienie γ to fotony, a promienie β to elektrony lub pozytony (cząstka elementarna dodatnia o masie równej masie elektronu).
Jądra, których ilość protonów Z różni się od wartości odpowiadającej stabilnym jądrom o tej samej liczbie masowej A, mogą zmieniać Z w kierunku jąder stabilnych poprzez rozpad β. Współczesna teoria rozpadów β została rozwinięta przez Fermiego w 1931 r.
Najprostszym przykładem rozpadu β jest rozpad swobodnego neutronu zachodzący z czasem połowicznego zaniku 12 minut
![]()
Neutron rozpada się na proton, elektron i antyneutrino (cząstka elementarna o zerowym ładunku i zerowej masie spoczynkowej).
Inny przykład to omawiany już uran 239U; rozpad zachodzi z czasem połowicznego zaniku 24 minuty
![]()
Powstały izotop też nie jest trwały i podlega rozpadowi β
![]()
z czasem połowicznego zaniku 2.35 dnia.
W takim procesie liczba Z wzrasta o jeden a liczba A pozostaje bez zmiany.
Innym rozpadem β, jest proces, w którym jądra emitują pozytony, a towarzyszy temu zawsze emisja neutrina. W tym procesie liczba Z maleje o jeden, a liczba A pozostaje bez zmiany.
239U* 239U + γ
3. Pomiary ilości promieniowania; promieniowanie naturalne
Naturalna promieniotwórczość polega na samorzutnej przemianie jądra z emisją jądra helu ![]()
(cząstki ![]()
) albo elektronu (cząstki![]()
). W wyniku przemiany-rozpadu promieniotwórczego-powstaje powstaje jądro w stanie wzbudzonym. Jądro to, przechodząc do niższego stanu energetycznego, emituje krótkofalowe promieniowanie elektromagnetyczne(kwanty![]()
)Jedynie 30% ogółu promieniowania na Ziemi pochodzi ze źródeł sztucznych (wytworzonych przez człowieka). Większość stanowią źródła naturalne takie jak promieniowanie kosmiczne czy pierwiastki występujące w glebie. Napromieniowanie ze źródeł naturalnych - 2,4 mSv
z gleby - 0,4 mSv 1. Promieniowanie kosmiczne -0,4mSv
2. Promieniowanie
3. Pierwiastki radioaktywne wchłaniane lub wdychane - 1,6mSv
Napromieniowanie ze źródeł sztucznych - 1,1mSv 4. Napromieniowanie pochodzenia medycznego -1mSv 5. Działalność przemysłowa - 0,1mSv |
|
Napromieniowanie pochodzenia medycznego stanowi przeciętną dawkę około 1 mSv bardzo nierównomiernie rozłożoną w populacji. Promieniowanie to pochodzi przede wszystkim z prześwietleń rentgenowskich, czy radioterapii. Działalność przemysłowa odpowiada przeciętnej dawce około 0,1 mSv, w tym jedynie 0,02 mSv przypada na energię jądrową. Promieniowanie kosmiczne, jak sama nazwa wskazuje, dochodzi do Ziemi z przestrzeni kosmicznej. Większą jego część stanowi promieniowanie emitowane na Słońcu w drodze przemian jądrowych. Dawka tego promieniowania zmienia się wraz z wysokością, na której się znajdujemy. Pierwiastki radioaktywne zawarte w glebie, głównie uran, tor i potas dają przeciętnie napromienienie dawką 0,4 mSv rocznie, i jest ona bardzo zróżnicowana w zależności od rodzaju gleby. Pierwiastki radioaktywne wchłaniane podczas oddychania lub z pokarmem, takie jak radon-222, który jest naturalnym gazem pochodzącym z rozpadu uranu zawartego w glebie i głównym źródłem naturalnego napromieniania, czy potas w żywności, który częściowo zatrzymywany jest w naszym organizmie, powodują napromienienie dawką około 1,6 mSv rocznie. : |
|
Pomiary ilości promieniowania
Różnego rodzaju promieniowanie różnie wpływa na żywe organizmy
Aktywność izotopu:liczba rozpadów w jednostce czasu[Bq]-(bekerel)
Dawka pochłonięta D0: energia zaabsorbowana przez 1 kg substancji[Gy]-(grej)
Równoważnik dawki H=D0 *Q (gdzie:Q-współ. jakości)
dawka absorbowana dowolnego promieniowania wywołująca ten sam skutek co pochłonięta dawka promieni X
jednostka : 1Sv (siwert) =100 rem (remów)
4. Magnetyczny rezonans jądrowy
Zjawisko absorpcji fal elektromagnetycznych o częstotliwości radiowej przez jądra atomowe substancji stałych, ciekłych lub gazowych(o momencie magnetycznym różnym od zera), pod wpływem stałego pola magnetycznego
Jądro posiada moment magnetyczny
![]()
= ![]()
Ih, ![]()
- współczynnik giromagnetyczny
![]()
= gNµNI, gN - czynnik jądrowy
W stałym zewnętrznym polu magnetycznym B0 na moment magnetyczny wywierana jest para sił powodując jego precesje o częstości
Wprowadza się dodatkowe zewnętrzne, przemienne pole magnetyczne B
Jeżeli
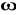
= częstość pola B -> rezonans magnetyczny ->przekaz energii do układu pole magnetyczne stałe-moment magnetyczny.
określa się wzorem
=
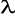
B0 -> zmieniając B0 możemy uzyskać częstość precesji zgodną z częstością pola magnetycznego B (można także zmieniać częstość pola przy stałym B0)
W wyniku rezonansu następuje zmiana rzutu momentu µ na kierunek B0 przy czym rzut wektora µ musi być równy liczbie kwantowej M.I = I,.....,+I. (przeskok momentu µ z pozycji A do pozycji C)
Następuje zmiana energii E momentu µ w polu zewnętrznym B0
E=-µ•B0=-gNµNMIB0 -> ![]()
E=gNµNB0 , ponieważ ![]()
M=+/-1
Zmiana energii momentu magnetycznego w polu B0 może nastąpić na skutek przekazu kwantu promieniowania elektromagnetycznego h![]()
Warunek rezonansu:
h![]()
= gNµNB0, gN- czynnik jądrowy
W praktyce wyznacza się gN zmieniając B0 i utrzymując stałą częstotliwość.
5. Mössbauera zjawisko, zjawisko bezodrzutowej emisji kwantów gamma przez jądro atomu znajdującego się w sieci krystalicznej, jest to możliwe, gdy energia odrzutu jądra po wysłaniu kwantu gamma przekazana zostaje całej sieci krystalicznej. Zjawisko zachodzi również dla pochłaniania promieniowania gamma.Bezodrzutowa emisja prowadzi do małych szerokości naturalnych linii widmowych (szerokość względna aż do rzędu 10-15). W tych warunkach absorpcja promieniowania ma charakter rezonansowy, małe zmiany energii fotonu (rzędu szerokości linii) wpływają drastycznie na prawdopodobieństwo absorpcji, np. nawet powolny ruch źródła względem próbki zaburza proces (Dopplera zjawisko).
Zaburzenie takie może być skompensowane przez inne zaburzenie wywołane jakimś badanym procesem, umożliwia to prowadzenie analiz takich zjawisk, jak wpływ lokalnego pola wewnątrzkrystalicznego na poziomy energetyczne w jądrze (Zeemana zjawisko), rodzaje i energia drgań sieci krystalicznej, wpływ pola grawitacyjnego Ziemi na energię fotonu, zmiana rozmiarów atomu w stanie wzbudzonym itp.
Poziomy energetyczne jądra mogą zależeć od jego otoczenia w sieci krystalicznej
Nie symetryczne pole E
Spin jądra=3/2
Spin jądra=1/2
Poziomy energii
Informacja o polu elektrycznym w miejscu jądra
Nie symetryczne pole B
Spin jądra=3/2
Spin jądra=1/2
Poziomy energii
informacja o polu magnetycznym w miejscu jądra
6. Fluorescencja, zjawisko przejścia cząsteczki z poziomu zerowego wzbudzonego stanu singletowego S1 na dowolny poziom oscylacyjno-rotacyjny stanu podstawowego S0. Widmo fluorescencji jest przesunięte w kierunku fal dłuższych w stosunku do widma absorpcji. Czas życia fluorescencji wynosi ok. 10-8 s.
Fluorescencja rentgenowska, metoda analiz chemicznych, polega na pobudzaniu rentgenowskiego promieniowania charakterystycznego danego materiału poprzez umieszczenie go w strumieniu wysokoenergetycznych fotonów (kwantów gamma lub promieni rentgenowskich z lampy rentgenowskiej). Energia padających fotonów musi być wyższa od energii analizowanego promieniowania charakterystycznego. Do rejestracji promieniowania fluorescencji rentgenowskiej stosuje się obecnie spektrometry rentgenowskie z detektorami półprzewodnikowymi. Odpowiednia kalibracja spektrometru pozwala przejść od obserwowanych natężeń linii widmowych promieniowania charakterystycznego do koncentracji pierwiastków w badanym materiale. Promieniowanie Rentgena jest wynikiem przejść elektronów do niższych stanów energetycznych w atomie. Aby emitować promienie X atom może być wzbudzony przez promieniowanie o wyższej energii.
Ponieważ w metodzie fluorescencji rentgenowskiej źródłem „światła” jest powłoka K (najniższa), dlatego widmo promieniowania jest charakterystyczne dla atomu, bez względu na jego otoczenie
Rentgenowska analiza spektralna, metoda analizy ilościowej i jakościowej zawartości pierwiastków chemicznych w próbce, w której to analizie wykorzystuje się promieniowanie charakterystyczne, emitowane przez pobudzane atomy próbki.
Rozróżnia się różne metody rentgenowskiej analizy spektralnej w zależności od rodzaju pobudzenia (np. PIXE, rentgenowska fluorescencja).
Źródło próbka
Licznik proporcjonalny
7. Opis ruchu:
Ruchu jest to zmiana położenia jednego ciał względem innych ciał, które nazywamy układem odniesienia. To samo ciało może poruszać się względem jednego układu odniesienia a spoczywać względem innego. Oznacza to, że ruch jest pojęciem względnym. W przypadku ogólnym ruch będzie wyznaczony przez podanie trzech równań ruchu:x=f1(t), y=f2(t), z=f3(t). Zamiast tych trzech równań dla współrzędnych ruchomego punktu materialnego można określić jego ruch jednym tylko równaniem wektorowym r=r(t)=r(x(t),y(t),z(t)) gdzie r-promień wodzący poprowadzony z początku układu współrzędnych
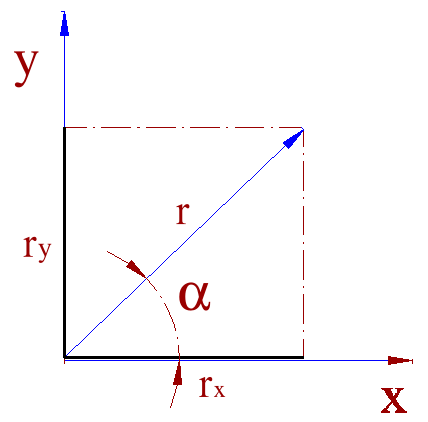
![]()
;
![]()
;
![]()
Prędkość
Prędkość jest zmianą odległości w jednostce czasu.
Prędkość stała
Jeżeli ciało, które w pewnej chwili t0 znajdowało się w położeniu r0, porusza się ze stałą prędkością v to po czasie t znajdzie się w położeniu r danym związkiem r-r0 = v(t-t0) czyli ![]()
Prędkość chwilowa
Jeżeli obiekt przyspiesza lub zwalnia to wskazania szybkościomierza nie zgadzają się ze wyrażeniem chyba, że weźmiemy bardzo małe wartości r - r0 (Δr) czyli również bardzo małe t-t0 (Δt). Stąd prędkość chwilowa: ![]()
. Takdefiniuje się pierwszą pochodną, więc
![]()
Prędkość średnia
Wektorem średniej prędkości vśr ruchu punktu w przedziale czasu od t do t+t nazywamy stosunek przyrostu r promienia wodzącego punktu w ciągu tego przedziału czasu do przyrostu czasu t .
![]()
Przyspieszenie
Przyspieszenie to tempo zmian prędkości.Prędkość zmienia się jednostajnie z czasem czyli przyspieszenie jest stałe.Analogicznie jak wektor prędkości, definiujemy wektor przyśpieszenia:
![]()
Gdy przyspieszenie zmienia się z czasem musimy wtedy ograniczyć się do pomiaru zmian prędkości Δv w bardzo krótkim czasie Δt (analogicznie do prędkości chwilowej). Odpowiada to pierwszej pochodnej v względem t.
![]()
Przyśpieszenie jest więc druga pochodną wektora wodzącego.
8.Ruch jednostajny po okręgu
Szczególnym przypadkiem ruchu po torze krzywoliniowym jest ruch po okręgu. Jeżeli długość wektora jest stała v=const, toruch taki nazywamy ruchem jed. po okręgu. Wektor v w ruchu tym nie jest stały, gdyż zmienia się jego kierunek, przy czym jest on zawsze styczny do okręgu
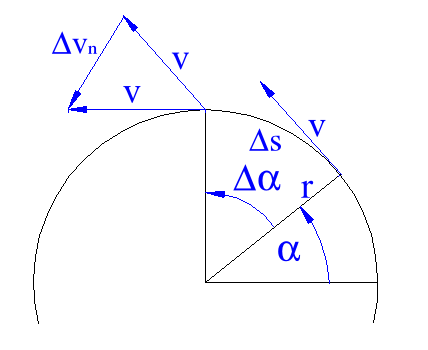
Gdy oznaczymy przez s element łuku odpowiadający kątowi zakreślonemu przez promień okręgu r w czasie t otrzymamy s=r Wiemy, że prędkość ![]()
, gdzie s jest współrzędną łukową. Podstawiając za s wyrażenie r otrzymamy![]()
![]()
![]()
. Pochodną kąta względem czasu nazywamy prędkością kątową i oznaczamy przez a więc ![]()
. Ze wzorów wynika , że ![]()
czyli prędkość liniowa v w ruchu jednostajnym po okręgu jest równa iloczynowi prędkości kątowej przez promień.
W ruchu jed. po okręgu występuje geometryczny przyrost prędkości vn powodujący wyłącznie zmianę kierunku prędkości a nie jej wartości liczbowej. Stosunek vn do czasu t, w którym ten przyrost nastąpił nazywamy przyśpieszeniem dośrodkowym lub normalnym przy czym ![]()
. Iloraz ![]()
. Gdy t—0 otrzymamy ![]()
.Wektor wodzący r(t)=Rcos(ωt) x+Rsin(ωt) y
9.Podstawowe działania na wektorach: obliczyć sumę, różnicę iloczyn skalarny i wektorowy dwóch wektorów A=..., B=..
Uwaga Wszystkie wektory to np. a = ![]()
; b = ![]()
; c = ![]()
Wektorem nazywamy uporządkowaną parę punktów. Graficznie przedstawia się go w postaci odcinka zakończonego strzałką.
Każdy wektor posiada :
Kierunek - prosta na której wektor leży
Zwrot - określony przez grot strzałki wektora
Wartość - długość wektora w określonej skali
Dodawanie wektorów
a+b=c
metoda trójkąta
Metoda równoległoboku
a=(x1 y1 z1)
b=( x2 y2 z2)
a+b=( x1 +x2 ;y1 +y2 ;z1 +z2)=c
Odejmowanie wektorów
c=a-b=a+(-b) c=a-b
Równoległość
B=(Bx x +By y)=cA=c(Ax x+ AY y) y
A
B=cA
x
Długość wektora
Iloczyn wektorowy
A × B = z |A| |B| sin =
10. Zasady dynamiki
I ZASADA DYNAMIKI (zasada bezwładności)
Jeśli na ciało nie działa żadna siła, lub działające siły się równoważą, to ciało porusza się ruchem jednostajnym (a więc i prędkość jest stała co do wartości i co do kierunku).
V=const jeśli ΣFi=0
F1+F2+F3=0 - Ruch po prostej ze stałą prędkością: wypadkowa siła=0
V = constans - Ruch „jednostajny” po okręgu : wypadkowa siła różna od zera
Jeśli V ciała jest const, to przedmioty względem których ruch tego ciała jest opisany (czyli układ współrzędnych ) jest układem inercjalnym
II ZASADA DYNAMIKI
Pęd to iloczyn masy i prędkości. Pęd jest wektorem!
p=mV, p= Σmi Vi
Jeśli na ciało działają siły, to ciało zmienia swój pęd z szybkością proporcjonalną do siły wypadkowej (wektorowej sumy sił).
Jeśli masa nie zależy od czasu, to ΣFi=ma
Ruch po okręgu |V| = constans F = ma, |F| =(m V2)/R
Nie wiemy nic o sile, oprócz tego, że jeśli działa, to zmienia pęd ciała
III ZASADA DYNAMIKI III zasada inaczej: akcja = reakcji
Częściowo wskazuje na własności siły
Jeżeli jedno ciało (ciało 1) działa na drugie (ciało 2) siłą F12 , to drugie ciało działa na pierwsze siłą F21 przeciwnie skierowaną do F12 gdzie indziej przyłożoną (do ciała 1), lecz o tej samej długości.
11. Napisać równanie ruchu masy na sprężynie i rozwiązać je
Jeśli sprężyna (lub dowolne ciało sprężyste) zostanie odkształcone , o wektor r od położenia równowagi to pojawia się siła tym większa , im większe to odkształcenie i zmierzająca do zniwelowania tego ` odkształcenia F2= -kr (k-stała sprężystości)
F2= -kx
r Σ Fi=ma II zasada dynamiki
F1= mg mg+(-kr)=ma równanie ruchu w postaci wektorowej
Równanie ruchu zrzutowane na oś x
x=x0+A sin (ωt) propozycja rozwiązania
k(x0+A sin (ωt))-mg=-mω 2Asin (t) Sprawdzenie
-kx0-mg=-0
A sin (ωt)(-k+mω2 )=0
x0 =-mg/k
ω2= k/m ; T=2π![]()
12. Transformacja Galileusza
Układem inercjalnym nazywamy taki układ, w którym stosują się zasady dynamiki Newtona
Za taki układ możemy uważać ziemię i wszelkie układy nieruchomo z nią związane. Układem inercjalnym jest również układ poruszający się ruchem jednostajnym prostoliniowym względem układu inercjalnego, natomiast układ poruszający się ruchem zmiennym względem układu inercjalnego nie jest układem inercjalnym.
y y' v
xo =vt
O O'
x x'
z z'
Przy zmianie współrzędnych x, y , z i czasu t na współrzędne x', y', z' i ,t' obowiązuje transformacja Galileusza. Jeżeli układ x', y', z' porusza się w kierunku osi x ruchem jednostajnym postępowym z prędkością stałą v przy czym osie x', y', z' pozostawały równoległe do x, y, z a w chwili t=0 układy pokrywały się i czas w obu układach płynie tak samo czyli t = t' . W tych warunkach (ujęciu Newtonowskim) pewne zdarzenie które w układzie X,Y,Z miało współrzędne czasowo-przestrzenne ( x, y , z ,t) będzie miało w układzie przestrzennym współrzędne (x', y', z', t')
x' = x - vt y' = y z' = z t' = t ---równania te noszą nazwę Transformacji Galileusza
13. Układy inercjalne i nieinercjalne: wyprowadzić II zasadę dynamiki w układzie nieinercjalnym; siły bezwładności
Inercjalny układ odniesienia, układ odniesienia należący do wyróżnionej klasy układów, w których spełniona jest pierwsza zasada dynamiki Newtona. Istnienie inercjalnego układu odniesienia jest postulatem mechaniki klasycznej. Wszystkie prawa fizyki mają taką samą postać w każdym inercyjnym układzie odniesienia. Każdy układ poruszający się względem inercjalnego układu odniesienia też jest ukł. inercjalnym.
Jest to układ w którym ciało na którego nie działają żadne siły porusza się w tym układzie ruchem jedn. i prostoliniowym lub też znajduje się w spoczynku.
Nieinercjalny układ odniesienia, fizyczny układ odniesienia, w którym nie jest spełniona I zasada Newtona np. układ związany z obracającym się ciałem (w szczególności układ związany z Ziemią) lub ciałem poddanym przyspieszeniom liniowym. Przeciwieństwo układu odniesienia inercjalnego. W nieinercjalnym układzie odniesienia obserwuje się np. siłę Coriolisa, siłę odśrodkową, inne siły bezwładności.
W układzie tym ciało porusza się z przyspieszeniem także w takim przypadku gdy nie oddziałuje ono z innymi ciałami.
(RYS)
Załóżmy, że układ x, y, z jest układem inercyjnym a układ x', y', z' porusza się względem niego ruchem postępowym z przyspieszeniem a0 czyli v0 ≠constans. Układ x', y', z' jest więc układem nie inercjalnym . Punkt materialny P, którego przyspieszenie w układzie x, y, z, wynosi a w układzie x', y', z' poruszającym się ruchem postępowym przyspieszonym ma przyspieszenie :
a1=a-a0
mnożąc obie strony równania przez masę m punktu materialnego otrzymujemy
ma1=ma-ma0
gdzie ma = F -siła działająca na punkt materialny w układem nie inercjalnym
a więc F1=F-ma lub F1=F+Fb
W układzie przysp. Występuje zatem dodatkowa siła Fb=-ma0 gdzie a0-jest przyspieszeniem układu nie inercjalnego w ruchu postępowym względem ukł. inercjalnego (przysp.unoszenia). Siłę Fb nazywamy siłą bezwładności lub siłą oporu bezwładnego. Mierząc ją możemy wyznaczyć przyspieszenie układu nie inercjalnego.
W codziennym życiu spotykamy się często z siłami bezwładności np. jazda tramwajem lub autobusem. Gdy pojazd rusza działa na nas siła przeciwnie skierowana do zwrotu przyspieszenia(kier. jazdy).O realności sił bezwładności mówi nam dośw. z windą. Na podłodze stawiamy wagę sprężynową która podczas postoju pokazuje ten sam ciężar odważnika. Natomiast jeżeli winda jedzie w górę lub hamuje jadąc w dół to ciężar odważnika jest jakby większy, a gdy winda jedzie w dół lub hamuje jadąc w górę ciężar odważnika jakby się zmniejszał.
Z siłami bezwładności spotykamy się przy obserwowaniu zjawisk związanych z ruchem przyspieszonym. Siła bezwładności różni się zasadniczo od zwykłych sił . Zwykłe siły wiążą się zawsze z działaniem na poruszające się ciało innych ciał materialnych. Siła bezwładności natomiast nie pochodzi od żadnych ciał materialnych a jej istnienie jest spowodowane tylko faktem wyboru nieinercjalnego układu odniesienia. Dlatego siłę tą nazywamy często siłą pozorną.
14.Wyjaśnić stan nieważkości
Ciało jest w stanie nieważkości, jeżeli w żaden sposób nie przeciwdziałamy sile grawitacji.
Sytuacja taka ma miejsce w spadku swobodnym, o ile można zaniedbać inne
siły, jak np. opór powietrza, lub zrównoważyć ich działanie.
Na co dzień siła grawitacji jest równoważona reakcją podłoża. Wystarczy jednak podskoczyć, żeby na moment znaleźć się w stanie nieważkości (przy prędkościach uzyskiwanych przy podskakiwaniu opór powietrza jest zaniedbywalny).
Najbardziej znanym przykładem spadku swobodnego jest ruch po orbicie, np. okołoziemskiej.
W zasadzie niczym nie różni się od rzutu kamieniem. Jedyne różnice to brak oporu powietrza (jeżeli orbita jest powyżej atmosfery) i to że ,,orbita'' kamienia przecina powierzchnię Ziemi (gdzie ruch się kończy), a orbita satelity tej powierzchni nie przecina (bo prędkość satelity jest wystarczająco duża).
Inny przykład uzyskania stanu nieważkości na dłuższy czas (kilka minut) to tzw. loty balistyczne samolotem. Samolot najpierw rozpędza się, a następnie pozwala się mu ,,swobodnie spadać'', używając silników do jak najdokładniejszego równoważenia oporu powietrza (używa się do tego odpowiednio zaprogramowanego autopilota). Dzięki temu samolot spada, jakby powietrza nie było. Oczywiście należy tę zabawę przerwać zanim tor lotu przetnie powierzchnię Ziemi. :-) I to na tyle wcześnie, żeby wyprowadzenie z lotu nurkowego nie wymagało użycia przyspieszeń zagrażających życiu załogi.
Nieważkość, stan, w którym działające na ciało siły zewnętrzne nie wywołują wzajemnych ciśnień jego cząstek na siebie, a ciśnienia wywołane własnymi siłami grawitacji są właściwie równe zeru ze względu na małą masę. Nieważkość występuje np. przy swobodnym spadaniu ciał, gdy nie działają inne siły zewnętrzne poza grawitacyjnymi (np. opór powietrza), a więc na orbitach sztucznych satelitów i planetoid. Na Ziemi nieważkość można uzyskać na okres ok. 1 min. w samolocie poruszającym się po torze keplerowskim. Można też symulować ją w naśladownikach. Wpływ nieważkości na żywe organizmy przejawia się wrażeniem spadania, zawrotami głowy, nudnościami, zakłóceniami w działaniu układu krążenia, trudnościami w wykonywaniu ruchów (hipodynamia, hipokinezja) i ich koordynacji, odwapnieniem kości
15.Podać klasyczne prawa tarcia
I prawo tarcia:
Siła tarcia , która przeciwdziała przesuwaniu stykających się ze sobą powierzchni jest proporcjonalna do siły dociskającej powierzchnie
1.Klocek nieruchomy-tarcie jest równe max. sile przeciwdziałającej się ruchowi.
2.Klocek ruchomy-tarcie jest równe sile podtrzymującej ruch jednostajny
(RYS)
Równia pochyła(RYS)
1.przypadek gdy klocek jest nieruchomy
W miarę wzrostu kąta C rośnie siła Gx powodująca ruch w dół, czyli rośnie też siła tarcia
2.przypadek gdy klocek jest ruchomy
W miarę wzrostu kąta α maleje siła sprężystości podłoża N czyli tarcie również maleje.
N=Gy Gy=G*cosα
T=fk*N=fk*G*cosα
II prawo tarcia: nieruchomy
Siła tarcia nie zależy od powierzchni styku
(RYS)
III prawo tarcia:
Z chwilą wprowadzenia ciała w ruch siła tarcia nie zależy od prędkości.
(RYS)
16.Mechanizm tarcia na poziomie atomowym
Tarcie w skali atomowej ma niewiele wspólnego z makroskopową chropowatością powierzchni np. w niektórych przypadkach suche powierzchnie są bardziej śliskie niż mokre.
Również makroskopowych praw tarcia nie da się zastosować w skali atomowej...
Mikroskopowe prawa tarcia:
I prawo:
Siła tarcia jest proporcjonalna do rzeczywistej, a nie obserwowanej powierzchni styku. Jeśli rośnie nacisk to rośnie też powierzchnia styku i dlatego tarcie jest proporcjonalne do nacisku.
(RYS)
II prawo:
Siła tarcia zależy od tego jak łatwo dwie powierzchnie sklejają się w porównaniu z procesem rozdzielenia ich.
III prawo:
Siła tarcia jest wprost proporcjonalna do prędkości przesuwania się rzeczywistych punktów styku.
Makroskopowych praw tarcia nie da się zastosować w skali atomowej. ale dzięki zrozumieniu sił tarcia w skali atomowej możliwe jest zmniejszenie tarcia w skali makroskopowej czego przykładem są na przykład nanołożyska.
Możliwe jest tarcie bez zużycia materiału.
17. Co to są zasady zachowania; wymienić i krótko opisać
Zasady zachowania są to prawa dotyczące stałości pewnych parametrów charakteryzujących układ fizyczny. Do najważniejszych należą zasady zachowania:
Energii = w każdym izolowanym układzie fizycznym całkowita suma energii jest stała(nie zmienia się w czasie)
Pędu = całkowity wektorowy pęd układu izolowanego jest zachowany przez każdy rodzaj oddziaływań fizycznych
Moment pędu = jeśli wypadkowy moment sił zewnętrznych działających na ciało jest równy zeru, wówczas jego moment pędu ma wartość stałą
Ładunku = różnica liczby ładunków elektrycznych dodatnich i ujemnych danego układu jest stała bez względu na rodzaj oddziaływań zachodzących w układzie.
Pewne wielkości we Wszechświecie (lub jego wyodrębnionej części) nie zmieniają się w czasie - są zachowane. Prawa, które mówią w jakich okolicznościach te wielkości są zachowane (czyli zasady zachowania) stanowią ograniczenie na jakiekolwiek zjawisko w przyrodzie : nic co nie jest z nim zgodnie nie może się zdarzyć.
Zasady zachowania są konsekwencją symetrii we wszechświecie
Zasada zachowania pędu symetria względem przesunięć
Zasada zachowania momentu pędu symetria względem obrotów
Zasada zachowania energii symetria względem czasu
18. Praca; wyprowadzić pracę potrzebną do rozciągnięcia sprężyny o L
Praca stałej siły F przesuwającej ciało o wektor x wynosi:
L = F*x
Jeśli siła F jest stała tylko na małych drogach x to całkowita praca na skończonym odcinku wynosi: L=ΣF· x
czyli jest to pole pod krzywą F(x)
Jednostka pracy w SI to [dżul]
Praca jest wielkością fizyczną skalarną L zdefiniowaną wzorem
Siła wywierana przez sprężynę jest siłą przywracającą równowagę i wynosi F = -k x.
Aby rozciągnąć sprężynę musimy przyłożyć siłę równą co do wartości lecz przeciwnie skierowaną. Tak więc F = k x. Jaką pracę wykonujemy?
siła sprężysta: F = -k x
Praca siły sprężystej to
19. Energia kinetyczna i twierdzenie o pracy i energii
Skoro energię ciała można zwiększyć wykonując nad nim pracę, to wykonajmy pracę nad początkowo nieruchomym ciałem
Indeksy całek ra rb
ponieważ d(V·V)=
V ·dV+dV ·V=2V ·dV, więc
Praca wykonana przez wypadkową siłę F działającą na ciało jest równa jest zmianie energii kinetycznej tego ciała: W = EK-EK0
świat
ło + ciepło + energia ruchu + energia pola elektrycznego =constans
Energię czegoś można zwiększyć wykonując nad tym pracę!!
Energię kinetyczną mają ciała będące w ruchu. Jej wartość zależy od wyboru układu odniesienia. Energię kinetyczną można obliczyć ze wzoru
![]()
m -masa ciała
V -prędkość z jaką się ono porusza
Energia kinetyczna jest równa pracy jaką trzeba wykonać, aby ciało spoczywające wprowadzić w ruch lub ciało będące w ruchu zatrzymać
Przez energią kinetyczną punktu materialnego rozumiemy energię punktu.
Energia kinetyczna jest wielkością względną i zależy od doboru układu odniesienia
20. Siły zachowawcze i energia potencjalna
Jeśli siła, działając między punktami rA i rB wykona pracę nad ciałem, to praca ta skutkuje wzrostem energii kinetycznej ciała. Ale przed wykonaniem tej pracy, w punkcie rA siła ma potencjalną możliwość wykonania pracy, która maleje wraz z wykonywaniem pracy.
W pewnych warunkach ta pracy jaką potencjalnie może wykonać siła nazywa się energią potencjalną.
W1 - W1
rb rb
ra W2 ra W2
Praca jaką potencjalnie może wykonać siła tylko wtedy tą siłę charakteryzuje, jeśli praca zależy od położenia początkowego i końcowego, a nie od drogi między nimi. Tylko wtedy każdy punkt przestrzeni r w której działa ta siła może mieć przypisaną liczbę: pracę jaką ta siła może wykonać przenosząc ciało od rA do r
Siły są zachowawcze (potencjalne), jeśli praca zależy tylko od punktu początkowego i końcowego, bez względu na drogę, tj. jeśli praca wykonana na drodze zamkniętej jest zero.
Tylko wtedy można określić energię potencjalną
Jak obliczać energię potencjalną
Energia potencjalna to praca siły zachowawczej jaką ta siła może wykonać przenosząc ciało od r0 (przyjęty dowolnie) do r
Sprężyna początkowo rozciągnięta o x od położenia równowagi (punktu standardowego) :
Ruch wzdłuż osi x, pod działaniem siły F(x) = -k x
Przez energię potencjalną punktu materialnego rozumiemy energię, którą ma punkt dzięki jego położeniu
Aby obliczyć energię potencjalną punktu materialnego znajdującego się w polu grawitacyjnym na wysokości h należy obliczyć jaką pracę trzeba wykonać dla podniesienia punktu z powierzchni Ziemi na daną wysokość
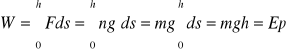
21. Zachowanie energii mechanicznej
Rozpatrujemy ruch ciała z punktu A do punktu B. Gdy jedyną siłą działającą na ciało jest siła zachowawcza to wiemy, że
W = ΔEk = EkB + EkA
W = -ΔEp = -(EpB - EpA)
Korzystając z tych zależności otrzymujemy
-(EpB - EpA) = EkB + EkA lub EkA + EpA = EkB + EpB
Równanie to jest przejawem zasady zachowania energii mechanicznej.
Zasada zachowania energii mechanicznej mówi, że dla ciała podlegającego działaniu siły zachowawczej, suma energii kinetycznej i potencjalnej jest stała.
Jeżeli oprócz siły zachowawczej FZ działa jeszcze siła niezachowawcza FNZ(np. tarcie)
to z twierdzenia o pracy i energii otrzymujemy
WZ + WNZ = ΔEk
a ponieważ WZ = -ΔEp to
WNZ = ΔEk + ΔEp
Widzimy, że siła tarcia zmienia energię mechaniczną układu (zmniejsza ją bo tarcie jest siłą rozpraszającą), zostaje ona przekształcona na energię wewnętrzną ΔEwew, która objawia się wzrostem temperatury ciała i otoczenia. Zmiana energii wewnętrznej jest równa rozproszonej energii mechanicznej.
ΔEk + ΔEp + ΔEwew = 0
Z równania wynika, że energia całkowita, tj. suma energii kinetycznej, energii potencjalnej i energii wewnętrznej nie zmienia się. Mamy więc zasadę zachowania energii całkowitej. Inaczej mówiąc energia może przekształcona z jednej formy w inną, ale nie może być wytwarzana ani niszczona; energia całkowita jest wielkością stałą.
22. Zasada zachowania pędu; wyprowadzić zas. zach. pędu dla dwóch zderzających się kulek
II zasada dynamiki Newtona dla układu punktów materialnych przyjmuje postać
![]()
Przypuśćmy, że suma sił zewnętrznych działających na układ jest równa zeru, wtedy:
![]()
Ten warunek wyraża zasadę zachowania pędu.
Jeżeli wypadkowa sił zewnętrznych działających na układ jest równa zeru, to całkowity wektor pędu układu pozostaje stały.
W każdej chwili cząstka 2 oddziałuje na cząstkę 1 siłą F1, a cząstka 1 oddziałuje na cząstkę siłą F2. Zmiana pędu cząstki 1 pod wpływem zderzenia wynosi
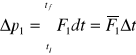
Zmiana pędu cząstki 2 w wyniku zderzenia wynosi
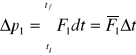
Z prawa Newtona, w każdej chwili F1 = -F2, zatem:
![]()
Jeżeli rozważymy dwie cząstki jako układ odosobniony, to całkowity pęd układu wynosi
P = p1 + p2
a całkowita zmiana pędu układu w wyniku zderzenia równa się zeru, czyli
![]()
Jeżeli nie występują siły zewnętrzne, to całkowity pęd układu nie ulega zmianie podczas zderzenia. Siły impulsowe działające podczas zderzenia są siłami wewnętrznymi, które nie mają wpływu na całkowity pęd układu.
Siły grawitacji np. i siły tarcia też oddziałują na te ciała; wszystkie te siły zewnętrzne nie muszą być takie same i niekoniecznie musza się nawzajem znosić. Jeżeli nawet działają one na układ, to wygodniej jest je pominąć podczas zderzenia i przyjąć, że pęd jest zachowany. Jest to na ogół zgodne z rzeczywistością ponieważ siły zewnętrzne sa bardzo małe w porównaniu z impulsowymi siłami zderzenia.
23. Zasada zachowania momentu pędu; wypowiedzieć i wyprowadzić 2 prawo Keplera
Stosunek zmiany całkowitego momentu pędu układu punktów materialnych względem punktu związanego z inercjalnym układem odniesienia (albo względem środka masy) do czasu, w którym ta zmiana nastąpiła, jest równy sumie momentów sił zewnętrznych działających na ten układ, to znaczy
![]()
Jeżeli suma momentów sił zewnętrznych τzew = 0, to dL/dt = 0, zatem L jest wektorem stałym.
Jeśli wypadkowy moment sił zewnętrznych działających na układ wynosi zero, całkowity moment pędu układu pozostaje stały. Jest to zasada zachowania momentu pedu.
Jeśli wypadkowy moment sił zewnętrznych działających na układ wynosi zero, to
L = const = L0
Jeżeli układem punktów materialnych jest ciało sztywne, obracające się dokoła pewnej osi (np. osi z), która jest nieruchoma w inercjalnym układzie odniesienia, to możemy napisać, że
Lz = Iω
Zasada zachowania momentu pędu w tym przypadku daje się wyrazić w postaci:
Iω = I0ω0 = const
II prawo Keplera (prawo równych pól)
linia łącząca Słońce i planetę zakreśla równe pola w równych odstępach czasu.
prędkość polowa ![]()
24. Wyjaśnić zjawisko precesji
Bąk wiruje dookoła pewnej osi symetrii. Punkt podparcia bąka znajduje się w początku inercjalnego układu odniesienia. Z doświadczenia wiemy, że oś wirującego bąka porusza się dookoła osi pionowej, zakreślając powierzchnie stożka. Taki ruch nazywamy precesją.
Na rysunku bąk ma prędkość kątową ω dookoła swej osi. Ma również moment pędu L względem tej osi,
która tworzy kąt θ z osią pionową.
Wyrażenie wiążące prędkość kątową precesji z momentem siły i momentem pędu ma postać
τ = ωp x L
Zjawisko precesji momentu magnetycznego jest podstawą różnych technik doświadczalnych jak np. magnetyczny rezonans jądrowy (NMR), które znalazły szerokie zastosowanie w badaniach naukowych, technice i medycynie.
25. Zasada względności i jej konsekwencje
Mechanika klasyczna oparta na zasadach dynamiki Newtona poprawnie opisuje zjawiska, w których prędkości ciał są małe w porównaniu z prędkością światła. Jednak w zjawiskach atomowych, jądrowych i w astrofizyce spotykamy się z prędkościami zbliżonymi do prędkości światła i wtedy zamiast mechaniki klasycznej musimy stosować mechanikę relatywistyczną opartą na szczególnej teorii względności opracowanej przez Einsteina. Mechanika klasyczna nie jest sprzeczna z mechaniką relatywistyczną, a stanowi jej szczególny przypadek (dla małych prędkości).
Sformułowana w 1905 r. Szczególna Teoria Względności (STW) wyróżnia pewną klasę układów odniesienia - układy inercjalne. Zgodnie z zasadą względności wszystkie inercjalne układy odniesienia (IUO) są równoprawne a podstawowe równania fizyki są niezmiennicze względem transformacji z jednego układu inercjalnego do drugiego - czyli względem transformacji Lorentza
Obecność innych mas we wszechświecie powoduje, że można odróżniać układy inercjalne od nieinercjalnych poprzez występowanie w tych ostatnich sił bezwładnościowych Dotychczas w klasycznym ujęciu mechaniki związek pomiędzy ruchem jakiejś cząstki a istnieniem innych mas we wszechświecie był całkowicie ignorowany.
Siły bezwładnościowe powstające w NUO mają tę własność, że wszystkim ciałom - bez względu na ich masę - nadają jednakowe przyspieszenie równe co do wartości przyspieszeniu NUO. Zauważmy, że identyczną własność mają siły grawitacyjne. Wiemy, że np. przyspieszenie ziemskie, g, jest jednakowe dla wszystkich ciał na Ziemi. To spostrzeżenie pozwoliło Einsteinowi sformułować zasadę równoważności. Brzmi ona: nieinercjalny układ odniesienia o przyspieszeniu `a' będący poza polem grawitacyjnym jest równoważny (nieodróżnialny) układowi inercjalnemu w polu grawitacyjnym o przyspieszeniu |g| = |a|.
Inaczej mówiąc - „sztuczna grawitacja” powstająca NUO jest nieodróżnialna od grawitacji „prawdziwej” powstającej wokół mas.
Konsekwencje STW:
- wszystkie prawa przyrody są takie same bez względu na to, czy obserwujemy je z układu w spoczynku, czy z układu inercjalnego. Konsekwencją tego jest, że prędkość światła c jest w każdym układzie.
- czas między dwoma zdarzeniami obserwowanymi w układzie nieruchomym jest krótszy niż w układzie ruchomym.
- przedmioty w kierunku ruchu są krótsze w układzie w którym przedmiot się porusza
- masa jest równoważna energii E=mc2
- czas i przestrzeń są nierozłączne: żyjemy w przestrzeni 4 wymiarowej
26. Zegar świetlny: udowodnić, że stałość prędkości światła wymaga, by czas płynął inaczej w różnych układach odniesienia.
Można udowodnić iż z prostego zastosowania postulatów teorii względności wynika, że czas upływa niejednakowo w różnych układach. Zastosować można zasadę niezmienniczości prędkości światła oraz zasadę względności do pomiaru czasu za pomocą prostego zegara zwanego "zegarem świetlnym". Zegarem takim może być rura o ustalonej długości d zamknięta dwoma równoległymi doskonale odbijającymi zwierciadłami, do której wpuszczono krótki impuls świetlny przebiegający rurę w jedną i drugą stronę. Odcinki czasu przebiegu światła wzdłuż rury są jednakowe, czyli takie urządzenie można uważać za zegar. Będziemy teraz za pomocą takich zegarów porównywać przebieg czasu upływającego w dwóch układach - w "nieruchomym" U i "ruchomym" U'. Zgodnie z tym co powiedzieliśmy wyżej, pomiaru chwil czasu dla poszczególnych zdarzeń możemy dokonywać tylko na zegarach znajdujących się w bezpośrednim sąsiedztwie tych zdarzeń. Nie można zatem porównywać czasu jednego zegara spoczywającego w układzie U z jednym zegarem ruchomym, ponieważ kolejne wskazania czasu zegara ruchomego odbywają się w różnych miejscach w układzie U. Dla porównania czasów w obu układach należy w układzie U rozmieścić wiele zsynchronizowanych ze sobą zegarów, które będzie mijał zegar ruchomy. Rysunek przedstawia sytuację, gdzie w miejscach 1 - 5 rozmieszczono identyczne zegary.
W każdym z tych miejsc sygnał bądź to startuje od lustra dolnego (miejsca 1, 3 i 5), bądź zawraca przy lustrze górnym (miejsca 2 i 4). Czas przebiegu światła w jedną stronę w zegarze nieruchomym wynosi to= d/c. Takie odcinki czasu odmierzają kolejno zegary rozmieszczone w punktach 1 do 5. Czas przebiegu światła w identycznym zegarze ruchomym mierzony w układzie U' jest dokładnie taki sam, ponieważ zegar w tym układzie spoczywa i światło ma do przebycia taką samą drogę d z taką samą prędkością, która tu również wynosi c. Natomiast obserwator nieruchomy w układzie U widzi, że światło biegnące w zegarze ruchomym przebywa drogę po przekątnej, czyli dłuższą i musi zużyć więcej czasu na dotarcie do górnego zwierciadła. Na rysunku przedstawiona jest sytuacja, gdzie droga s jest dwukrotnie większa od d (gdy kąt α= 30o, to s = d/sin α =2d). W tym przypadku zdarzenie 2 - chwila dotarcia sygnału do górnego lustra w zegarze nieruchomym występuje wtedy, gdy światło w zegarze ruchomym znajduje się w połowie drogi od dolnego do górnego zwierciadła. Światło w zegarze ruchomym dociera do górnego zwierciadła dopiero w miejscu 3. Widzimy, że zegar ruchomy spóźnia się w stosunku do mijanych kolejno zegarów nieruchomych. To opóźnienie nazywamy spowolnieniem czasu lub dylatacją czasu.Wystarczy obliczyć, o ile spóźni się zegar poruszający się z dowolną stałą prędkością u. Czas przelotu światła po drodze s oznaczymy przez t, zatem
s = c t.
Z drugiej strony, stosując twierdzenie Pitagorasa mamy, że s2 = d2 + l2, gdzie l jest drogą jaką przebywa zegar ze stałą prędkością u w czasie t, l=u t,. a d = c to, zatem
s2 = (c to)2 + (u t)2 ,
lub
(ct)2 = (c to)2 + (u t)2 .
Stąd
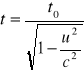
Ponieważ mianownik w tym wzorze jest mniejszy od jedności, więc t > to, czyli według obserwatora nieruchomego czas trwania ruchomego zjawiska jest dłuższy niż tego samego zjawiska ale odbywającego się w ruchomym układzie odniesienia. Czas to nazywa się czasem własnym. Jest to czas trwania zjawiska zachodzącego w pewnym punkcie spoczywającym względem obserwatora. Mimo że dylatację czasu wykazaliśmy tutaj dla specjalnego typu zegarów świetlnych, to można udowodnić, że efekt ten występuje dla wszystkich zjawisk. Istotę tego efektu można wyrazić następująco: Czas trwania jakiegoś zjawiska zachodzącego w pewnym punkcie jest najkrótszy w układzie, względem którego punkt ten spoczywa.
27. Stałość przedziału czasoprzestrzennego i analogia z odległością.
Wyobraźmy sobie pręt o dł. np. .20m. umieszczony w układzie współrzędnych w taki sposób, że rzut tego odcinka na oś x wynosi Δx, a na oś y Δy. Jeśli teraz ktoś znajdzie się w drugim układzie współrzędnych, obróconym względem pierwszego o kąt α, to spoglądając na ten odcinek z tego układu mierzy jego współrzędne jako Δx' i Δy'. Czy jest to dziwne? Oczywiście nie. Możemy także przetłumaczyć opis w jednym układzie na opis w drugim (znaleźć transformację).
Δx' =Δx cosα + Δy sinα
Δy'=-Δx sinα + Δy cosα
Poszczególne wyniki obserwacji Δx i Δy dla jednego człowieka, oraz, odpowiednio, Δx' i Δy' dla drugiego są różne, lecz suma ich kwadratów tj. długość pręta jest taka sama. Związek między Δx i Δy, a Δx' i Δy' jest dany przez liniową kombinację podobnie jak w transformacji Lorentza. Tylko, że tutaj wiemy, że Δx i Δy to odległości, a tam Δx i Δt to wielkości innego rodzaju.
Szczególna teoria względności dowodzi, że czas jest ściśle powiązany z odległością i naprawdę żyjemy w 4-wymiarowej przestrzeni; czasoprzestrzeni. Co więcej, podobna wielkość jak odległość w naszym przykładzie też istnieje: jest nią przedział czasoprzestrzenny (Δx)2-(cΔt)2, który jest niezmiennikiem transformacji Lorenzta, czyli jest taki sam w dwóch układach
(Δx)2-(cΔt)2=(Δx')2-(cΔt')2
28. W rakiecie poruszającej się z prędkością V, wzdłuż osi x' leży pręt o długości L'. Jaką długość tego pręta zaobserwuje obserwator w układzie nieruchomym?
Pomiar dugości pręta polega na zarejestrowaniu dwóch zjawisk zachodzących równocześnie na końcach pręta (np. zapalenie się żarówek). Ponieważ żarówki zapalają się na końcach pręta to Δx' = L'. Ponadto żarówki zapalają się w tym samym czasie (dla obserwatora w układzie spoczywającym ) to dodatkowo Δt = 0. Uwzględniając te warunki otrzymujemy na podstawie transformacji Lorentza
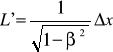
x jest długością pręta L w układzie nieruchomym więc
![]()
Okazuje się, że pręt ma mniejszą dugość, jest krótszy.
28. (drugi przypadek )Teraz rozpatrywany jest przypadek gdy obiekt ma pewną prędkość Ux' w ruchomym układzie odniesienia (tj. względem rakiety). Jaką prędkość Ux zarejestruje nieruchomy obserwator, w układzie którego rakieta porusza się z prędkością V wzdłuż osi x. Z transformacji Lorentza wynika, że
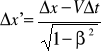
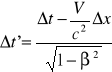
Dzieląc te równania przez siebie otrzymujemy
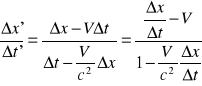
a po podstawieniu![]()
i![]()
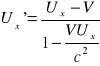
(1)
Równanie (1) można rozwiązać ze względu na Ux
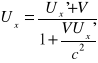
(1b)
W ogólności, jeśli obiekt przesuwa się z prędkością ![]()
, względem obserwatora w rakiecie (poruszającej się z prędkością U wzdłuż osi x) to prędkość ![]()
tego przedmiotu zarejestrowana w nieruchomym układzie wyniesie
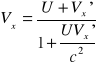
29. Sformułować i wyjaśnić paradoks bliźniąt
W swoje 21 urodziny Jacek zostawia swego brata bliźniaka Placka i udaje się w podróż w kierunku x na 7 lat swego czasu z prędkością 24/25c, poczym zawraca i z taką samą prędkością, podróżując znowu 7 lat spotyka swego brata. W jakim obaj są
Wieku? Rozwiązanie:
Wiek Placka po powrocie: 2·25/7 ·7 +21 lat= 71
Wiek Jacka po powrocie 21+14=35
30. Napisać i omówić transformacje Lorentza. Dowieść ,że dla małych prędkości przechodzi ona w transformację Galileusza.
Transformacja Lorentza. przekształcenie matematyczne opisujące transformacje wielkości fizycznych w czasoprzestrzeni czterowymiarowej przy przechodzeniu od jednego inercjalnego układu odniesienia, określonego przez współrzędne przestrzenne x, y, z i współrzędną czasową t, do drugiego, określonego przez współrzędne x', y', z' oraz t'. W najprostszym przypadku, jeśli układ (x', y', z', t') porusza się jednostajnie w kierunku osi x z prędkością v, to transformacja Lorentza ma postać: gdzie c - prędkość światła w próżni, β = V/c. Transformacja współrzędnych, która uwzględnia niezależność prędkości światła od układu odniesienia ma postać:
Z transformacji Lorentza wynikają wszystkie efekty kinematyczne szczególnej teorii względności, takie jak: reguła sumowania się prędkości prowadząca do niemożności uzyskania prędkości większej od prędkości światła, względność pojęcia równoczesności, skrócenie Lorentza-Fitzgeralda, spowolnienie biegu poruszających się zegarów. Dla małych prędkości v, otrzymuje się klasyczne przekształcenie Galileusza.
Dla małych prędkości: V → 0 [m/s]
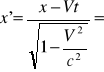
po podstawieniu V mianownik wynosi 1 ⇒ x' = x - Vt
po podstawieniu v mianownik wynosi 1,licznik wynosi t ⇒t'= t
31. Energia i pęd relatywistyczny. Co to jest masa relatywistyczna i masa spoczynkowa. Dla jakiej prędkości masa relatywistyczna ma wartość 2 razy większą niż masa spoczynkowa.
Pęd relatywistyczny:
W mechanice relatywistycznej , tak jak w klasycznej ,pęd p punktu materialnego jest proporcjonalny do masy i pokrywa się co do kierunku i zwrotu z prędkością V tego punktu. Jednakże w odróżnieniu od mechaniki Newtonowskiej , punkt punktu materialnego jest nieliniową funkcją jego prędkości: 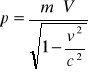
. Jeżeli V<<c(dokładniej, w granicy, gdy c → 0),to wyrażenie dla pędu jest takie samo jak przyjęte w mechanice klasycznej p=m⋅V. Wielkość m nazywamy masą spoczynkową punktu materialnego ,
a 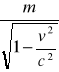
jego masą relatywistyczną.
Energia relatywistyczna:
W przypadku ogólnym zmiana energii całkowitej W ciała jest związana z jego masą i prędkością następującą zależnością:
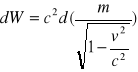
spełniony jest zatem związek masy i energii:
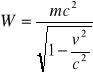
W mechanice relatywistycznej, podobnie jak w fizyce klasycznej, spełniona jest zasada zachowania energii: energia całkowita układu izolowanego nie zmienia się w czasie.
-Przyrost energii kinetycznej Wk punktu materialnego = pracy, wykonanej przez działającą na ten punkt siłę F.
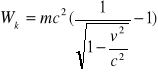
gdzie m jest masą punktu. Rozwijając (1-v2/c2) w szereg Maclaurina ,otrzymujemy:
Wk=mc2[0,5(v/c)2+3/8(v/c)4+..]
Dla v<<c wzór ten prowadzi do zwykłego wyrażenia na energię kinetyczną , stosowany w mechanice klasycznej Wk=0,5mv2
-Energia całkowita będącej w stanie spoczynku cząstki lub układu cząstek
(na przykład jądra atomowego, atomu, cząsteczki, ciała ) równą Wo=mc2 nazywamy energią spoczynkową cząstki lub układu.
Masa relatywistyczna osiągnie wartość 2 razy większą od masy spoczynkowej gdy prędkość v wynosi w przybliżeniu v = 260'000 [km/s]
czyli osiąga ok 86,6% prędkości światła.
32. Zasady powstawania i kontroli obrazu w monitorze klasycznym.(tłumaczenie z angielskiego)
Obraz na ekranie telewizyjnym jest zbiorem wielu punktów świetlnych. Nie wszystkie punkty są pokazane jednocześnie, zaświecją się po kolei rzędami.
Jeżeli następuje to wystarczająco szybko, człowiekowi zdaje się, że punkty zaświecają się jednocześnie. Wyświetlane punkty są jaśniejsze ,bądź ciemniejsze . W ten sposób otrzymujemy obraz na ekranie.
Zasada : w telewizorze znajduje się lampa katodowa. Katoda jest ujemnie naładowaną płytką , która jest podgrzewana tak ,by dostarczyć energię pozwalającą na emisję elektronów. Te elektrony zostają przyspieszane ku dodatnio naładowanej anodzie. Elektrony opuszczają anodę i biegną w przypadkowych kierunkach dopóki nie miną obszaru między katodą i anodą. Pole elektryczne znajdujące się między katodą i anodą formuje je w promień. Promień pola pada na wewnętrzną stronę ekranu , która jest pokryta plamkami fosforu, który jarzy się , kiedy zostaje uderzona przez elektron. W miarę jak elektrony uderzają w ekran , plamki fosforu zaświecają się . Tak powstaje punkty na ekranie.
Po wyświetleniu jednego obrazu promień elektronu biegnie od nowa po ekranie tworząc drugi obraz, różniący się od poprzedniego. Zmieniające się szybko obrazy z powodu bezwładności wzroku dają wrażenie ruchu.
Punkty świetlne mogą być jaśniejsze lub ciemniejsze w zależności od intensywności promieniowania elektronów . Im więcej elektronów uderza w pokryty fosforem ekran w jednostce czasu ,tym jaśniejszy obraz otrzymujemy . Reguluje się to poprzez zmianę napięcia między anodą a katodą. Strumień elektronów jest odchylany poprzez elektromagnesy w poziomie i pionie, kierując go w pożądane miejsce na ekranie.
Kolory: jak wiadomo poszczególne kolory otrzymuje się poprzez nakładanie na siebie kolorów podstawowych oraz rozjaśnianie i przyciemnianie ich.
W telewizorze jest trochę inaczej : poszczególne kolory składające się na światło białe (tj czerwony, zielony i niebieski ) są odbijane lub absorbowane , odbite składniki są następnie łączone/nakładane. Np.: żółta powierzchnia absorbuje światło niebieskie , a odbija czerwone i zielone. W telewizorze istnieją 3 strumienie elektronów i 3 typy plamek fosforowych. Każdy ze strumieni elektronów jest kierowany przez siatkę tak, by wylądować na plamkę odpowiedniego koloru. W ten sposób otrzymujemy 3 podstawowe kolory. Regulując intensywności każdego z nich można uzyskać każdy
kolor. Z daleka 3 plamki o różnych kolorach wyglądają jak jedna o kolorze wypadkowym.
33. Co to jest polaryzacja światła; w jaki sposób światło można spolaryzować.
W powszechnie stosowanych źródłach światła fale świetlne są promieniowane przez poszczególne atomy lub cząsteczki, w postaci sygnałów, zwanych również ciągami falowymi. W każdym ciągu falowym zachowane jest stałe położenie płaszczyzny drgań wektora elektrycznego . W świetle promieniowanym przez ciało składające się z atomów lub cząsteczek mamy wiele niezależnych od siebie ciągów falowych, których płaszczyzny drgań wektora elektrycznego są różnie zorientowane w przestrzeni. Zatem fala świetlna wypromieniowana przez źródło światła jest niespolaryzowana.
E b) E
a)
Rys. a -drgania wektora elektrycznego E fali świetlnej niespolaryzowanej, zwanej również światłem naturalnym, rozchodzącej się prostopadle do płaszczyzny rysunku.
Rys. b -drgania wektora elektrycznego fali świetlnej o ściśle określonej płaszczyźnie drgań, czyli spolaryzowanej liniowo. Nazywamy ją również falą płasko spolaryzowaną. Światło naturalne ulega polaryzacji podczas odbicia od ośrodków dielektrycznych, na przykład szkła. Gdy na płytkę szklaną skierujemy wiązkę światła naturalnego, wówczas część jej odbije się, a pozostała część przechodzi przez płytkę. Fala świetlna odbita jest częściowo lub całkowicie spolaryzowana. S
E
90o
E
Fala ulega całkowitej polaryzacji przy odbiciu od granicy dielektrycznego ośrodka przezroczystego, gdy promienie odbity i załamany tworzą kąt 90o (prawo Brewestera). Płaszczyzna drgań wektora elektrycznego E , zwanego wektorem świetlnym, w fali odbitej jest prostopadła do płaszczyzny padania. Odbiciu ulega ta część fali, której drgania wektora świetlnego są prostopadłe do płaszczyzny padania. Fakt ten można wykorzystać do rozpoznania, czy fala jest spolaryzowana czy też nie.
Gdy na kryształ szpatu islandzkiego prostopadle do jego ściany, skierujemy wiązkę światła, dzieli się ono na dwie części. Jedna z nich spełnia prawo załamania światła, druga natomiast nie spełnia tego prawa. Dlatego zwiemy je odpowiednio wiązką zwyczajną i nadzwyczajną. Za pomocą analizatora można stwierdzić, że obie wiązki są spolaryzowane w płaszczyznach wzajemnie prostopadłych. Wydzielając jedną z nich otrzymamy falę świetlną spolaryzowaną.
Podwójne załamanie światła
w węglanie wapniowym l- oś optyczna
Promień nadzwyczajny
Promień zwyczajny
Spotykamy kryształy, które silnie pochłaniają jedną z tych wiązek. Kryształ turmalinu już przy grubości kilku milimetrów prawie całkowicie pochłania wiązkę zwyczajną. Z kryształu tego wychodzi spolaryzowana wiązka nadzwyczajna. Na podobnej zasadzie jak polaryzator z turmalinu działają płytki wykonane sztucznie, zwane polaroidami. Na przezroczystą błonę nakłada się warstwę drobnych kryształków organicznych jednakowo zorientowanych. Warstwę tę, w celu ochrony, pokrywa się drugą warstwa przezroczystą.
34. Ciekłe kryształy i ich wykorzystanie w konstrukcji wyświetlaczy
Cechą charakterystyczną struktury kryształów jest określone uporządkowanie atomów lub cząsteczek. Związana jest z tym anizotropia ich różnych właściwości fizycznych, mechanicznych optycznych, elektrycznych, magnetycznych i wielu innych. Okazuje się że takimi właściwościami wyróżniają się nie tylko ciała stałe, lecz również w określonych warunkach niektóre ciecze.
Po raz pierwszy optyczne właściwości anizotropowe cieczy zostały zaobserwowane w 1888r. przez F. Reinitzera, w 1889r. zaś O. Lehmann stwierdził, że ciecz taka jest odmiennym stanem materii, którą nazwał ciekłym kryształem. F. Reinitzer pierwszy zsyntezował benzoesan cholesterylu i określając różne jego właściwości fizyczne swierdził, że przy pomiarze temperatury topnienia zachowuje się on wyjątkowo nietypowo.
W temperaturze 145,4oC białe kryształy benzoesanu topiły się , tworząc mętną białą ciecz, która przy podgrzaniu do temperatury 178,5oC stawała się nagle przeźroczysta. W procesie stygnięcia te same zjawiska zachodzą identycznie , lecz w odwrotnej kolejności . Stan przejściowy między ciałem stałym a klarowną cieczą nazywamy fazą mezomorficzną (mezofazą) , gdyż mętna ciecz jest fazą pośrednią. Badanie optyczne mezofazy tego związku pozwoliły stwierdzić , że powstaje w niej zjawisko podwójnego załamania światła takie samo, jakie jest obserwowane w niektórych kryształach stałych. Na tej podstawie O. Lehmann mezofazę benzoesanu cholesterylu nazwał ciekłym kryształem i stąd tę nazwę rozciągnięto na cały zbiór ciekłokrystalicznych związków. Obecnie znamy około 60 tys. różnych ciekłych kryształów. Ciekłe kryształy można otrzymywać dwoma sposobami: po stopnieniu odpowiednich substancji kryształów stałych lub też po rozpuszczeniu innych substancji w odpowiednim dla nich rozpuszczalniku. Wszystkie ciekłe kryształy wyróżniają się tym, że mierzona dowolnie wybrana ich własność fizyczna przyjmuje różne wartości w różnych kierunkach względem wybranej osi. Własność taką nazywamy anizotropią. Ciekłe kryształy wykazują anizotropię optyczną, elektryczną magnetyczną, lepkości, przewodnictwa elektrycznego i cieplnego i innych wielkości. Ze wzrostem temperatury wszystkie ciekłe kryształy tracą swoje własności anizotropowe i stają się zwykłą cieczą. Zjawisko takie tłumaczymy ruchami termicznymi cząsteczek, które rosną ze wzrostem temperatury co powoduje niszczenie struktur odpowiednio uporządkowanych cząsteczek. Oznacza to, że w ciekłych kryształach zawsze występuje określone uporządkowanie cząsteczek ciekłego ośrodka. Obecnie ze względu na rodzaj struktury ciekłe kryształy dzielimy na dwa typy: nematyki i smektyki oraz ich pochodne chiralne: nematyki chiralne i smektyki chiralne. Cząsteczki tworzące kryształy nematyczne mają kształt bardzo wydłużony, ich długość jest około 10 razy większa od ich szerokości, układają się one równolegle względem siebie. Nazwa nematyk pochodzi od greckiego słowa nić. W kryształach smektycznych cząsteczki równoległe względem siebie są rozmieszczone warstwami. Osie długie tych cząsteczek są prostopadłe lub nieco nachylone względem tych warstw. Nazwa smektyk pochodzi od greckiego słowa smegma - mydło. Mętność i lepkość smektyków jest podobna do stężonych roztworów mydlanych. Niektóre substancje odznaczają się polimorfizmem, to znaczy , że mają więcej niż jedną fazę ciekłokrystaliczną. Niekiedy ta sama ciecz występuje w niższych temperaturach jako smektyczna, a przy podwyższeniu temperatury przechodzi w fazę nematyczną. Po stopieniu substancji polimorficznej najpierw występuje smektyk lub kilka odmian smektyka, a na końcu nematyk. Przy chłodzeniu kolejność występowania faz jest odwrotna. Ponieważ ciecze nie mają sprężystości kształtu dzięki temu ciekłe kryształy przyjmują dowolny kształt przestrzeni, którą wypełniają, a zatem można dowolnie kształtować ich wymiary geometryczne. Umożliwia to budowanie wyświetlaczy dowolnego kształtu do zegarków elektronicznych , kalkulatorów, ekranów radarowych i innych.
35. Masa atomowa pierwiastka; od czego zależy masa atomowa
Symbol pierwiastka nie tylko przedstawia jakościowo atom danego pierwiastka , lecz uwzględnia także jego masę. Najlżejszy jest atom wodoru i z tego powodu próbowano obrać masę atomu wodoru za jednostkę mas innych atomów. Okazało się jednak, że korzystniejsze jest wzięcie za podstawę obliczeń tlenu, przyjmując dla jego atomu masę równą 16 umownych jednostkom masy atomowej.
Gdy ustalono przyjęcie atomu tlenu za podstawę oznaczenia mas atomowych nie wiedziano, że tylko 99,757% tych atomów ma masę 16. Obok nich w tlenie jest 0,039% atomów cięższych o masie 17 i 0,204% atomów o masie 18. Mówimy, że tlen w przyrodzie jest mieszaniną trzech izotopów. Węgiel ma dwa izotopy : 12C i 13C. Średnia masa atomowa węgla w skali tlenowej wynosi 12,011. W 1962 r. zawarto międzynarodową umowę, w myśl której za jednostkę masy atomowej przyjęto 1/12 część masy atomu lżejszego izotopu węgla. Według tej skali atom lżejszego izotopu węgla ma masę dwunastu umownych jednostek atomowych.
Masę atomowa danego pierwiastka nazywamy liczbę, która podaje średnią masę atomu wyrażoną w jednostkach umownych.
Izotop węgla 12C6 przyjęty jest za jednostkę masy atomowej ≡ masa atomowa 12
![]()
A-liczba masowa = ile razy masa atomu pierwiastka jest większa od 1/12 masy węgla 12C6 (w przybliżeniu suma protonów i neutronów )
Z-liczba atomowa = liczna protonów
Izotopy są to pierwiastki o tej samej liczbie protonów (głównie decydującej o własnościach), lecz o różnej licznie neutronów.
Masa atomowa zależy od położenia w układzie okresowym danego pierwiastka.
Rzędy: wzrastająca masa atomowa
Początkowe lata 1800: chemicy (John Dalton) dowodzą, że masy pierwiastków w reakcjach chemicznych muszą być w ściśle określonych proporcjach. (np. w przypadku reakcji tlenu i wodoru prowadzącej do wody stosunek masy tlenu i wodoru był zawsze 8: jeden atom tlenu waży tyle co 16 atomów wodoru)
36. Co to jest funkcja falowa; jaka jest jej interpretacja i jak się ją oblicza? Jakie liczby kwantowe określają funkcję falową dla atomu wodoru.
Elektron (i inne cząstki mikroświata) zachowują się dziwnie
X ilość elektronów
nie patrzymy → interferencja
patrzymy → brak interferencji
konieczność innego opisu
Funkcja falowa (amplituda prawdopodobieństwa)
<xIψ>≡ψ(x)- amplituda prawdopodob. (funkcja falowa) że elektron w stanie Iψ> znajdziemy na ekranie w x
<1Iψ>: amplituda prawdopodob. że elektron w stanie Iψ> znajdziemy przy szczelinie 1
Zasada nieoznaczoności:
albo interferencja, albo wiedza przez którą szczelinę przeszedł elektron; obu naraz mieć nie
możemy
Interpretacja funkcji falowej
Iψs(x)I2 - prawdopodobieństwo, że elektron w stanie Iψ> znajdziemy na ekranie w miejscu x
I<1Iψ>I2 : prawdopodobieństwo, że elektron w stanie Iψ> znajdziemy przy szczelinie 1
Obliczanie funkcji falowej ψ(x) za pomocą równania Schrödingera niezależnego od czasu
funkcja falowa ψ(x) dozwolone energie
Hamiltonian H niesie całą informację o warunkach w których znajduje się elektron
Dla atomu wodoru funkcję falową określają trzy liczby kwantowe:
-magnetyczna liczba kwantowa ml=0,±1,±2,....
-orbitalna liczba kwantowa l ≥| ml|
-główna liczba kwantowa n= l+1,l+2,l+3,.....
37. Model Bohra atomu wodoru.
Badanie widma wodoru doprowadziło Nielsa Bohra do sformułowania postulatu, że kołowe orbity elektronów są skwantowane tj. że ich moment pędu może mieć wartość równą wyłącznie którejś z całkowitych wielokrotności pewnej podstawowej wartości. Ilustruje on ideę kwantowania w prostszym matematycznie obszarze fizyki klasycznej.
Bohr założył że atom wodoru, podobnie jak oscylatory Plancka, może znajdować się jedynie w pewnych ściśle określonych stanach stacjonarnych w których nie wypromieniowuje energii. Wypromieniowanie następuje tylko gdy atom przechodzi z jednego stanu Ek do stanu o niższej energii Ej . ![]()
![]()
- kwant energii uniesionej przez foton wypromieniowany z atomu w czasie przejścia.
Załóżmy że elektron w atomie wodoru porusza się po kołowych orbitach o promieniu r ze środkiem w miejscu jądra, zakładamy że jądro które jest pojedynczym protonem jest tak ciężkie że środek masy układu pokrywa się ze środkiem protonu.
Z 2 zasady dynamiki dla ruchu elektronu i prawa Coulomba : F = m*a lub
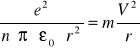
energia kinetyczna elektronu 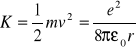
energia potencjalna ukł. proton - elektron 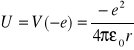
,![]()
V - potencjał pola wytworzonego przez proton w odległości równej promieniowi orbity elektronu.
Energia całkowita 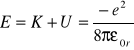
Jeżeli dany jest promień orbity, określone są wszystkie własności orbit.
Prędkość liniowa elektronu 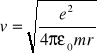
Częstość obrotów 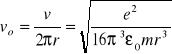
Pęd 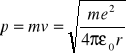
Moment pędu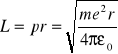
Jeżeli któraś z wielkości jest skwantowana to pozostałe są skwantowane.
Bohr założył że kwantyzacja parametrów jest najprostszą jeżeli zastosujemy ją do momentu pędu L, który może przyjmować wartości ![]()
, h - stała Plancka, n - liczba kwantowa.
Na podstawie wzorów na moment pędu: ![]()
,
więc energia 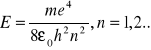
Z równania tego otrzymujemy bezpośrednio wartości energii dozwolonych stanów stacjonarnych.
Teoretyczny wzór dla częstości linii widmowych wodoru:
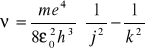
k,j - liczby całkowite opisujące niższy i wyższy stan stacjonarny.
38. Stany energetyczne wg Bohra i wg modelu kwantowo - mechanicznego.
I.wg Bohra:
Ze wzoru na energię całkowitą elektronu 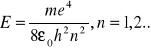
widać że kwantowanie orbitalnego momentu pędu elektronu prowadzi do kwantowania jego energii całkowitej.
Informacje zawarte w równaniu na energię przedstawia się w postaci wykresów poziomów energetycznych.
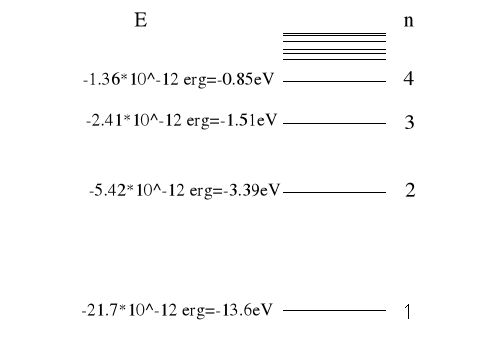
Energia poziomów podana w elektronowoltach. Najniższa (najbardziej ujemna) dozwolona wartość energii całkowitejwypada dla liczby kwantowej n=1.
II.w teorii mechaniki kwantowej (wg Schrodingera)
Wzór na dozwolone wartości energii stanów związanych atomu: 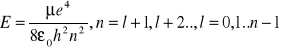
![]()
![]()
- masa zredukowana elektronu, m- masa elektronu, M- masa jądra.
Porównując ten wzór z przewidywaniami modelu Bohra, widzimy że obie teorie przewidują identyczne dozwolone energie. Wartości te doskonale zgadzają się z wynikami doświadczeń.
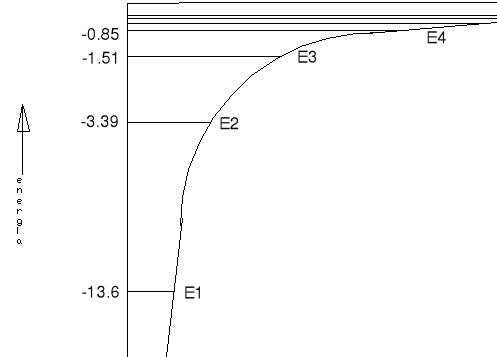
39. Stany energetyczne atomów o wyższych liczbach Z.
Atom wieloelektronowy o liczbie atomowej Z składa się z jądra o ładunku +Ze otoczonego Z elektronami, z których każdy ma ładunek -e. Każdy elektron porusza się pod wpływem przyciągającego oddziaływania kulombowskiego jądra i odpychającego oddziaływania wszystkich pozostałych Z-1 elektronów oraz pewnych słabszych odddziaływań związanych z momentami pędu.
Zakaz Pauliego: W atomie wieloelektronowym w tym samym stanie kwantowym może znajdować się co najwyżej jeden elektron.
Teoria Hartreego: wszystkie elektrony powłoki n atomu wieloelektronowego poruszają się w potencjale kulombowskim.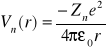
, Zn-stała równa wartości Z® dla średniej wartości r powłoki.
Postulaty Teorii Hartreego:
1: w atomach wieloelektronowych wewnętrzne powłoki o małych n mają bardzo małe promienie, gdyż ekranowanie tych powłok jest słabe i na ich elektrony działa pełne przyciąganie kulombowskie jąder o dużym ładunku.
2: elektrony powłok wewnętrznych znajdują się w obszarze o dużej ujemnej energii potencjalnej, tak więc ich energie całkowite są duże i ujemne.
3: elektrony zewnętrznych powłok o dużym n są prawie całkowicie ekranowane od jądra.
4: Całkowita energia elektronu w najbardziej zewnętrznej wypełnionej powłoce dowolnego atomu jest porównywalna z energią elektronu w stanie podstawowym atomu wodoru.
5: całkowita energia elektronu w atomie wieloelektronowym szybko rośnie ze wzrostem n dla małych n. Dla dużych n wzrost jest wolniejszy.
Z=2 (hel) Jon helu He+ mający tylko jeden elektron musi mieć te same poziomy energii co wodór, tylko cztery razy wyższe.
Z=3 (lit) Podwójnie zjonozowany lit Li++ będzie miał widmo podobne do atomu wodoru, w którym poziomy energetyczne będą dziewięć razy wyższe od poziomów energetycznych wodoru.
Z=4 (beryl) W stanie n=2 mogą znajdować się dwa elektrony (zakaz Pauliego).
dx
-
-
-
-
-
-
+
+
+
+
+
+
+
F1
F2
m1
m2
S
r
r
rϕ
ϕ
ΔL
θ
L
z
y
x
τ
L+ΔL
Δϕ
ωp
z
y
x
τ
L
mg
θ
r
![]()
V
![]()
V≠0
V=0
całkowita siła F
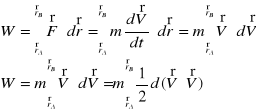
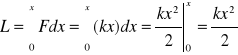

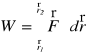
![]()
x
α
B
A
x
y
B
A
A × B
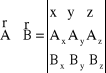
![]()
rA
rB
W2
W2
W1
rB
y
X
X'
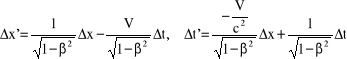
Δx
A
Linia świata Placka
Linia świata Jacka
Δt
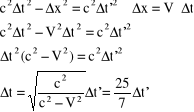
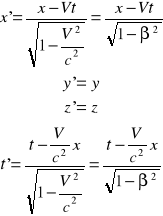
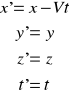
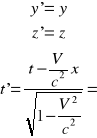
![]()
Wyszukiwarka
Podobne podstrony:
egz fizyka cz 1
odp do egz, fizyka + matma UMK, matematyka, matma
Zag na egz elem fiz wsp-Wolarz-2015, ETI, III Sem, fiza, Fizyka egz, Fizyka egz
egz fizyka cz 2
fizyka II egz Fizyka II, IŚ , grupa 4 , termin I
egz fizyka cz 1 id 151175 Nieznany
fizyka-zagadnienia na egz, fizyka lab
fizyka II egz fizykaaa
Ściągi z egz Fizyka, AGH górnictwo i geologia, II SEM, Fizyka I
egz. fizyka, fizyka + matma UMK
egz fizyka cz 2
fizyka II egz Fizyka II, IŚ, I termin, 9 02 2015, grupa 3
egz fizyka cz 1
fizyka II egz grupa 1
Fizyka zadania, Semestr III, Fiza, egz
Fizykaopracowanie zgadnien-nowe, Semestr III, Fiza, egz
więcej podobnych podstron