KINEMATYKA PUNKTU MATERIALNEGO

Kinematyka bada ruch ciał nie wnikając w przyczyny warunkujące ten ruch.

Ruch: względne przemieszczanie się ciał lub ich części.

Punkt materialny: ciało, którego rozmiary są zaniedbywane, może poruszać się tylko w przestrzeni.

Opis ruchu: 1) Układ odniesienia: tworzy go zbiór nieruchomych względem siebie ciał, służy do rozpatrywania ruchu innych ciał

2) tor: linia zakreślana przez poruszający się punkt materialny. Odległość mierzona między początkiem toru i końcem to droga s.Wektor o początku w początku toru i końcu w punkcie końcowym toru to przemieszczenie r.

3) Prędkość: droga przebywana w jednostce czasu. Jeśli w ciągu równych odstępów czasu punkt przebywa jednakowe drogi to ruch jest jednostajny. W przypadku gdy podzielimy tor na bardzo małe fragmenty o długości ds. to każdemu fragmentowi odpowiada małe przemieszczenie dr. Prędkość jest wektorem stycznym do toru, więc dzielimy to przemieszczenie przez odpowiednio mały odstęp czasu dt i otrzymujemy prędkość chwilową v=dr/dt=r, v=r - prędkość jest więc pochodną położenia punktu materialnego po czasie.

Prędkość średnia: v_śr.=dr/dt.

4) Droga- pochodna v po t (przebyta w czasie t1-t2),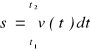
.

Ruch: a)prostoliniowy jednostajny, a=0, v-v_o-const

b)jednostajnie zmienny prostoliniowy a_t=a_o,

c)jednostajny po okręgu

Prędkość kątowa skierowana jest wzdłuż osi obrotu ciała i ma zwrot określony regułą śruby prawoskrętnej. Ruch obrotowy ze stałą prędkością kątową nazywamy jednostajnym. Ruch po okręgu jest zwany ruchem periodycznym

PRZYSPIESZENIE STYCZNE I NORMALNE

Przyspieszenie - jedna z podstawowych, wektorowych wielkości charakteryzujących ruch; a = dv/dt Przyspieszenie styczne występuje w ruchu po okręgu, jest składową o kierunku stycznym do toru, związany jest ze zmianami wartości prędkości w ruchu po okręgu. Całkowita wartość przyśpieszenia chwilowego w ruchu po okręgu jest więc równa a=(a_t²+a_r²)^1/2

a_t - przyspieszenie styczne

a_r - przyspieszenie dośrodkowe, a_r=v²/r (r- promień krzywizny toru)

PRAWA NEWTONA

Zasady dynamiki Newtona

1. Punkt materialny, na który nie działa żadna siła lub działające siły równoważą się, pozostaje w spoczynku lub porusza się ruchem jednostajnym w linii prostej (układ inercjalny).

Układy odniesienia, w których jest spełniona I z.d. Newtona nazywamy układami inercjalnymi. Każdy układ odniesienia, będący w spoczynku lub w ruchu jednostajnym prostoliniowym względem dowolnego układu inercjalnego jest też układem inercjalnym.

Analogicznie: układy nie spełniające I z.d. Newtona to układy nieinercjalne. Jest ich nieskończenie wiele (np. układ związany z hamującym lub przyspieszającym pojazdem, z pojazdem na zakręcie)

2. Jeśli na ciało działają siły nie równoważące się, to porusza się ono ruchem zmiennym, a przyśpieszenie ciała jest wprost proporcjonalne do wypadkowej sił działających na to ciało, a odwrotnie proporcjonalne do masy ciała (klasyczna postać) - przyspieszenie jest skutkiem działania siły na ciało o niezerowej masie

inaczej szybkość zmiany pędu punktu materialnego jest proporcjonalna do działającej wypadkowej siły F

(równanie ruchu)

Wiemy, że
, a w związku z tym, że masa w mechanice newtonowskiej jest stała, możemy zapisać, że

.

Inaczej sformułowana II zasada dynamiki Newtona brzmi: iloczyn masy ciała i przyspieszenia jest równy sile działającej na ciało.

3. Jeśli jedno ciało działa z określoną siłą na drugie (siła akcji), to i wzajemnie drugie ciało działa na pierwsze ciało siłą taką samą co do wartości i kierunku lecz przeciwnie zwróconą (siła reakcji).

A B

(nie równoważą się, bo działają na różne ciała!)

Przykładem mogą być dwie obojętne elektrycznie cząstki
i
, oddalone od siebie o odległość r. Cząstki te, na skutek powszechnego ciążenia, przyciągają się wzajemnie siłami o wartości

(prawo ciążenia)

Prawo powszechnej grawitacji Newtona (prawo powszechnego ciążenia)

Wszystkie ciała obdarzone masą przyciągają się wzajemnie siłami grawitacji. Wartość siły wzajemnego przyciągania się dwóch ciał jest wprost proporcjonalna do iloczynu mas tych punktów, a odwrotnie proporcjonalna do kwadratu odległości między nimi. Wektor siły grawitacji leży na prostej przechodzącej przez środki obu mas.

MOMENT PĘDU

Moment pędu
punktu materialnego P o pędzie
względem punktu 0 jest określony iloczynem wektorowym
 = 
×
, gdzie
— promień wodzący poprowadzony od punktu 0 do P. Moment pędu bryły sztywnej względem osi, wokół której obraca się z prędkością kątową
, wyraża się wzorem
 = I
, gdzie I — moment bezwładności bryły względem tej osi. Moment pędu spełnia zasadę zachowania: moment pędu zamkniętego układu mech., tj. takiego, na który nie działają siły zewnętrzne, pozostaje wielkością stałą; siły wewn. nie mogą zmienić całkowitego momentu pędu układu, choć momenty pędu poszczególnych ciał układu mogą ulec zmianie. Zmianę momentu pędu wywołuje działanie na ciało momentu siły
; zgodnie z drugą zasadą dynamiki ruchu obrotowego: Δ
 = 
Δt.

TRANSFORMACJA GALILEUSZA

Rozważmy dwa układy odniesienia, które poruszają się względem siebie ze stałą prędkością v₀. Układ oznaczony literą K uważamy za nieruchomy. Układ K' porusza się więc wzglądem K ruchem jednostajnym prostoliniowym. Osie układu współrzędnych dobieramy tak, żeby osie x i x' pokrywały się, a pozostałe były do siebie parami równoległe. Załóżmy, że czas zaczęto mierzyć w chwili, w której początki obu układów pokrywały się. Z rysunku wynika, że
. Oczywiste jest przy tym, że
oraz
. W mechanice klasycznej przyjmuje się, że czas płynie tak samo w obu układach:
. Równania na x,y,z,t nazywamy przekształceniami Galileusza. Pierwszy i ostatni związek są słuszne tylko dla v₀<<c. Różniczkując powyższe wzory po czasie otrzymamy związek między prędkościami punktu P w układach K i K':

lub
, oraz
,
lub
,
.

RUCH W UKŁADACH NIEINERCJALNYCH

Układ nieinercjalny to układ odniesienia, którego wektor prędkości zmienia się, czyli taki, który ma niezerowe przyśpieszenie.(Układ nieinercjalny porusza się z pewnym przyśpieszeniem względem układu inercjalnego). Wektor prędkości może zmieniać swoją wartość (ruch przyśpieszony po linii prostej) lub kierunek (ruch po okręgu) . Charakterystyczną cechą układów nieinercjalnych jest występowanie sił pozornych. Siła pozorna jest skierowana zawsze przeciwnie do kierunku przyśpieszenia układu. Siły te są bezźródłowe. W układach nieinercjalnych nie jest spełnione pierwsze prawo Newtona.

Wyróżniamy trzy główne siły pozorne.

-siła bezwładności(siła d'Alamberta) F_b = -ma gdzie a -przyspieszenie układu (siła ta działa tylko w ruchu po lini prostej);

-siła odśrodkowa F_od=mω²r gdzie ω- prędkość kątowa układu(siła działa tylko w ruchu kołowym ,jest skierowana przeciwnie do początku układu);

-siła Coriolisa
(siła działa w postępowym układzie obrotowym siła nie działa gdy wektor v jest równy wektorowi ω);

Ziemia jest w przybliżeniu układem inercjalnym chociaż działają na niej siła odśrodkowa i siła Coriolisa charakterystyczne dla ukł nieinercjalnych. Ich wpływ można jednak zaniedbać.

PRACA I ENERGIA W MECHANICE

Praca - skalarna wielkość fizyczna zdefiniowana jako iloczyn skalarny siły F i przesunięcia s, oraz kątem zawartym miedzy tymi wektorami.

dA=F*ds.=F*cosα*ds

Wykonywana praca wiąże się ze zmiana energii ciała, na które działa siła.

Wektor siły jest zawsze styczny do kształtu powierzchni po której się porusza.

Pracę sił wypadkowych możemy zamienić na przyrost Energii:

L_1,2=E₂-E_1.

Praca jest dodatnia gdy cosα>0, czyli mamy do czynienia z kątem ostrym.

Gdy jest cosα<0 to mamy kąt rozwarty i praca jest ujemna. Gdy cosα=0, czyli α=π/2 praca jest zerowa L=0.

Praca jest skalarem czyli nie jest zależna od układu odniesienia, nie zależy też od toru, ale od położenia początkowego i końcowego wektora.

Praca to pole pod wykresem zależności siły od drogi:

Jednostką jest Jul [J]=[N*m]=[kg*m²/s²]

Energia-skalarna wielkość przydatna w ilościowej analizie procesów i zjawisk fizycznych ze względu na spełnienie prawa zachowania. Przyrost energii to praca.

Energia jest wielkością addytywną , czyli energia dwóch ciał czy układów nie oddziałujących ze sobą jest sumą ich energii.

Energia całkowita w mechanice jest suma energii potencjalnej i kinetycznej.

Gdy maleje jedna druga rośnie i na odwrót.

Ec=Ek+Ep

Gdzie:

E_k=mv²/2

Ep=mgh,

h- wysokość na które zostało wzniesione ciało.

PRAWA ZACHOWANIA W MECHANICE (SIŁY ZACHOWAWCZE)

Całkowita energia mechaniczna układu ciał, na które działają tylko siły zachowawcze, jest stała. Teza ta wyraża prawo zachowania energii mechanicznej. Podobnie, gdy nie działają siły zewnętrzne: całkowita energia mechaniczna układu zamkniętego, wewnątrz którego działają tylko siły zachowawcze, jest wielkością stałą.

Przy braku sił zewnętrznych zachodzi:
, czyli pęd układu zamkniętego jest stały. Jest to treść prawa zachowania pędu, które można sformułować następująco: pęd zamkniętego układu punktów materialnych jest stały.

Prawo zachowania momentu pędu: moment pędu zamkniętego układu cząstek jest stały.

RUCH BRYŁY SZTYWNEJ

Ruch postępowy - gdy wszystkie punkty bryły sztywnej doznają równych i równoległych przesunięć.

Warunek ruchu postępowego: siła musi być przyłożona do środka masy zgodnie ze środkiem ciężkości.

W tym ruchu miarą bezwładności bryły jest całkowita masa bryły.

Ruch obrotowy - bryła sztywna porusza się w taki sposób, że każdy z punktów bryły, z wyjątkiem punktów leżących na osi obrotu odbywa ruch po kole o promieniu równym odległości od osi obrotu.

Jeśli ruch obrotowy bryły jest jednostajny, to każdy punkt bryły odbywa ruch jednostajny kołowy z prędkością liniową v = r. w ruchu tym każdy z punktów bryły ma przyspieszenie dośrodkowe i podlega działanie siły dośrodkowej. Siła ta nie wywołuje zmian wartości liczbowej prędkości.

W ruchu obrotowym niejednostajnym każdy z punktów bryły ma przyspieszenie normalne i przyspieszenie styczne. Odpowiednio do tych dwóch składowych przyspieszenia możemy mówić o sile stycznej do toru i normalnej do toru, skierowanej wzdłuż promienie. Siła normalna wywołuje zakrzywienie toru. Siła styczna jest odpowiedzialna za zmiany wartości liczbowej prędkości w ruchu obrotowym.

- Ruch postępowy prostoliniowy jest jednostajny, gdy na ciało nie działa żadna siła lub wypadkowa sił działających równa się zeru. Ruch obrotowy jest jednostajny, gdy wypadkowy moment względem osi obrotu wszystkich sił działających na ciało równa się zeru.

- Ruch postępowy prostoliniowy jest zmienny, gdy ciało podlega działaniu siły. Przy ruchu obrotowym działanie siły jest warunkiem koniecznym, ale niewystarczającym do wywołania ruchu obrotowego zmiennego. Tylko taka siła, działająca na ciało obracające się, wywoła zmianę prędkości kątowej, czyli wystąpienie przyspieszenia kątowego , której moment względem osi obrotu nie równa się zeru. (
). Jeżeli moment siły jest skierowany zgodnie z wektorem
to ruch jest przyspieszony. Przy przeciwnym zwrocie momentu działającej siły powstaje ruch obrotowy opóźniony.

ZASADA ZACHOWANIA MOMENTU PĘDU

Suma pędów cząstek, które tworzą układ mechaniczny, nosi nazwę pędu układu.

Widzimy, że w przypadku braku sił zewnętrznych zachodzi
, czyli pęd układu zamkniętego jest stały. Jest to treść prawa zachowania pędu, które można sformułować następująco: pęd zamkniętego układu punktów materialnych jest stały.

Zauważamy, że pęd jest stały i w przypadku układu niezamkniętego, o ile wypadkowa sił zewnętrznych jest równa zeru, a rzut tej sumy na pewien kierunek jest równy zeru, to stały jest pęd w tym kierunku.

Pęd układu można przedstawić w postaci iloczynu całkowitej masy cząstek i prędkości środka masy układu:

.

MOMENT BEZWŁADNOŚCI

Bryła sztywna - jest to takie ciało, w którym pod wpływem działających sił zewnętrznych nie zmienia się wzajemna odległość pomiędzy cząsteczkami tego ciała (siły te nie zmieniają kształtu ciała). Z definicji wynika, że dane ciało czasami możemy traktować jak bryłę sztywną (wtedy, gdy działające siły są zbyt małe aby to ciało odkształcić), a innym razem, gdy działające siły są większe, ciało przestaje być bryłą sztywną. Przyspieszenie kątowe w ruchu bryły sztywnej zależy nie tylko od masy całkowitej, ale także od jej rozłożenia względem osi obrotu. Wielkością charakteryzującą tę własność bryły jest moment bezwładności. Moment bezwładności charakteryzuje więc rozłożenie masy względem osi obrotu. Rozważmy bryłę sztywną będącą zbiorem punktów materialnych m₁,m₂,...,m_n, których odległości od osi obrotu wynoszą odpowiednio r₁,r₂,...,r_n.

Momentem bezwładności I bryły względem danej osi nazywamy sumę iloczynów mas poszczególnych punktów bryły i kwadratów ich odległości od danej osi.

W ruchu obrotowym moment bezwładności odgrywa taką rolę jak masa ciała w ruchu postępowym, ale należy pamiętać o tym, iż moment bezwładności dla jednej i tej samej bryły może być bardzo różny w zależności od położenia osi obrotu. Należy także pamiętać, że moment bezwładności istnieje niezależnie od tego czy ciało się obraca, czy nie. Każde ciało ma moment bezwładności względem dowolnej osi, podobnie jak każde ciało ma masę, niezależnie od tego czy ciało to spoczywa, czy porusza się.

Jest rzeczą oczywistą, że moment bezwładności ciała zależy od wyboru osi obrotu. Dla wielu ciał istnieją osie, względem których moment bezwładności przybiera wartości ekstremalne. Osie te nazywamy głównymi osiami bezwładności, a odpowiadające im momenty - głównymi momentami bezwładności.

PRAWO GRAWITACJI

Siła działająca między każdymi dwoma punktami materialnymi o masach m1 i m2, znajdującymi się w odległości r, jest siłą przyciągającą, skierowaną wzdłuż prostej łączącej te dwa punkty, i ma wartość

Gdzie G jest stałą uniwersalną, mającą tę samą wartość dla wszystkich par punktów materialnych?

Jego cechy:

1. Siły grawitacyjne działające między dwoma dowolnymi ciałami (punktami materialnymi) stanowią parę sił: akcja-reakcja. Pierwsze ciało działa na drugie wzdłuż łączącej je prostej siłą skierowaną do pierwszego ciała. Podobnie, drugie ciało działa na pierwsze siłą skierowaną do drugiego ciała wzdłuż łączącej je prostej. Siły te są równe, co do wartości, ale przeciwnie skierowane.

2. Siła działająca na ciało może być związana z mierzalnymi właściwościami ciała i jego otoczenia, czyli zakładamy istnienie prostych praw rządzących oddziaływaniami ciał.

3. Siła grawitacyjna między dwoma ciałami nie zależy od obecności innych ciał i właściwości otaczającej te ciała przestrzeni.

Prawo powszechnego ciążenia w postaci wektorowej:

Wektor przemieszczenia
, jest skierowany od punktu o masie
do punktu o masie
.

Znak minus w równaniu oznacza, że
ma zwrot przeciwny do
;
podlega działaniu siły skierowanej do
;siła grawitacyjna jest siłą przyciągającą.

DRGANIA HARMONICZNE

Na każdym kroku spotykamy się z drganiami, np.: drgająca struna gitary. Drgania występujące w realnym świecie są zwykle tłumione, ruch stopniowo zanika, a na skutek sił tarcia energia mechaniczne zamienia się w energie termiczną.

Drgania wykresy:

Jedną z ważniejszych własności opisujących ruch drgający jest częstość (częstotliwość), czyli liczba pełnych drgań (cykli) wykonanych w ciągu każdej sekundy. Częstość oznaczamy symbolem ν, a jej jednostką w układzie SI jest herc (Hz)

1 herc= 1 Hz= 1 pełne drganie na sekundę

Z częstością związany jest okres ruchu T, czyli czas w jakim wykonywane jest jedno pełne drganie. T=1/ν

Każdy ruch powtarzający się w regularnych odstępach czasu nazywamy ruchem okresowym. W takim ruchu zależność przemieszczenia x ciała względem początku układu współrzędnych od czasu opisana jest wzorem: x(t)=x_mcos(ωt+φ)

gdzie: x(t)- przemieszczenie w chwili t

x_m- amplituda ω-częstość kołowa φ- faza początkowa (ωt+φ) - faza

x_m, ω,φ- stałe, taki ruch nazywamy ruchem harmonicznym, czyli ruch okresowy opisywany sinusoidalną funkcją czasu.

Wartość x_m nazywamy amplitudą drgań. Jest to dodatnia stała, której wartość zależy od tego jak silne wywołano drgania. Amplituda jest wartością bezwzględną maksymalnego przemieszczenia ciała w obu kierunkach. Zależna os czasu wielkość (ωt+φ) nosi nazwę fazy ruchu.

Ruch harmoniczny (drgania harmoniczne) jest to ruch jaki wykonuje ciało o masie m, na które działa siła proporcjonalna do przemieszczenia, ale o przeciwnym znaku.

DRGANIA TŁUMIONE

Jeżeli nie doprowadzamy do układu drgającego energii, drgania stopniowo zanikają, ich amplituda maleje i wreszcie układ przechodzi w stan spoczynku. Spróbujmy zdać sobie sprawę, jaki będzie przebieg drgań zanikających. W tym celu ułóżmy odpowiednie równanie opierające się na równaniu wyrażającym II zasadę Newtona:

Jest to równanie drgań tłumionych albo zanikających.

Częstość drgań, tzw. drgań własnych, jak wskazuje wzór

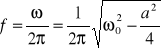
jest zależna od współczynnika a określającego wielkość tłumienia. Gdy ten współczynnik jest bardzo mały, wówczas
możemy zaniedbać wobec
, wtedy
.

Szybkość zanikania drgań zależy od wielkości tego współczynnika. Gdy opór tłumiący jest tak duży, że
, wówczas mamy przypadek tak zwanego ruchu aperiodycznego.

REZONANS MECHANICZNY

Zależność amplitudy drgań wymuszonych od częstości siły wymuszającej prowadzi do tego, że przy pewnej, określonej dla danego układu, częstości amplituda drgań osiąga maksimum. Układ drgający jest szczególnie czuły na działanie siły wymuszającej o tej właśnie częstości. Zjawisko to nazywamy rezonansem, a odpowiednią częstość - częstością rezonansową. A więc częstotliwością rezonansową jest:
. W przypadku braku oporów ruchu amplituda rezonansowa dąży do nieskończoności. W przypadku bardzo silnego tłumienia wyrażenie na częstość rezonansową przyjmuje wartości urojone. Oznacza to, że rezonans nie jest obserwowany - wzrost częstości powoduje, że amplituda drgań wymuszonych monotonicznie maleje.

TRANSFORMACJA LORENTZA

W mechanice relatywistycznej nie tylko miejsce, ale i czas, w którym zaszło pewne zdarzenie W, zależą od przyjętego układu współrzędnych. Jeżeli znamy miejsce (x,y,z) i czas t zdarzenia, w pewnym układzie K, to korzystając z transformacji Lorentza możemy znaleźć miejsce (x',y',z') i czas t', tego samego zdarzenia w układzie K' który porusza się względem układu K z pewną stałą prędkością
.

- prędkość poruszania się układu K' względem K

K - spoczywający układ

K' - poruszający układ

W chwili t₀ układy pokrywały się

X=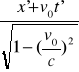
Y= Y' Z = Z' t =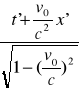

Współrzędne przestrzenne zdarzenia x,y,z ,t dla obserwatora związanego z układem K

X'=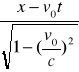
Y'= Y Z' = Z t =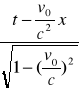

Współrzędne przestrzenne zdarzenia x',y',z' ,t' dla obserwatora związanego z układem K'

Jeżeli wzajemna prędkość v₀ poruszania się obu układów jest dużo mniejsza od prędkości światła, to we wzorach można pominąć (v₀/c)² i otrzymujemy:

X = X' + v₀t' Y = Y' Z = Z' t = t'

X' = X - v₀t Y' = Y Z' = Z t' = t

l=l₀

l - długość pręta mierzona w K

l₀- długość pręta mierzona w K'

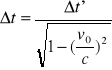
t= t₂ - t₁

t-czas między dwoma zdarzeniami mierzony w układzie K

t'-czas między dwoma zdarzeniami które zaszły w tym samym miejscu układu K'

t'= t'₂ - t'₁ = 

  czas własny

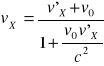
v_y=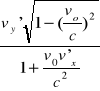
v_z=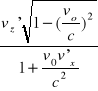

Składowe prędkości
=[v_x,v_y,v_z] w układzie spoczywającym K

Składowe prędkości
'= [v'_x,v'_y,v'_z] w układzie spoczywającym Wasala

DYNAMIKA RELATYWISTYCZNA

Równania Newtona są niezmiennicze względem przekształceń Galileusza, ale nie są niezmiennicze względem przekształceń Lorentza. Nie jest niezmiennicze prawo zachowania pędu. Trzeba zatem tak zdefiniować pęd, by był on niezmienniczy względem transformacji Lorentza. Relatywistyczny wzór na pęd jest więc następujący:
. Druga zasada dynamiki Newtona (w przypadku relatywistycznym) jest określona wzorem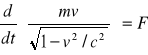
jest niezmiennikiem przekształceń Lorentza. Dostajemy wzór na energię kinetyczną: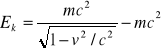
.

Całkowita energia wyraża się wzorem: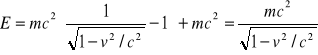
gdzie E₀=mc² jest energią spoczynkową (energią jaką ma cząstka przy V=0). Po wyrzuceniu v z tego wzoru dostajemy:

PRAWO COULOMBA

Ładunkiem punktowym nazywa się naładowane ciało, którego rozmiary można zaniedbać w porównaniu z odległościami tego ciała do innych ciał naładowanych elektrycznie. W wyniku przeprowadzonych przez siebie doświadczeń Coulomb doszedł do wniosku, że siła oddziaływania dwóch nieruchomych ładunków punktowych jest proporcjonalna do każdego z ładunków i odwrotnie proporcjonalna do kwadratu odległości między nimi. Kierunek siły pokrywa się z kierunkiem prostej łączącej te ładunki. Prawo Coulomba można wyrazić wzorem:
. We wzorze tym k, to z założenia dodatni współczynnik proporcjonalności. Doświadczenie pokazuje, że siła oddziaływania dwóch ładunków nie zmienia się, jeżeli w ich pobliżu umieszczone są inne ładunki. Siła oddziaływania między ładunkami znajdującymi się na ciałach o skończonych rozmiarach to wektorowa suma sił między ładunkami punktowymi dq wziętymi parami. Stała k wynosi
, gdzie
.

POLE ELEKTROSTATYCZNE

Polem elektrostatycznym nazywamy własność przestrzeni polegająca na tym, że na umieszczone w tej przestrzeni ciała naelektryzowane (ładunek q)działa siła elektryczna.

Natężeniem pola elektrostatycznego w danym punkcie nazywamy stosunek siły działającej na umieszczony w tym punkcie próbny ładunek dodatni q+ do tego ładunku:

Praca w polu elektrostatycznym zależy od położenia początkowego i końcowego ładunku próbnego Praca w polu elektrostatycznym polega na przesunięciu ładunku między dwoma punktami o różnym potencjale Wz(A-B)=q*U..

Potencjał pola elektrostatycznego jest stosunkiem energii potencjalnej ładunku w tym punkcie pola do tego ładunku.

Na powierzchni ekwipotencjalnej przemieszczenie nie wymaga pracy.

Gęstość objętościowa ładunku:

Gęstość powierzchniowa ładunku na przewodniku kulistym jest jednakowa i równa stosunkowi dostarczonego ładunku do pola powierzchni

Rozkład ładunku na konduktorze jest nierównomierny i zależy od promienia krzywizny.

TWIERDZENIE GAUSSA DLA POLA ELEKTROSTATYCZNEGO

Wielkość Фa= ∫adS nazywa się strumieniem wektora a przez powierzchnię S. Stosunek strumienia Фa do objętości V, z której strumień wypływa Фv/V daje średnią moc właściwą źródeł zawartych w objętości V. Jeśli, w granicy, objętość V zmierza do zera, tj. objętość kurczy się do punktu P, to wyrażenie powyższe określa moc właściwą źródeł w punkcie P. tę moc właściwą nazywamy dywergencją (rozbieżnością) wektora V i oznaczamy symbolem div v. divv=lim
.
Twierdzenie Ostrogradskiego-Gaussa pozwala obliczać dywergencję za pomocą strumienia: ∫adS = ∫divadV, gdzie a - dany wektor.

Cyrkulacją wektora a wzdłuż Ґ nazywamy wyrażenie ∫adl. Rotacją wektora a natomiast nazywamy wyrażenie: (rota)_n =lim
∫adl.

Z twierdzenia Stokesa:

∫adl=∫rota*ds.

Ф_E=∫EdS=∫(∑E_i)ds.=∑∫E_idS=∫EdS=
∑q_i.Uzyskane równanie nosi nazwę twierdzenia Gaussa, które mówi, że strumień wektora natężenia pola elektrycznego przez dowolną powierzchnię zamkniętą równa się sumie algebraicznej ładunków obejmowanych przez tę powierzchnię, podzielonej przez E₀.Wprowadzamy pojęcie gęstości powierzchniowej ładunku q: ç=
.Wtedy możemy twierdzenie Gaussa napisać w postaci różniczkowej: E=div=

DIPOL ELEKTRYCZNY

Dipolem elektrycznym nazywamy układ dwóch równych co do wartości z przeciwnymi znakami ładunków punktowych +q i -q. Znajdują się one w odległości l, która jest dużo mniejsza niż odległość do punktów, gdzie wyznaczane jest pole tego układu.

Prosta przechodząca przez oba ładunki to oś dipola.

Położenie punktu względem dipola charakteryzuje: wektor wodzący r lub współrzędne biegunowe r i 

Wektor l skierowany od ładunku ujemnego do dodatniego jest równy podwójnemu wektorowi a, który wyznacza położenie ładunku względem środka dipola, l=2a.

Odległość danego punktu od ładunków oznaczamy odpowiednio przez r+ i r-, gdzie r=cos/2,

r_--lcos r_-*r₊=r².

POLARYZACJA DIELEKTRYKÓW

Polaryzacja liniowa nie jest jedynym możliwym rodzajem polaryzacji: wektory pola elektromagnetycznego mogą się obracać wokół kierunku rozchodzenia się fali. Mówi się wtedy o polaryzacji kołowej lub ogólniej eliptycznej (kiedy podczas obrotu wektory zmieniają także swoją długość, co powoduje że ich końce zakreślają na płaszczyźnie elipsę). Każdy stan polaryzacji światła można uzyskać jako złożenie dwóch fal spolaryzowanych liniowo w kierunkach wzajemnie prostopadłych o odpowiednio dobranej różnicy faz.

Do wytwarzania i badania światła spolaryzowanego wykorzystuje się polaryzatory. Są to elementy przepuszczające tylko światło o określonym kierunku polaryzacji.

Dielektryki są ośrodkami, w których nie ma swobodnie poruszających się ładunków. Zewnętrzne pole elektryczne rozsuwa ładunki dodatnie i ujemne tworząc w ten sposób dipole elektryczne. Pole elektryczne fali elektromagnetycznej indukuje zatem dipole drgające z częstością taką samą jak częstość drgań pola fali. Z drugiej strony każdy drgający dipol elektryczny jest źródłem promieniowania elektromagnetycznego - wytwarza on falę wtórną nakładającą się na falę padającą. Mechanizm ten powoduje, że wypadkowa fala elektromagnetyczna porusza się z prędkością mniejszą niż w próżni, a kierunek jej rozchodzenia jest inny niż kierunek fali pierwotnej. Jest to szczególnie widoczne, gdy światło przechodzi z jednego ośrodka do drugiego: różne własności tych ośrodków powodują, że kierunek rozchodzenia się wypadkowej fali w drugim ośrodku jest inny niż w pierwszym (fala ulega załamaniu przy przejściu do drugiego ośrodka) i pojawia się dodatkowo fala odbita.

Jeżeli ośrodek, w którym rozchodzi się światło jest niejednorodny to wówczas niektóre z indukowanych drgających dipoli wysyłają promieniowanie wtórne w przypadkowych kierunkach i światło ulega wtedy rozpraszaniu. Przypadkowość kierunku fali rozproszonej ma jednak ograniczenie: drgający dipol elektryczny nie emituje fali elektromagnetycznej w kierunku wzdłuż którego sam drga. Wynika to z faktu, że fala elektromagnetyczna jest falą poprzeczną i stąd nie może się rozchodzić w kierunku drgań natężenia pola elektrycznego (kierunku drgań dipola elektrycznego). Dlatego jeśli w ośrodku niejednorodnym rozchodzi się fala spolaryzowana liniowo, to nie jest ona rozpraszana w kierunku będącym kierunkiem pola elektrycznego tej fali. Dzięki tej własności można jakościowo określić kierunek polaryzacji liniowo spolaryzowanego, obserwując natężenie światła rozpraszanego przez ośrodek rozpraszający. Powyższa własność światła rozpraszanego powoduje również, że rozproszone promieniowanie słoneczne w atmosferze docierające do ziemi jest częściowo spolaryzowane: w świetle rozproszonym nie ma fali o polaryzacji, dla której wektor natężenia pola elektrycznego miałby kierunek zgodny z kierunkiem padania światła słonecznego.

WEKTOR PRZESUNIĘCIA ELEKTRYCZNEGO

dielektryk - substancja nieprzewodząca.

Ładunki wchodzące w skład cząsteczek dielektryka nazywają się ładunkami związanymi. Pod wpływem pola elektrycznego ładunki związane mogą tylko w małym stopniu przesuwać się ze swoich położeń równowagi.

Ładunki, które, mimo iż znajdują się w dielektryku, nie wchodzą w skład poszczególnych cząsteczek, jak również ładunki znajdujące się poza dielektrykiem, nazywają się ładunkami obcymi.

Ładunki związane różnią się od ładunków obcych tylko tym, że nie mogą opuścić granic cząsteczek, w których skład wchodzą. Poza tym ich własności są takie same, jak wszystkich innych ładunków. W szczególności stanowią one źródło pola elektrycznego (dywergencja dodatnia).

Przesunięcie elektrycznym (indukcją elektryczną) i oznaczamy
(wektor przesunięcia elektrycznego):

.

Wielkość
nazywa się względną przenikalnością elektryczną ośrodka (stała materiałowa, bezwymiarowa), zatem

.

w próżni:

w przypadku ładunku punktowego:
.

Jednostką jest kulomb przez metr kwadratowy
.

Jednostką strumienia
jest 1 kulomb.

PRZEWODNIK W POLU ELEKTRYCZNYM

Nośniki ładunku w przewodniku mogą przemieszczać się pod działaniem nawet najmniejszej siły. Z tego względu zaistnienie równowagi ładunków na przewodniku wymaga spełnienia następujących warunków:

1.Natężenie pola w każdym punkcie wewnątrz przewodnika powinno być równe zeru: E = 0

2. Natężenie pola w każdym punkcie powierzchni przewodnika powinno być skierowane wzdłuż normalnej do tej powierzchni: E = E_n.

W ten sposób, w warunkach równowagi ładunkowej, powierzchnia przewodnika jest powierzchnią ekwipotencjalną.

Wprowadzenia nie naładowanego przewodnika do pola elektrycznego powoduje w nim ruch nośników ładunku: dodatnich w kierunku wektora E, ujemnych w przeciwną stronę. W wyniku tego powstają na końcach przewodnika ładunki przeciwnego znaku, nazywane ładunkami indukowanymi. Pole pochodzące od tych ładunków jest skierowane przeciwnie do pola zewnętrznego. Takie gromadzenie się ładunków na końcach przewodnika prowadzi więc do osłabienia występującego w nim pola. Przemieszczanie się nośników ładunku trwa do czasu wypełnienia powyższych warunków, tj. do chwili, gdy natężenie pola wewnątrz przewodnika spadnie do zera, a linie pola na zewnątrz przewodnika staną się prostopadłe do jego powierzchni. W ten sposób obojętny elektrycznie przewodnik, wprowadzony do pola, rozrywa część linii pola, kończą się one na indukowanych ładunkach ujemnych pojawiają się ponownie na indukowanych ładunkach dodatnich. Ładunki indukowane rozkładają się na zewnętrznej powierzchni przewodnika.

SIŁA ELEKTROMOTORYCZNA

Aby otrzymać prąd potrzeba źródła energii elektrycznej np. baterie, generatory itp. Nazywamy je źródłem siły elektromotorycznej SEM. W takich źródłach jeden rodzaj energii jest zamieniany na inny. Siłę elektromotoryczną definiujemy jako stosunek pracy W jako wykonuje ogniwo przy przenoszeniu między biegunami źródła prądu ,ładunku q ;do tego ładunku: E
.

Wielkość ta jest stała i zależy od rodzaju ogniwa. Siła SEM obok oporu wewnętrznego jest wielkością charakteryzującą dane ogniwo.

PRAWO OHMA

Jeżeli do przewodnika przyłożymy różnice potencjałów V, to przez przewodnik popłynie prąd I. Natężenie prądu jest proporcjonalne do przyłożonego napięcia ,dopóki utrzymuje on stałą temperaturę. Przewodnik stawia opór tzw. opór właściwy (rezystancję) :

R=V/I, gdzie R- opór, V -potencjał , I- natężenie.

PRAWO OHMA:

Zakładamy że przewodnik jest jednorodny, prostoliniowy;

Natężenie prądu płynącego wzdłuż jednorodnego, metalicznego przewodnika jest proporcjonalne do spadku napięcia na nadym przewodniku:

,gdzie R- opór, U- napięcie, I- natężenie.

Jednostką Oporu jest [OM]:

.

Opór przewodnika zależy od rozmiarów, kształtu przewodnika i materiału z którego jest wykonany:

, gdzie ρ-opór właściwy (współczynnik materiałowy), l-długość przewodnika, S- pole przekroju poprzecznego przewodnika.

Warto zauważyć że nośnikami prądu w przewodniku są poruszające się (drgające) elektrony, które przenoszą energie. Dlatego możemy nasze rozważania sprowadzić do jednego małego wycinka.

- Jest to tzw. Różniczkowe prawo Ohma.

Poza tym warto wiedzieć że opór stawiany prze przewodnik oprócz powodowania strat energii, jej część zamienia na ciepło wytworzone przez ruch elektronów i związane z tym zderzenia, drgania i tarcie.

POLE MAGNETYCZNE ŁADUNKU W RUCHU

Oddziaływanie prądów odbywa się za pomocą pola nazywanego polem magnetycznym. Pole magnetyczne ma charakter kierunkowy i charakteryzuje się je za pomocą wielkości wektorowej B, nazywanej indukcją magnetyczną. Pole magnetyczne, w odróżnieniu od pola elektrycznego, nie wykazuje działania na ładunek znajdujący się w spoczynku. Pole to powstaje na skutek ruchu ładunków. Spełniona jest zasada superpozycji: pole B wytwarzane przez kilka poruszających się ładunków (prądów) równe jest wektorowej sumie pól B_i wytwarzanych przez każdy ładunek (prąd) z osobna:
.

Gdy v<<c, indukcja magnetyczna pola poruszającego się ładunku wyraża się wzorem:
, gdzie k' jest współczynnikiem proporcjonalności. Jednostką indukcji jest tesla (T).

PRAWO BIOTA - SAVARTA

Prawo, które określa wielkość i kierunek wektora indukcji magnetycznej B w dowolnym punkcie pola magnetycznego, wytworzonego przez prąd elektryczny I. Wartość liczbowa indukcji, wytworzonej przez nieskończenie mały element przewodnika _Dl, jest wprost proporcjonalna do długości elementu przewodnika, natężenia prądu w nim płynącego I oraz sinusa kąta a utworzonego przez kierunki elementu przewodnika i wektora łączącego element z punktem pomiarowym, a odwrotnie proporcjonalna do kwadratu odległości r od punktu pomiarowego do środka elementu przewodnika z prądem

SIŁA LORENTZA

W obecności magnesów lub przewodników z prądem na poruszający się ładunek działa siła prostopadła do kierunku prędkości ładunku, proporcjonalna do wartości ładunku i proporcjonalna do wartości jego prędkości. Silę tę nazywa się siłą Lorentza, a pole powodujące powstanie tej siły nazywa się polem magnetycznym. Siła Lorentza wyraża się wzorem

i wzór ten jest również wzorem, definiującym wektor indukcji magnetycznej
.

PRAWO AMPERA

Wartość całki okrężnej wektora natężenia pola magnetycznego, wytworzonego przez stały prąd elektryczny w przewodniku wzdłuż linii zamkniętej otaczającej prąd, jest równa sumie algebraicznej natężeń prądów obejmowanych przez tę linię.

Natężenie pola magnetycznego - H - wielkość wektorowa charakteryzująca pole magnetyczne, wytworzone przez poruszające się ładunki i prądy, i niezależna od magnetycznych właściwości ośrodka. Natężenie pola jest liczone w punkcie i zależne jest od rozkładu przewodników z prądem. Im silniejszy prąd płynie w przewodniku, tym większa wartość natężenia pola w każdym punkcie otaczającej przestrzeni.

OBWÓD Z PRĄDEM W POLU MAGNETYCZNYM

Prąd jest zbiorem poruszających się ładunków. Ponieważ pole magnetyczne wywiera działanie odchylające na poruszający się ładunek, spodziewamy się, że będzie ono także odchylał przewodnik, w którym płynie prąd.

Prąd i w metalowym przewodniku jest przenoszony przez swobodne elektrony(elektrony przewodnictwa).

gdzie l jest wektorem o wartości równej długości drutu, o kierunku wyznaczonym przez (prosty) drut i zwrocie określonym przez kierunek prądu.

Równanie to jest równoważne związkowi

wektor l jest skierowany w lewo i siła magnetyczna F jest skierowana przed płaszczyznę kartki.

Aby znaleźć siłę działającą na dowolny przewodnik nie prostoliniowy całkujemy następujący wzór:

WŁASNOŚCI WEKTOROWE POLA MAGNETYCZNEGO

W otoczeniu magnesu stwierdzamy dwojakiego rodzaju działania

1) dynamiczne (wywieranie sił na inne magnesy)

2) indukcyjne (magnesowanie kawałków stali).

Przestrzeń, w której występują te działania, nazywamy polem magnetycznym.

Wyobraźmy sobie, że mamy malutki, punktowy biegun magnetyczny dodatni należący do bardzo długiego liniowego magnesu. Na biegun próbny dodatni o natężeniu b działa siła w każdym punkcie pola magnesu siła
. Siła ta jest proporcjonalna do b. Zatem stosunek
będzie jedynie zależał od miejsca w polu. Nazywamy go natężeniem pola magnetycznego w danym punkcie. Będzie to wektor o kierunku siły wywieranej na biegun północny. Oznaczamy do zwykle literą
:

Pole magnetyczne, w którym wektor magnetyczny jest stały co do kierunku i wielkości, nazywamy jednostajnym albo jednorodnym.

Pole magnetyczne, którego natężenie jest niezmienne w czasie i posiadające tę własność, że praca wykonana przez siły pola przy ruchu bieguna magnetycznego po dowolnym obwodzie zamkniętym równa się zeru, nazywa się polem magnetycznym statycznym albo polem magnetostatycznym. Pola pochodzące od magnesów trwałych nieruchomych są polami magnetycznymi statycznymi.

INDUKCJA ELEKTROMAGNETYCZNA

W zamkniętym, przewodzącym obwodzie, na skutek zmiany strumienia indukcji magnetycznej przez powierzchnię ograniczoną tym obwodem, powstaje prąd elektryczny. Zjawisko to nosi nazwę indukcji elektromagnetycznej, a powstający prąd - prądu indukcyjnego. Zjawisko indukcji elektromagnetycznej świadczy o tym, że podczas zmian strumienia magnetycznego powstaje w obwodzie siła elektromagnetyczna E_i. Wartość E_i nie zależy od sposobu, w jaki dokonuje się zmian strumienia Φ, zależy natomiast od szybkości tych zmian:
. Zmianie znaku
towarzyszy zmiana kierunku działania E_i.

Reguła Lenza głosi, że prąd indukcyjny jest zawsze skierowany tak, aby przeciwdziałać przyczynie, która go wywołuje. A więc
i E_i mają przeciwne znaki.

SAMOINDUKCJA

Polega na powstawaniu w obwodzie SEM indukcji na skutek zmiany natężenia prądu w tym obwodzie. Jak wiadomo jeżeli w obwodzie płynie prąd, to wywołuje on w swoim otoczeniu pole magnetyczne, którego linie przenikają powierzchnię ograniczoną zwojem. Ponieważ indukcja pola magnetycznego
wytworzonego w otoczeniu obwodu z prądem jest, zgodnie z prawem Biota-Savarta, w każdym punkcie proporcjonalna do wartości prądu płynącego przez obwód, to również strumień indukcji Φ_B przenikający obwód jest do niego proporcjonalny - czyli można zapisać Φ_B = LI. Stosując prawo indukcji Faradaya otrzymujemy wzór na SEM samoindukcji :

RÓWNANIE MAXWELLA

1)Prawo Gaussa dla pola elektrycznego:

Strumień wektora indukcji elektromagnetycznej D przez zamkniętą powierzchnię jest równy ładunkowi znajdującemu się w obszarze ograniczonym tą powierzchnią. Prawo to wyraża fakt że pole elektrostatyczne jest polem źródłowym.

2)Prawo Gaussa dla pola magnetycznego:

Strumień wektora indukcji magnetycznej przez zamkniętą powierzchnię jest zawsze równy zeru. Mówimy że pole magnetyczne jest polem bezźródłowym.

3)Prawo indukcji elektromagnetycznej:

Prawo indukcji Faradaya głosi, że indukowana w obwodzie elektrycznym SEM równa jest szybkości, z jaką zmienia się strumień przechodzący przez ten obwód. Znak minus dotyczy kierunku indukowanej SEM, przeciwstawiającej się kierunkowi płynącego w obwodzie prądu elektrycznego.

4)Prawo Ampera:

Krążenie wektora H wzdłuż krzywej zamkniętej równa się całkowitemu prądowi przechodzącemu przez powierzchnię ograniczoną tą krzywą. Zmiana w czasie wektora D powoduje powstanie wirowego pola magnetycznego.

DRGANIA ELEKTRYCZNE

Analizując drgania elektryczne, mamy do czynienia z prądami zmieniającymi się w czasie. W obwodzie zawierającym indukcyjność i pojemność mogą powstawać drgania elektryczne. Stąd obwód taki nazywa się obwodem drgającym. Drgania w obwodzie można wywołać przez naładowanie kondensatora lub przez wzbudzenie prądu w elemencie obwodu o niezerowej indukcyjności (np. przez włączenie zewnętrznego pola magnetycznego, przenikającego zwoje cewki). Każdy obwód rzeczywisty ma różny od zera opór czynny. Drgania swobodne tłumione w obwodzie RLC(opornik, solenoid, kondensator) możemy zapisać w postaci:
.

RÓWNANIE FALOWE

Równanie falowe to matematyczne równanie różniczkowe cząstkowe drugiego rzędu, opisujące ruch falowy.

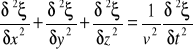
, k- liczba falowa.

Równanie powstaje po dwukrotnym zróżniczkowaniu funkcji:

i dodaniem pochodnych względem współrzędnych.

ZASADA FERMATA

Ten dział optyki, w którym zaniedbuje się skończone wartości długości fal, nazywamy optyką geometryczną.

Podstawę optyki geometrycznej stanowią cztery prawa:

Prawo prostoliniowego rozchodzenia się światła stanowi, że w ośrodku jednorodnym światło rozchodzi się prostoliniowo.

Prawo niezależności promieni świetlnych stanowi, że przecinające się promienie świetlne nie zaburzają się wzajemnie. W przypadku bardzo dużych natężeń światła, osiąganych za pomocą laserów, niezależność promieni świetlnych przestaje obowiązywać.

Z zasady Fermata wynika prawo prostoliniowego rozchodzenia się oraz prawo odbicia i załamania światła. W sformułowaniu samego Fermata zasada ta głosi, że światło rozchodzi się po takiej drodze, która wymaga najkrótszego czasu. Z zasady Fermata wynika odwracalność promieni świetlnych. Faktycznie, droga optyczna wykazująca minimum przy przejściu od punktu l do punktu 2 będzie również drogą minimalną w przypadku rozchodzenia się światła w kierunku odwrotnym. ((Światło biegnie między dwoma dowolnymi punktami po takiej drodze, aby czas potrzebny na jej przebycie był jak najkrótszy lub jak najdłuższy.))

WSPÓŁCZYNNIK ZAŁAMANIA

Jest to wielkość charakteryzująca właściwości optyczne ciał przezroczystych. Rozróżnia się dwa współczynniki załamania światła:

1)bezwzględny -jest to stosunek prędkości światła w próżni do prędkości światła w danym ośrodku n=c/v

2)względny - stosunek prędkości światła w jednym ośrodku do prędkości światła w drugim ośrodku, równy liczbowo stosunkowi sinusa kąta padania a światła na granicę dwóch ośrodków między ośrodkami do sinusa kąta załamania w ośrodku drugim : n= sin/ sin

Dla danej substancji współczynnik załamania zależy od ciśnienia, temperatury, długości fali.

Względny w.z. Decyduje o tym, jak bardzo światła ma tendencję do skręcania swego kierunku podczas przechodzenia do innego ośrodka.

Przy dużym względnym w.z. Światło będzie się silniej załamywać: dla powietrza 1.00 , dla wody 1.33

PRYZMAT PROSTY

Pryzmat prosty tworzą dwie płaszczyzny schodzące się pod kątem φ, ograniczające jednorodny, przezroczysty materiał. Kąt ten nazywamy kątem łamiącym pryzmatu.

Pryzmaty złożone, budowane dla specjalnych celów, mogą służyć do rozszczepiania wiązki światła, do zmiany kierunku wiązki światła bez rozszczepiania i do polaryzacji światła.

Pryzmat prosty, pojedynczy zawsze rozszczepia wiązkę światła białego jak i zmienia jej bieg. Działanie jego oparte jest na zjawisku dyspersji światła, czyli różnej wartości współczynnika załamania światła dla fal o różnej częstotliwości v. Każda ze składowych równoległej wiązki światła białego (będącego mieszaniną fal o różnej częstotliwości v), padająca na jedną ze ścian pryzmatu przyległą do kąta łamiącego, załamuje się na niej pod innym kątem i biegnie z inną prędkością wewnątrz pryzmatu, przechodząc przez pryzmat i wychodząc powtórnie się załamuje, tworząc barwną wiązkę rozbieżną

Soczewka

Najprostszy centryczny układ optyczny stanowi soczewka. Jest nią przezroczyste ciało (zwykle szklane) ograniczone dwiema powierzchniami kulistymi (jedna z powierzchni może być płaska). Punkty przecięcia powierzchni z osią optyczną soczewki nazywamy wierzchołkami powierzchni załamujących. Odległość miedzy wierzchołkami stanowi grubość soczewki.

Podstawową funkcją soczewek jest koncentryczne (względem osi) skupianie lub rozpraszanie światła. Stąd każda soczewka posiada oś optyczną i punkt skupienia (tzw. ognisko soczewki).

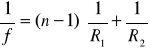
R1 i R2 - promienie krzywizny; f - ogniskowa; n - wspł. załamania soczewki

Dyspersja

Dyspersja - w optyce to zależność współczynnika załamania n ośrodka (np. szkła) od długości fali.

INTERFERENCJA

Jeżeli różnica faz
drgań wywołanych przez fale jest stała w czasie, to fale nazywa się falami spójnymi.

Podczas nakładania się spójnych fal świetlnych zachodzi zmiana rozkładu strumienia świetlnego w przestrzeni, w wyniku czego w pewnych miejscach powstają maksima, a w innych - minima natężeń. Zjawisko to nazywamy interferencja fal.

Spójne fale świetlne można otrzymać rozdzielając falę emitowaną przez jedno źródło na dwie części. Jeżeli spowodujemy potem, żeby te dwie fale przebyły różne drogi optyczne, a następnie nałożymy je wzajemnie, to interferencja wystąpi.

Warunek interferencyjnego maksimum (jeżeli różnica dróg optycznych jest równa całkowitej krotności długości fali w próżni to różnica faz
jest krotnością
i drgania wytwarzane w punkcie P przez obie fale odbywają się w jednakowej fazie):

(m = 0,1,2,…)

Warunek interferencyjnego minimum (jeżeli
jest równa połówkowej krotności długości fali w próżni, to
, co oznacza, że drgania w punkcie P znajdują się w przeciwfazie):

(m = 0,1,2,…).

DYFRAKCJA FRESNELA

Każdy element powierzchni falowej stanowi źródło kulistej fali wtórnej, której amplituda jest proporcjonalna do wielkości tego elementu. Amplituda fali kulistej maleje wraz z odległością od źródła jak 1/r.

POLARYZACJA SWIATŁA

Spolaryzować można tylko falę poprzeczną. Teoria przewiduje, że światło podobnie jak inne fale elektromagnetyczne jest falą poprzeczną. Kierunek drgań wektorów E (natężenie pola elektrostatycznego) i B(wektor indukcji pola magnetycznego) tworzących falę świetlną są prostopadłe do kierunku rozchodzenia się fali. Drgający wektor E tworzy z kierunkiem rozchodzenia się fali płaszczyznę drgań .

Rysunek fali niespolaryzowanej.

Rysunek fali spolaryzowanej

Jest kilka sposobów na spolaryzowanie światła.

-Użycie polaroidu czyli płytki polaryzującej. Na płytce istnieje charakterystyczny kierunek polaryzacji zaznaczony liniami równoległymi .Płytka przepuszcza tylko te fale dla których kierunki drgań wektora E są równoległe do wektora polaryzacji. Obok ustawiamy drugą płytkę analizator .Amplituda fali wychodzącej z analizatora wynosi Ecosφ gdzie φ kąt między kierunkami polaryzacji obu płytek. Wynika z tego prawo Malusa dane wzorem:

J = Jm,cos^2φ	J - natężenie światła wychodzącego z analizatora
		Jm - natężenie światła wychodzącego z polaryzatora

-Polaryzacja przez odbicie. Nastawiając odpowiednio kąt padania wiązki na szkło lub (inne dielektryki) można doprowadzić do polaryzacji promienia odbitego. Doświadczalnie stwierdzono, że po ustaleniu kąta odbicia który spełnia zależność :

tgα = n_2,1 gdzie n- względny współczynnik załamania materiału odbijającego,

Dochodzi do całkowitej polaryzacji promienia odbitego. Zachodzi to wtedy gdy promień padający i odbity są względem siebie pod kątem prostym.

-Rozchodzenie się światła w ośrodkach anizotropowych .Są to materiały w których różne własności światła np. prędkość światła i jego polaryzacja zależą od kierunku rozchodzenia się światła w materiale.

EFEKT DOPPLERA

Zjawisko Dopplera - pozorna zmiana częstotliwości fali odbieranej przez obserwatora, gdy obserwator i źródło poruszają się względem siebie. Gdy się zbliżają częstotliwość rośnie, gdy oddalają- maleje. W optyce to zjawisko polega na zmianie barwy światła.

Światło tak jak dźwięk ma strukturę falową. Możemy, więc zjawisko Dopplera z dźwięku przenieść na światło.

ω - częstość odbierana, ω₀ - częstość emitowana

I ZASADA TERMODYNAMIKI

Przejściu od 1 stanu do 2 odpowiada zmiana energii wewnętrznej U układu. Ta zmiana energii wewnętrznej wiąże się z ciepłem Q (doprowadzonym do układu lub oddanym przez układ) i z pracą W (wydaną lub dostarczoną).

Q = U + W

Oznacza to, że kosztem ciepła Q doprowadzonego do układu uzyskuje się wzrost jego energii wewnętrznej U oraz pracę przez niego wykonaną W. Równanie to w sposób ogólny wyraża treść I zasady termodynamiki. U nie zależy od rodzaju przemiany. Q i W mogą ulegać zmianie w zależności od charakteru przemiany. Q i W nie są funkcjami stanu układu, tzn. nie charakteryzują jego stanu, lecz przemianę, jakiej podlega układ.

Przemiana zamknięta ( w tej przemianie U=0): Q = W lub δQ = δW

Zastosowanie I zasady termodynamiki do izoprzemian gazu doskonałego.

Izoprzemiana - przemiana, przy której jeden z parametrów charakteryzujących stan ciała pozostaje stały.

1.przemiana izotermiczna

W przemianie izotermicznej T =const więc U₁=U₂ czyli U = 0 więc w przemianie izotermicznej gazu doskonałego ciepło zamienia się całkowicie na pracę lub odwrotnie. Q = W.

2.przemiana izobaryczna

Ogrzewamy 1 mol gazu doskonałego o dT pod stałym ciśnieniem. Przyrost energii wewnętrznej podczas ogrzewania o dT wynosi dU. Gaz zwiększa swoją objętość o dVm a więc wykonana praca dW = pdV_m

3.przemiana izochoryczna

W elementarnej przemianie izochorycznej V=0 więc i W=0, z I zasady termodynamiki : dQ = dU. Doprowadzenie ciepła do ciała przy niezmienionej objętości powoduje wzrost jego energii wewnętrznej równy dostarczonej energii cieplej.

4.przemiana adiabatyczna

W tej przemianie nie ma wymiany ciepła z otoczeniem.

dQ = 0 więc dU = - dW

W czasie adiabatycznych zmian objętość ciśnienia zmienia się gwałtowniej niż podczas przemian izotermicznych.

PROCESY GAZU DOSKONAŁEGO

Gaz doskonały - gaz cząsteczek o pomijalnej własnej objętości cząsteczek, które mogą się ze sobą sprężyście zderzać, ale ich energia potencjalna wzajemnego oddziaływania wynosi zero. Cząstki te posiadają tylko energię kinetyczną.

ADIABATYCZNY PROCES, adiabatyczna przemiana, proces termodynamiczny, podczas którego układ jest izolowany adiabatycznie, tj. naczynie w którym znajduje się gaz ma wykonane ścianki z doskonałego izolatora cieplnego. Praca wykonana nad układem w procesie adiabatycznym jest równa przyrostowi energii wewnętrznej. W procesie adiabatycznym odwracalnym entropia układu pozostaje stała, w procesie adiabatycznym nieodwracalnym entropia układu rośnie.

IZOBARYCZNY PROCES, izobaryczna przemiana, proces termodynamiczny, podczas którego ciśnienie nie ulega zmianie; np. reakcje chem. zachodzące pod stałym ciśnieniem; praca wykonana przez gaz rozprężający się izobarycznie od objętości V₁ do objętości V₂ wynosi L = p(V₂ -V₁), gdzie p — ciśnienie gazu; proces izobaryczny dla gazu doskonałego opisuje prawo Gay-Lussaca, podające zależność objętości gazu od temp. przy stałym ciśnieniu.

IZOCHORYCZNY PROCES, izochoryczna przemiana, proces termodynamiczny, podczas którego układ nie zmienia objętości; np. reakcje chem. zachodzące w gazach w zamkniętych naczyniach; proces izochoryczny dla gazu doskonałego opisuje prawo Charlesa.

IZOTERMICZNY PROCES, izotermiczna przemiana, proces termodynamiczny, podczas którego temperatura układu nie ulega zmianie; np. przemiany fazowe (topnienie, parowanie, sublimacja); praca wykonana przez układ w odwracalnym procesie izotermicznym jest równa ubytkowi jego energii swobodnej; proces izotermiczny dla gazu doskonałego opisuje prawo Boyle'a i Mariotte'a, które brzmi ze w stałej temp obj. gazu jest odwrotnie proporcjonalna do ciśnienia , tzn. p*V = const.

CYKL CARNOTA

Cykl Carnota jest to odwracalny kołowy proces, podczas którego następuje zamiana energii wewnętrznej na mechaniczną (potocznie ciepła na prace).

Pojęcie cyklu Carnota łączy się bezpośrednio z pojęciem silnika Carnota, wyidealizowanego urządzenia, w którym ten proces jest stosowany. Silnik ten ma największą możliwą sprawność a substancją roboczą jest tu gaz doskonały.

Cykl Carnota składa się z czterech procesów:

Izotermiczne rozprężanie - podczas tego procesu substancja robocza pobiera ciepło (od grzejnika). Zachowywana jest przy tym stała temperatura gazu. Ciepło jest w całości zamieniane na pracę, gdyż energia wewnętrzna gazu jest stała. Aby praca ta była maksymalna, przemianę doprowadzimy do momentu, w którym wyczerpie się cały dostępny na ten cykl zapas ciepła. Znajdziemy się wtedy w punkcie B.

Adiabatyczne rozprężanie - cała dostępna na ten cykl energia cieplna została już wykorzystana. Jednak nie jest to kres możliwości uzyskiwania pracy, gdyż teraz gaz może ją wykonać kosztem zawartej w nim energii wewnętrznej. Dzięki temu ogólna praca wykonana podczas cyklu ulegnie dodatkowemu zwiększeniu. Na tym etapie nie ma wymiany ciepła z otoczeniem (adiabata!). Temperatura ciała roboczego spada.

Izotermiczne sprężanie - podczas tej przemiany ciepło jest oddawane (do chłodnicy). Temperatura pozostaje bez zmian, praca jest do układu dostarczana.

Adiabatyczne sprężanie - podczas tego procesu temperatura ciała roboczego wzrasta, aż osiągnie wartość równą temperaturze grzejnika. Podobnie jak przy procesie drugim, tu także nie ma wymiany ciepła z otoczeniem. Praca wykonana przez siły zewnętrzne podczas sprężania, powoduje przyrost energii wewnętrznej.

Współczynnik wydajności cyklu Carnota jest równy:

gdzie: T₂ - to temperatura grzejnicy, T₁ - temperatura chłodnicy.

II ZASADA TERMODYNAMIKI

Została sformułowana na kilka sposobów:

-entropia układu izolowanego nie może maleć, czyli każdemu procesowi nieodwracalnemu towarzyszy wzrost entropii

-niemożliwe są procesy, których jedynym następstwem jest przepływ ciepła od ciała o niższej temperaturze do ciała o wyższej temperaturze (Clausius)

-niemożliwe są procesy, których jedynym rezultatem jest pobranie ciepła od pewnego ciała i całkowita zmiana tego ciepła na pracę (Kelvin).

ENTROPIA UKŁADU

Entropia jest funkcją stanu układu, której różniczka w elementarnym procesie odwracalnym jest równa nieskończenie małej ilości ciepła dostarczonej układowi, do temperatury bezwzględnej układu. Na podstawie zmian entropii można wnioskować o kierunku procesu wymiany ciepła. Podczas ogrzewania ciała entropia wzrasta, podczas ochładzania - maleje. Zmiana entropii w dowolnym procesie odwracalnym przeprowadzającym układ ze stanu 1 do stanu 2 jest równa ciepłu zredukowanemu oddawanemu przez układ w tym procesie.

Jeżeli w trakcie procesu entropia nie ulega zmianie, to taki proces jest procesem izoentropowym (np. odwracalny proces adiabatyczny ma δQ=0 i S=const.).

Entropia układu fizycznie jednorodnego jest funkcją dwóch niezależnych parametrów stanu, np.: dla procesu izochorycznego parametry to V i T, dla procesu izobarycznego parametry to p i T, przy czym oba procesy powodują ogrzewanie układu od temperatury.

RÓWNANIE TEORII KINETYCZNO-MOLEKULARNEJ

Teoria ta opiera się na następujących założeniach ogólnych:

1. Ciała mają budowę nieciągłą; składają się z drobnych elementów w postaci atomów lub cząsteczek (molekuł)
  2. Wymienione elementy są w ciągłym ruchu. Wartości liczbowe i kierunki prędkości poszczególnych elementów są różne.
  3. Pomiędzy poszczególnymi elementami budowy ciał występują siły wzajemnego  oddziaływania.

Podstawowym równaniem kinetycznym gazów jest:
gdzie k - stała Boltzmanna, T - temp. gazu

WZÓR BAROMETRYCZNY

- wzór barometryczny - z tego wzoru wynika, że ciśnienie maleje tym szybciej z wysokością, im cięższy jest gaz (im większa masa cząsteczkowa powietrza μ) oraz im niższa jest temperatura atmosfery.

ZASADA EKWIPARTYCJI

Czyli zasada równego rozkładu energii na stopnie swobody cząsteczki. Na każdy stopień swobody cząsteczki związany z ruchem postępowym i obrotowym przypada średnio taka sama energia kinetyczna kT/2. Wzór na średnią energię cząsteczki w przypadku, gdy nie ma oscylacji atomów (wiązania są sztywne) ma postać:

=
k = 1,38×10^-23 J/K-stała Boltzmana

k=R/N_A N_A-liczba Avogadro N_A=6,022×10²³mol^-1

R - stała gazowa R = 8,31
T- temperatura bezwzględna gazu

i - ilość stopni swobody cząstki

i = i_post. + i_obr.

i_post - liczba stopni swobody ruchu postępowego

i_obr. - liczba stopni swobody ruchu obrotowego

GAZ VAN DER WAALSA

Zachowanie się rzeczywistych gazów jest dobrze opisywane równaniem ρV_m=RT , o ile objętość gazu jest niewielka, tzn. ciśnienie jest zbyt duże, a temperatura jest dostatecznie wysoka. Wraz ze wzrostem ciśnienia i ze spadkiem temperatury obserwuje się znaczne odstępstwa od tego równania, gdyż wzrost gęstości gazu powoduje, że duża rolę zaczyna objętość cząsteczek, a tym samym zderzenia międzycząsteczkowe.

Równanie van der Waalsa (opisujące zachowanie się gazów szerokim zakresie gęstości):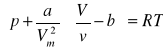
, gdzie p jest ciśnieniem wywieranym na gaz z zewnątrz (równym ciśnieniu wywieranym na ścianki naczynia), natomiast a i b oznaczają stałe van der Waalsa, przyjmujące różne wartości dla różnych rzeczywistych gazów (wyznacza się je doświadczalnie). Gazy rzeczywiste spełniają równanie van der Waalsa jedynie w przybliżeniu. Abstrakcyjny gaz, spełniający to równanie nazywamy gazem van der Waalsa. Energia wewnętrzna tego gazu powinna zawierać, oprócz energii kinetycznej cząsteczek, także energię wzajemnego oddziaływania cząsteczek.

ZAŁOŻENIA FIZYKI STATYSTYCZNEJ

Prawo równowagi termodynamicznej mówi, że każdy stan mikroskopowy jest jednakowo prawdopodobny. Hipoteza ergodyczna stwierdza, iż uśrednianie po czasie jest równoważne uśrednianiu po zespole statystycznym. Zespołem statystycznym nazywamy zbiór identycznych układów, znajdujących się w takim samym stanie. Niech
będzie energią wewnętrzną układu, Q(E) - zespołem stanów mikroskopowych, a Ω(E) - liczbą stanów mikroskopowych. Jeżeli prawdopodobieństwa znalezienia układu izolowanego w dowolnym stanie
są jednakowe, to układ znajduje się w stanie równowagi.

TEMPERATURA I ENTROPIA STATYSTYCZNA

Entropia statystyczna jest to:

- logarytmiczna miara liczby dowolnych stanów

- miara nie uporządkowania cząsteczek w układzie (ilościowa miara stopnia cząsteczkowego chaosu w układzie)

Wyraża się wzorem: S = klnW,

gdzie: k - stała Boltzmana (
)

W - liczba sposobów na które może być zrealizowany dany układ.

Własności entropii:

1. S układu izolowanego w wyniku procesów nieodwracalnych rośnie (w istocie, układ izolowany przechodzi przez stany o różnych prawdopodobieństwach, w wyniku czego S wzrasta)

2. S układu w stanie równowagi jest maksymalna.

Prawo wzrostu entropii:

Entropia układu izolowanego może jedynie rosnąć.

Im wyższa temperatura układu (wyższa E _wew. ) tym względnie mniejsza jest rola nieuporządkowania, uwarunkowanego doprowadzeniem danej ilości ciepła.

Temperatura statystyczna wyraża się wzorem: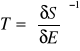

Temperatura jest odwrotnością pochodnej cząstkowej entropii po energii.

ROZKŁAD PRĘDKOŚCI MAXWELLA

Rozkład Maxwella-Boltzmanna podaje jaki ułamek ogólnej liczby cząsteczek gazu doskonałego porusza się w danej temperaturze z określoną szybkością - zależność ta ma charakter gęstości prawdopodobieństwa. Założeniem jest równowaga termiczna gazu.

((Opiszmy ilościowo rozkład prędkości cząsteczek. W tym celu wyobraźmy sobie przestrzeń prędkości, którą nazwiemy v-przestrzenią. Wprowadzamy prostokątny układ współrzędnych: vx, vy, vz. Prędkości każdej cząsteczki odpowiada punkt w v-przestrzeni. Z powodu zderzeń położenia punktów ciągle się zmieniają, lecz ich gęstość w każdym miejscu pozostaje stała. Wszystkie kierunki są jednakowo uprawnione. Gęstość punktów w v-przestrzeni może więc zależeć tylko od modułu prędkości v.

Na podstawie liczby cząsteczek (ogólnej), liczby cząstek znajdujących się w tym obszarze (których prędkość jest zawarta w przedziale <v, v+dv>) oraz objętości tego obszaru wyznaczamy prawdopodobieństwo dPv

tego, że prędkość danej cząsteczki jest z przedziału od v do v+dv. Stąd otrzymujemy funkcję F(v) rozkładu prędkości cząsteczek gazu.))

ZJAWISKO FOTOELEKTRYCZNE

zjawisko fotoelektryczne - zjawisko fizyczne polegające na emisji elektronów z powierzchni przedmiotu (tzw. efekt zewnętrzny) lub na przeniesieniu nośników ładunku elektrycznego pomiędzy pasmami energetycznymi (tzw. efekt wewnętrzny), po naświetleniu jej promieniowaniem elektromagnetycznym (na przykład światłem widzialnym) o odpowiedniej częstotliwości, zależnej od rodzaju przedmiotu. Emitowane w ten sposób elektrony nazywa się czasem fotoelektronami. Energia kinetyczna fotoelektronów nie zależy od natężenia światła a jedynie od jego częstotliwości.

h ν = W + E_k

gdzie: h - stała Plancka;

ν - częstość padającego fotonu;

W - praca wyjścia (potrzebna do usunięcia elektronu z substancji, charakterystyczna dla danej substancji);

E_k - maksymalna obserwowana energia kinetyczna emitowanych elektronów.

EFEKT COMPTONA

Rozpraszanie komptonowskie (zjawisko Comptona) polega na oddziaływaniu kwantów γ z elektronami, które możemy traktować jako swobodne. W wyniku takiego oddziaływania kwant γ zmienia kierunek ruchu oddając część energii elektronowi. Zauważmy, że przy typowych energiach promieniowania gamma elektrony znajdujące się na ostatnich orbitach można traktować jak elektrony swobodne.

Wszystkie z omawianych zjawisk: efekt Comptona, zjawisko fotoelektryczne czy też tworzenie się par elektron-pozyton powodują usunięcie danego kwantu γ z wiązki.

PROMIENIOWANIE ROENTGENA

Promieniowanie rentgenowskie powstają w wyniku bombardowania twardych tarcz szybkimi elektronami. Lampa rentgenowska ma postać próżniowego balonu zawierającego kilka elektrod. Grzana prądem katoda K stanowi źródło swobodnych elektronów wytworzonych na skutek termoemisji. Elektrony przyspieszane są wysokim napięciem przyłożonym pomiędzy katodę i antykatodę. Prawie cała energia elektronów wydzielana jest na antykatodzie w postaci ciepła. Do lamp rentgenowskich przykładane są napięcia do 50kV. Po przejściu takiej różnicy potencjałów elektron osiąga prędkość 0,4c. Im mniejsza jest długość fali tym słabiej promieniowanie pochłaniane jest przez materię.

FALE DE BROGLIE'A

W zjawiskach optycznych widoczny jest osobliwy dualizm. Oprócz takich własności światła, które w bezpośredni sposób świadczą o jego naturze falowej (interferencja, dyfrakcja), obserwujemy również i inne własności, równie bezpośrednio świadczące o jego własnościach korpuskularnych (zjawisko fotoelektryczne, zjawisko Comptona).

W roku 1924 Luis de Broglie wysunął śmiałą hipotezę, że dualizm cechuje nie tylko zjawiska optyczne, ale ma znaczenie uniwersalne. Zakładając, że materialne cząstki oprócz własności korpuskularnych mają także i falowe, de Broglie przeniósł na przypadek materialnych cząstek obowiązujące w przypadku światła reguły przechodzenia od obrazu falowego do korpuskularnego. Foton ma energię
i pęd

Według hipotezy de Broglie'a ruch elektronu lub jakiejkolwiek innej cząstki związany jest z procesem falowym o długości fali
i częstości

Hipoteza de Broglie'a została w krótkim czasie potwierdzona doświadczalnie. Falę „towarzyszącą” cząsteczce nazywa się falą de Broglie'a.

DOŚWIADCZENIE RUTHERFORDA

Cząstka alfa - jądro atomu helu, tj. struktura złożona z silnie ze sobą związanych 2 protonów i 2 neutronów. Liczba atomowa (ładunek) cząstki α wynosi 2, liczba masowa 4. Cząstki α są np. emitowane w wyniku przemiany jądrowej zwanej przemianą α.

W roku 1911 Ernest Rutherford wykonał doświadczenie nad rozpraszaniem cząstek α przez cienką folię złota. Grubość folii użytej w doświadczeniu wynosiła 0,4μm, co odpowiada 2000 warstw atomowych. Na drodze cząstek α, wybiegających przez szczelinę D z naczynia R zawierającego sól uranową (emitującą cząstki α), ustawiona jest cienka metalowa folia F. Niektóre z cząstek α , rozproszonych przez metalowa folię, padają na przeźroczysty ekran S wywołując scyntylacje (rozbłyski). Można je obserwować przez mikroskop M, do którego obiektywu przymocowany jest ekran fluoryzujący. W urządzeniu istnieje możliwość obracania układu naczynie- folia. Z wnętrza aparatury wypompowane jest powietrze, aby cząstki α nie zderzały się z cząsteczkami powietrza.

W doświadczeniu określano liczbę cząstek (scyntylacji) odchylonych o różne kąty od pierwotnego kierunku. Stwierdzono, że większość cząstek przechodziła przez folie bez wyraźnego odchylenia, co świadczy o tym, że folia i atomy są dla cząstek α przeźroczyste. Zaskakującym faktem było rozproszenie cząstek pod dużymi kątami, a przede wszystkim zarejestrowanie cząstek po tej samej stronie folii, z której padła wiązka. Cząstka α nie może ulec odchyleniu na skutek zderzenia z elektronem, ponieważ jej masa jest przeszło 7000 razy większa od masy elektronu. Przyczyną odchylenia musi być zderzenie z atomem. Obserwowane rozproszenie cząstek α pod dużymi kątami było niezgodne z przewidywaniami opartymi na modelu Thomsona, niezależnie od tego czy założyło się, że odchylenie cząstki α następuje w wyniku pojedynczego zderzenia z atomem o promieniu 10^-10 m, czy też w wyniku zderzeń wielokrotnych.

Rutherford doszedł do przekonania, że pole elektryczne wytworzone wewnątrz atomu przez dodatni ładunek jest za słabe, aby spowodować obserwowane rozpraszanie cząstek α. Wyśnienie rozpraszania cząstek α stałoby się możliwe, gdyby przyjąć istnienie silnego pola elektrycznego wewnątrz atomu, czyli gdyby cały dodatni ładunek atomu skupiony był w mikroskopijnie małej przestrzeni w stosunku do rozmiarów całego atomu, czyli w jądrze atomu.

Z teoretycznej analizy liczby cząstek α rozproszonych pod różnymi kątami wynikało, że na podstawie modelu atomu Thomsona nie można wytłumaczyć zachowania cząstek α. Rutherford zaproponował nowy model, zwany jądrowym modelem atomu.

W swoim modelu założył, że cały ładunek dodatni atomu, a w konsekwencji i jego masa, są skoncentrowane w obszarze zwanym jądrem atomu. Dookoła jądra po zamkniętych (eliptycznych, kołowych) orbitach krążą elektrony, tworząc powlokę elektronową atomu.

DOŚWIADCZENIE FRANCKA-HERTZA

W 1914 roku James Franck (1882-1964) i Gustaw Hertz (1887-1970) przeprowadzili eksperyment, w którym potwierdzili istnienie dyskretnych stanów stacjonarnych postulowanych przez teorię Bohra.
    Aby lepiej zrozumieć przebieg tego doświadczenia, należy dokładniej zapoznać się ze strukturą atomów ²⁰²₈₀Hg. Rozpatrzmy poziomy energetyczne elektronów walencyjnych. Poziomy te są poziomami optycznymi co znaczy, że przejście elektronów pomiędzy nimi jest odpowiedzialne za emisję (lub absorpcję) fotonów, które posiadają długości fal leżące w rejonie widzialnego obszaru widma. Popatrzmy na rysunek. Energia elektronu walencyjnego w stanie podstawowym jest równa E_P = -10,42 eV. Energia pierwszego stanu wzbudzonego równa jest E_I = -5,54 eV. Energia, którą trzeba dostarczyć elektronowi, aby przeskoczył ze stanu podstawowego do pierwszego wzbudzonego wynosi więc:

    Elektron po przejściu do stanu wzbudzonego prawie natychmiast wraca do stanu podstawowego emitując przy tym foton o energii około 4,88 eV.
    Jeżeli będziemy teraz mieli naczynie, w którym znajdują się pary rtęci pod niskim ciśnieniem i będziemy przepuszczać przez to naczynie wiązkę powolnych elektronów to możemy zaobserwować następujące zjawisko. Jeśli elektrony przepuszczane przez gaz będą miały energię mniejszą od 4,88 eV to nic nie będzie się działo. Elektrony będą doznawały co prawda zderzeń z cząsteczkami gazu, ale ich energia jest za mała, aby wzbudzić elektrony zewnętrzne (walencyjne) atomów rtęci. Zderzenia te zwane zderzeniami sprężystymi, powodują tylko niewielkie spowolnienie elektronu ponieważ zderzając się z atomem może mu przekazać energię tylko poprzez rozpędzenie go. Masa atomu jednak jest na tyle duża, że w czasie zderzenia z lekkim elektronem rozpędza się on niewiele. Elektron przekazuje mu więc niewiele energii. W czasie przelatywania przez gaz elektron może doznawać wielu takich zderzeń poruszając się torem zygzakowym.

    Jeżeli jednak energia elektronu przekroczy wartość 4,88 eV, to będą mogły zachodzić takie zderzenia, w których atomowi zostanie przekazana taka energia, która spowoduje przeniesienie elektronu walencyjnego ze stanu podstawowego do wzbudzonego (zderzenia niesprężyste). Energia elektronu po takim przekazaniu energii zostaje zmniejszona o 4,88 eV. Elektron w stanie wzbudzonym, po krótkiej chwili (około 10^-8 sekundy), wraca ponownie do stanu podstawowego - następuje emisja fotonu o energii około 4,88 eV. Jeżeli teraz pierwotna energia elektronu jest tylko nieco większa od 4,88 eV elektron może tylko raz zderzyć się w wyżej opisany sposób. Później jego energia będzie mniejsza od 4,88 eV. Jeżeli energia elektronu jest większa 2*4,88 eV mogą zajść dwa takie zderzenia itd. Tak powinno to zachodzić, jeżeli teoria Bohra jest właściwa.
    W 1914 roku Hertz i Franck potwierdzili doświadczalnie istnienie tego zjawiska. Wzięli oni lampę z parami rtęci znajdującymi się w niskim ciśnieniu i w wysokiej temperaturze (około 150⁰C). Wewnątrz lampy znajdowało się źródło elektronów (żarzone uzwojenie). Było ono zasilane z baterii. Mniej więcej w środku lampy znajdowała się siatka, a na końcu anoda. Pomiędzy uzwojeniem, a siatką panowało przyśpieszające elektrony napięcie, które naukowcy mogli zmieniać w zakresie 0-60 V. Między siatką, a anodą istniało natomiast, napięcie hamujące elektrony. Szeregowo w obwód anody włączony został czuły elektrometr. Zwiększając napięcie przyśpieszające wzrastał prąd mierzony przez elektrometr, coraz więcej bowiem elektronów dochodzi do anody. Jednak, gdy napięcie to było w przybliżeniu zwiększane o 5 V, następował spadek prądu!!! Dlaczego tak się dzieje? Okazuje się, że odpowiedzialne jest za to powyżej opisane zjawisko. Jeżeli mamy elektrony o energiach większych od 4,88 eV, mogą się one zderzać z atomami rtęci przekazując im, jak to wcześniej opisałem, energię 4,88 eV. Teraz elektrony te mogą mieć za małą energię, aby dotrzeć do anody, pokonując potencjał hamujący. To tłumaczy pierwszy rejestrowany spadek prądu, przy napięciu około 5 V. Drugi spadek prądu odpowiada natomiast elektronom, które doznają dwóch zderzeń z przekazaniem energii po 4,88 eV. Trzeci spadek odpowiada trzem zderzeniom itd.

    Oprócz tego zmierzyć można długość fal promieniowania emitowanego w czasie doświadczenia przez atomy rtęci. Okazało się, że tak jak wcześniej przewidywano, długość fali odpowiada przejściu elektronu ze stanu wzbudzonego do podstawowego w atomie rtęci, zgodnie z teorią Bohra.

ZASADA HEISENBERGA

Zasada nieoznaczoności podana przez Wernera Heisenberga w 1927 roku.

W zastosowaniu do pomiarów położenia i pędu głosi ona, że:

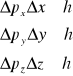
Tak, więc żadna składowa ruchu nie może być określona z nieograniczona dokładnością.

Gdyby wyżej przytoczone iloczyny były równe zeru, a nie h, byłyby słuszne klasyczne pojęcia dotyczące cząstek i orbit. Byłby wtedy możliwy pomiar pędu i położenia z nieograniczoną dokładnością. Występowanie h oznacza, że pojęcia klasyczne są błędne; wielkość h określa, przy jakich warunkach te pojęcia klasyczne muszą być zastąpione pojęciami kwantowymi.

Zasada nieoznaczoności wyjaśnia nam, jak jest możliwe to, że zarówno światło, jak i materia maja dwoistą, falową-cząstkową naturę. Te dwa aspekty nie mogą jednocześnie ujawniać się w tych samych warunkach doświadczalnych. Jeżeli w doświadczeniu silnie ujawnimy charakter falowy, wtedy jego charakter cząstkowy jest utajony i odwrotnie.

INTERPRETACJA BORNA

Interpretacja ta dotyczy równania funkcji falowej wyprowadzonej przez Sredingera .Dla fali płaskiej rozwiązanie równania ma postać
gdzie
A-stała

Zdaniem Borna kwadrat wartości tej funkcji ψ ² reprezentuje gęstość prawdopodobieństwa znalezienia całej cząstki w danym miejscu. Dodatkowo funkcja falowa musi spełniać warunek: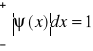

Oznacza to że prawdopodobieństwo znalezienia cząstki w całym możliwym obszarze musi wynosić 1. tzn. musi być unormowana.

Interpretacja Borna jest statystyczną interpretacją funkcji falowej.

NIESKOŃCZONA STUDNIA POTENCJAŁU

Zajmujemy się poruszającą cząstką. Niech ona na swojej drodze napotka na pewna barierę , będzie to bariera potencjału o wysokości U_o i szerokości I.

• x

Jeżeli energia cząstki jest większa niż wysokość bariery (E>Uo) to cząstka bez przeszkód przechodzi ponad barierą ,zaś na odcinku0≤x≤1 zmniejszy ona tylko swoją prędkość. ale na odcinku x>1 znowu ja zwiększy i przyjmuję początkową wartość.

Gdy E < od Uo to cząstka odbija się od bariery i leci w przeciwnym kierunku, gdyż nie może ona przeniknąć prze barierę. Takie rozwiązanie proponuje nam klasyka.

Zaś fizyka kwantowa mówi nam że :

Nawet gdy E>Uo to pojawia się niezerowe prawdopodobieństwo odbicia się cząstki od bariery, i lotu w przeciwnym kierunku. Oprócz tego, gdy E<Uo istnieje niezerowe prawdopodobieństwo tego, że cząstka przeniknie przez barierę i znajdzie się w obszarze x>l.

Takie zachowanie cząstek wynika z równania Schrodingera. Z jego przekształceń wynika że fala w obszarze 1 i2 zachowują się podobnie zaś w 3 jest fala która rozchodzi się w prawo i lewo. Stosunek kwadratów amplitud fali odbitej i padającej określa prawdopodobieństwo odbicia cząstki od bariery potencjału i może być nazwany współczynnikiem odbicia. Stosunek kwadratów modułów amplitud fali przechodzącej i padającej określa prawdopodobieństwo przejścia cząstki przez barierę i nazywamy współczynnikiem transmisji.

Prawdopodobieństwo przejścia cząstki przez barierę potencjału silnie zależy od szerokości bariery i jej przewyższenia ponad E. Jeżeli dla jakiejś bariery współczynnik transmisji =0.01, to w wyniku dwukrotnego zwiększenia szerokości bariery zmniejszy się stukrotnie. Współczynnik transmisji szybko maleje wraz ze wzrostem masy. Przy pokonywaniu bariery potencjału cząstka przechodzi jakby przez tunel ,więc możemy nazwać to zjawisko tunelowym.

LICZBY KWANTOWE ATOMU WODORU

Rozpatrzmy atom wodoru, składający się z nieruchomego jądra o ładunku e i poruszającego się wokół niego elektronu. Energia potencjalna elektronu jest tu równa:
(r - odległość elektronu od jądra). Zatem równanie Schrödingera ma postać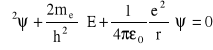
(m_e - masa elektronu). Można udowodnić, że równanie to ma rozwiązania o zadanych własnościach (tzn. jednoznaczne, skończone i ciągłe) w następujących przypadkach: 1) dla dowolnych dodatnich wartości E; 2) dla dyskretnych ujemnych wartości E równych
(n=1,2,3,…). Przypadek E>0 odpowiada sytuacji, gdy elektron przelatuje w pobliżu jądra i oddala się ponownie do nieskończoności. Przypadek E<0 odpowiada elektronowi związanemu z jądrem. Funkcje własne równania na E_n zawierają trzy parametry (n, l i m), będące liczbami całkowitymi:
. Parametr n nazywany główną liczbą kwantową, równy jest numerowi poziomu energii. Parametry l i m są to orbitalna liczba kwantowa i magnetyczna liczba kwantowa, określające moduł momentu pędu i jego rzut na pewien kierunek z. Rozwiązania spełniające warunki standardowe można otrzymać jedynie dla wartości l nie przekraczających n-1. Zatem dla danego n liczba kwantowa l może przyjmować n różnych wartości:
. Dla danego l liczba kwantowa m może przyjmować 2l+1 różnych wartości:
. Energia elektronu zależy tylko od głównej liczby kwantowej n. Zatem każdej wartości własnej energii E_n (oprócz E₁) odpowiada kilka funkcji własnych
, różniących się wartościami liczb kwantowych l i m. Oznacza to, że atom wodoru może mieć jedną i tę samą wartość energii znajdując się w kilku różnych stanach. Stany o jednakowych energiach nazywamy stanami zdegenerowanymi lub zwyrodniałymi, a liczbę różnych stanów o jednakowych wartościach nazywamy krotnością degeneracji. Liczba różnych stanów odpowiadających danemu n jest równa
. A zatem krotność degeneracji poziomów energetycznych atomu wodoru wynosi n².

W związku z istnieniem spinu elektronu powyższy zbiór liczb kwantowych należy uzupełnić, dodając doń liczbę kwantową m_s, która może przyjmować wartości
oraz określa rzut spinu na zadany kierunek. Nazywa się ją spinową liczbą kwantową.

5

p

V

izotermiczne

rozprężanie

adiabatyczne

rozprężanie

izotermiczne

sprężanie

adiabatyczne

sprężanie

A

B

C

D

Y

Y'

Z

Z'

X

X'

1

2

p

V

P = constans

1

2

p

V

1

2

p

V

V = constans

1

2

p

V

Uo

U(x)

E

II

I

III

---