Zestaw A

1.Objaśnij układ wsp. naturalnych; w jaki sposób można połączyć ten układ z pojęciem wysokości? Podstawową osią tego układu jest chwilowa oś obrotu Ziemi ω przechodząca przez punkt S środka masy Ziemi. Płaszczyznę poprowadzoną przez ten pkt, tak aby oś wirowania Ziemi była do niej prostopadła, nazywamy płaszczyzną równika astronomicznego. Płaszczyzna południka astr Greenwich pochodzi z pęku płaszczyzn przechodzących przez kierunek linii pionu obserwatorium Greenwich i jest równoległa do osi ω. Pł.poł.miejsca obs pochodzi z pęku płaszczyzn przechodzących przez kierunek linii pionu w miejscu obs. Jest ona || do osi ω. Kąt jaki tworzy kierunek linii pionu w pkt P z pł równika nazywa się szerokością geograf-astronom ϕ(0-90⁰|
).Kąt dwuścienny utworzony przez pł. południków (Greenwich i P) nazywa się długością geograf-astronom λ (0-360/[E] lub 0-180⁰|
).Kierunek linii pionu w punkcie P(g=gradW_p) można określić w przestrzeni kątami ϕ i λ; g=gradW=-gn=-g. Te kąty ϕ i λ oraz wartość potencjału W stanowią trójkę współrzędnych naturalnych punktu P(ϕ,λ,W).Wartość W_p nie mierzymy bezpośrednio, lecz wyznaczamy ze wzoru C=W₀-W_p=₀ ∫ ^p gdh co ma ścisły związek z pojęciem wysokości. W polu siły ciężkości możemy wyróżnić trzy powierzchnie ϕ=const.,λ=const.i W=const, których przecięcie wyznacza pkt. P.

2.Podaj definicję wysokości ortometrycznych; wyjaśnij czym różnią się wys ortometryczne prawdziwe (Niethammera) od przybliżonych (Helmerta) -Wysokości te oznaczają odległości punktów na fizycznej powierzchni Ziemi od geoidy mierzone wzdłuż linii pionu. Wysokość ortometryczną H^ort otrzymamy dzieląc liczbę geopotencjalną C (wyrażającą różnicę potencjału geoidy W=W₀ i potencjału powierzchni W=W_P przechodzącej przez punkt P) przez przeciętną wartość rzeczywistego przyspieszenia g^- wzdłuż linii pionu od geoidy do punktu P. H^ort = C/g^-. Licznik może być wyznaczany z całki C=W₀-W_p=₀∫^p gdh, za pomocą pomiarów różnic wys.(dh≡Δh), pomiarów przyspieszenia siły ciężkiości.(całkowanie wykonuje się wzdłuż linii pionu pkt P). C= ₀∫^H gdH=H*1/H*₀∫^HgdH=H
; g^-=1/H*₀∫^HgdH; H= -( W_p- W₀)/g^- jest to wyrażenie definiujące wysokość ortometryczną. Realizacja tego wzoru wymaga określenia wartości przeciętnej przyspieszenia siły ciężkości, tymczasem do tej pory stwarza to problem. Wysokości ortometryczne prawdziwe (Niethammera) od przybliżonych (Helmerta) różnią się tym, że Niethammer przedstawił bardzo skrupulatne podejście do wyznaczenia g^-. Zaproponował do jej wyznaczenia wykorzystać redukcje grawimetryczną Poincarego- Praya wziętą w połowie wysokości H/2. Zaś Helmert poczynił pewne uproszczenia, mianowicie zaproponował rezygnację z uciążliwego wyznaczania poprawek terenowych δg_A” i δg_B” (w redukcji Poincarego- Praya) które jako różnice poprawek są z reguły niewielkie, a w terenach płaskich wręcz znikome.

Rys.

3.Redukcja kierunków i długości w odwzorowaniu G-K. Redukcja długości: m=1+y²/2R₁²+y⁴/24R₁⁴-skala odwzorowania; podstawiamy ją do wzoru ds=(1/m)dS i otrzymujemy: s=₀∫^s(1+ y²/2R₁²+y⁴/24R₁⁴)^-1dS; przyjmujemy, że R=R_m czyli śr promieniowi krzywizny środkowego punktu linii S=s(1+(y₁²+y₁y₂+y₂²)/6R_m); taka dokładność wystarcza dla większości przypadków spotykanych w praktyce S≥s; gdy y=0 S=s. Reducje kierunków -kąty(δ) jakie tworzy cięciwa z łukiem krzywej boku trójkąta na płaszczyźnie
; α₁₂=A₁₂-γ₁-δ_{12 ,}α₂₁=A₂₁-γ₂-δ₂₁ to kąty kierunkowe. Wiernokątność odwzorowania zapewnia równość odpowiednich kątów na pow elipsoidy i na płaszczyźnie. Σ kątów wewnętrznych na elipsoidzie=360°+ε, a Σ kątów wew figury płaskiej=360°+δ₁₂+δ₂₁ stąd ε=δ₁₂+δ₂₁; zakładamy, że δ₁₂=δ₂₁→δ₁₂≈ε/2 Powierzchnia trapezu P₁'P₂'O₂'O₁'; P_trapezu=(x₂-x₁)y_m.; y_m=( y₂+y₁)2; Przybliżony wzór δ₁₂≈ε/2=((x₂-x₁)y_m)/(2R_m²).

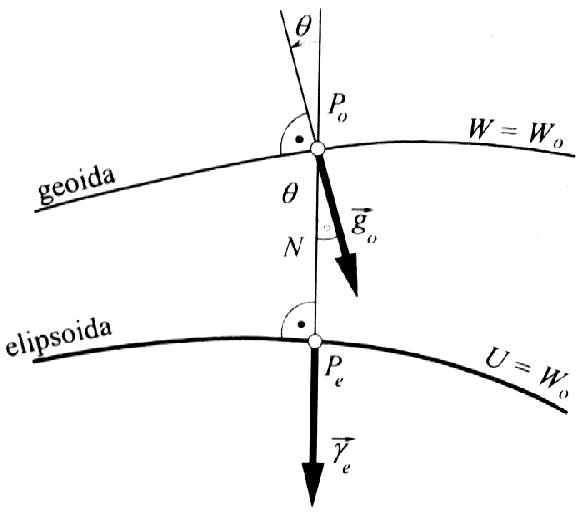
4.Anomalie grawimetryczne; podstawowe równanie geodezji fizycznej -interpretacja; przejście do wzoru Stokesa. Wektor przyspieszenia rzeczywistego na geoidzie w punkcie P₀(g₀=g^→) różni się i wartością i kierunkiem od wektora γ_e^→ w punkcie P_e na elipsoidzie. Punkt P_e powstał poprzez rzut normalny pkt. P₀ z geoidy na elipsoidę. Wektor, będący różnicą g₀^→ i γ_e^→ nazywamy wektorem anomalii grawimetrycznej: Δg=Δg^→=g₀^→-γ_e^→; różnicę modułów wektorów przyspieszenia g₀ na geoidzie i normalnego γ_e nazywamy anomalią grawimetryczną Δg= g₀-γ_e ; kąt θ jaki tworzą kierunki wektorów g₀ i γ_e nazywamy odchyleniem pionu. θ=∠(g₀^→,γ^→_e). Z reguły odchylenia pionu odniesione do geoidy nie przekraczają kilku sekund łuku; maksymalne wartości kąta θ mogą osiągnąć kilkanaście sekund. Są to więc kąty niewielkie.

Powierzchnie, do których odnoszą się obydwa składniki anomalii grawimetrycznej, to geoida i elipsoida ekwipotencjalna. W celu rozwiązania podstawowego zadania geodezji -należy powiązać geometrycznie geoidę z elipsoidą poprzez wyznaczenie odległości obydwu pow. Taką odległość, liczoną od elipsoidy wzdłuż normalnej do tej pow, nazywamy wysokością albo odległością geoidy N. Podstawowe równanie geodezji fiz: Δg=-(∂T/∂n)+(1/γ)(∂γ/∂n)T lub
[gdzie: Δg-anomalia grawimetryczna, γ-przyśpieszenie normalne na geoidzie, n-kierunek normalny, T-potencjał zakłócający, U-potencjał normalny, N-wysokość geoidy względem elipsoidy, δg- właściwa anomalia grawimetryczna(zwana zakłóceniem grawimetrycznym)] wiąże anomalie grawimetryczne z zakłóceniami grawimetrycznymi oraz wysokościami geoidy wzgl elipsoidy. Drugi wyraz prawej strony równania bywa nazywany wyrazem Brunsa. Po zastąpieniu pow elipsoidy ekwipotencjalnej pow kuli o takiej samej objętości, otrzymamy: (4/3)πa²b=(4/3)πR³ ,R=³√a²b; γ≈G(M/R²); (∂γ/∂n)≈(∂γ/∂n)=-(2γ/R); (∂T/∂n)≈(∂T/∂r); Δg≈-(∂T/∂r)-2(T/R); Równanie to jest warunkiem brzegowym, mieszczącym się w tzw. trzecim zagadnieniu brzegowym teorii potencjału na pow ekwipotencjalnej (geoidy), gdyż mamy w nim kombinację liniową potencjału zakłócającego i jego pochodnej w kierunku normalnej do pow ekwipotencjalnej. Wzór Stokesa przedstawia zależność wysokości geoidy nad elipsoidą ekwipotencjalną (N) do anomali grawimetrycznych (Δg) znanych na całej Ziemi: N=R/4πγ_m∫∫_(σ)ΔgS(ψ)dσ; gdzie γ_m-przeciętna wartość przyśpieszenia normalnego siły ciężkości dla całej Ziemi; obszar σ-strefa jednostkowa na którą zrzutowano anomalie w celu przeprowadzenia całkowania; dσ-element powierzchni sfery jednostkowej (o konkretnej wartości przypisanej przez anomalie grawimetryczne); S(ψ)-funkcja Stokesa; ψ-odległość sferyczna punktu (υ',λ') od rozpatrywanego punktu (υ,λ); Δg-anomalia grawimetryczna przyporządkowana elementowi dσ sfery σ. Wzór pozwala na wyznaczenie geoidy z danych grawimetrycznych. ZAŁOŻENIE: potencjał zakłócający ma pole geoidy i w przestrzeni zewnętrznej jest funkcją harmoniczną, żadne masy nie mogą znajdować się ponad geoidą(konieczność wprowadzenia redukcji), elipsoida ekwipotencjalna ma taką samą masę jak geoida; środek elipsoidy jest równy środkowi mas Ziemi, osie głównych momentów bezwładności obu brył pokrywają się.

---