6. Informacja merytoryczna
6.1. Definicja tarcia
Jeżeli dwa ciała:
stykają się ze sobą,
występuje pomiędzy nimi siła wzajemnego oddziaływania o składowej normalnej do po-wierzchni styku różnej od zera,
jedno ciało przemieszcza się względem drugiego z prędkością względną styczną do po-wierzchni kontaktowej -to przemieszczenie względne tych ciał wymaga pewnej siły F stycznej do powierzchni kontaktowej S, niezbędnej do pokonania siły tarcia T (rys. III/4 a).
Przedstawiona sytuacja jest typowa dla procesów obróbki plastycznej, gdzie narzędzie oddziaływuje na powierzchnię przedmiotu kształtowanego pewną siłą normalną, a równocześnie materiał przemieszcza się względem narzędzia w kierunku stycznym do powierzchni kontaktu,
a więc występują siły tarcia (rys. III/4 b).
Pojęcie siły tarcia stosuje się globalnie do całej powierzchni kontaktowej. Lokalnie
(w określonym punkcie) tarcie może być określone przez podanie jednostkowej siły tarcia (naprężenia tarcia) σyx:
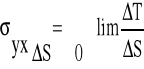
(III.1)
gdzie T jest siłą tarcia działającą na elemencie powierzchni S, kierunek y jest normalny do powierzchni kontaktowej, x jest kierunkiem wektora prędkości materiału v względem narzędzia. Znak „+” lub „-” wybiera się w zależności od zwrotu wektora prędkości v. Średnie naprężenie tarcia tyx określa zależność:
![]()
(III.2)
6.2. Charakterystyka i mechanizmy tarcia w obróbce plastycznej. Czynniki wpływające na siły tarcia
Tarcie występujące podczas obróbki plastycznej jest zjawiskiem bardzo skomplikowanym, ponieważ:
- rzeczywista powierzchnia kontaktowa nie jest równa nominalnej, lecz składa się z wielu mikroobszarów przylegania, których sumaryczna powierzchnia zwiększa się wraz ze wzrostem nacisku, a pozostałe części obydwu powierzchni oddzielone są szczelinami;
- obydwie stykające się powierzchnie nie są idealnie czyste, lecz pokryte tzw. warstwami adsorpcyjnymi o grubości ok. 10-7 - 10-6 mm, które składają się z atomów lub cząsteczek substancji znajdujących się w atmosferze i utrzymywanych na powierzchniach oddziaływaniem sił atomowych [1];
- oprócz warstw adsorpcyjnych na stykających się powierzchniach tworzą się w tempera-turze otoczenia warstwy tlenków o grubościach ok. 10-6 - 10-5 mm [1];
- warstwy tlenkowe i adsorpcyjne tworzą warstwę graniczną, której własności wywierają istotny wpływ na wartości sił tarcia;
- naciski jednostkowe na powierzchniach narzędzi mogą osiągać wartości rzędu 2500 MPa, są więc bardzo duże w porównaniu z typowymi naciskami, występującymi pomiędzy powierzchniami współpracujących ze sobą części maszyn (10 MPa, wyjątkowo 20 - 50 MPa) [3];
- wektory przemieszczeń i prędkości względnych styczne do powierzchni kontaktowej nie są jednakowe na całej powierzchni (np. w pewnych obszarach przemieszczenia względne nie występują wcale);
- występują niejednorodne rozkłady nacisków normalnych i jednostkowych sił tarcia na po-wierzchni styku narzędzia i przedmiotu kształtowanego, a także anizotropia tarcia (zależność naprężenia tarcia σyx od orientacji osi x względem kierunkowego układu śladów obróbki narzędzia kształtującego);
- w pewnych przypadkach może nastąpić przywieranie materiału do narzędzia kształtującego (przemieszczanie cząstek materiału zachodzi wtedy wewnątrz jego objętości, a nie bezpośrednio na powierzchni);
- własności powierzchni narzędzia i przedmiotu odkształcanego kontaktujących się ze sobą mogą ulegać istotnym zmianom - zachodzą procesy zużycia narzędzia i ścierania warstwy materiału, przebiegające na ogół z różną intensywnością w różnych miejscach powierzchni styku (różne naciski jednostkowe!), co wywiera wpływ na stan powierzchni wyrobu;
- podczas nagrzewania materiału do obróbki plastycznej na jego powierzchni tworzą się grube warstwy tlenków (zgorzelina) o różnorodnych własnościach fizycznych i składzie chemicznym zależnym od temperatury i atmosfery pieca grzewczego, przy czym skład chemiczny warstwy wierzchniej materiału również może ulegać zmianie - w efekcie zmiana warunków nagrzewania i temperatury obróbki może spowodować zarówno wzrost, jak i spadek sił tarcia;
- w czasie odkształcania przy dużych naciskach i wysokich prędkościach względnych dyssypacja cieplna pracy tarcia może doprowadzić do lokalnego wzrostu temperatury w mikroobszarach przylegania aż do temperatury topnienia - co prowadzi do spadku sił szczepności
i zmniejszenia tarcia;
- stosuje się różne rodzaje smarów, które w większym lub mniejszym stopniu oddzielają od siebie powierzchnie narzędzia i przedmiotu kształtowanego - wskutek wysokich nacisków jednostkowych utrzymanie ciągłej warstwy smaru nie zawsze jest możliwe, co ma wpływ na występowanie różnorodnych mechanizmów tarcia (tzw. warstwy podsmarne o porowa-tej strukturze, nanoszone metodami chemicznymi na powierzchnię wyrobu, sprzyjają za-chowaniu ciągłej warstwy smaru).
W zależności od warunków panujących na powierzchni kontaktowej rozróżnia się:
- tarcie czyste - przy oddziaływaniu czystych powierzchni;
- tarcie suche - w obecności warstw adsorpcyjnych, tlenków i zanieczyszczeń, bez smaru;
- tarcie płynne - warstwa ośrodka lepkiego całkowicie oddziela od siebie powierzchnie narzędzia kształtującego i przedmiotu odkształcanego;
- tarcie graniczne - warstwa ciekłego smaru oddzielająca współpracujące powierzchnie jest granicznie cienka, a smar jest powierzchniowo aktywny [3];
- tarcie półpłynne - powierzchnie narzędzia kształtującego i przedmiotu odkształcanego są tylko częściowo oddzielone od siebie warstwą smaru (ośrodka lepkiego), gdyż wskutek dużych nacisków jednostkowych warstwa ta uległa w pewnych miejscach przebiciu;
- tarcie półsuche - warstwa smaru występuje jedynie na niewielkich fragmentach po-wierzchni kontaktowej.
Tarcie czyste jest przypadkiem wyidealizowanym i może występować tylko w specjalnych warunkach (np. w próżni). W obróbce plastycznej zazwyczaj występują przypadki tarcia półsuchego i półpłynnego, rzadziej - tarcie płynne i graniczne. Szczegółowy opis mechanizmów tarcia można znaleźć w literaturze (np. [1,2]). W dalszym ciągu podamy jedynie najważniejsze informacje.
Istotne znaczenie dla powstawania sił tarcia suchego ma szczepność mikroobszarów przylegania. Zbliżenie dwóch fragmentów czystych powierzchni metalicznych wskutek działania siły normalnej na odległość oddziaływania sił atomowych powoduje powstanie połączenia metalicznego. Jest to zjawisko adhezji. Na powierzchni kontaktowej tworzy się szereg połączeń (mostków). Sumaryczna powierzchnia mikroobszarów przylegania zależy od rodzaju stykających się materiałów, wartości nacisku jednostkowego i charakterystyk chropowatości obydwu stykających się powierzchni. Siłę tarcia można wyrazić jak następuje:
![]()
(III.3)
gdzie: 0 - średnia wartość naprężenia stycznego, wywołującego ścinanie połączenia metalicznego, Sp - suma powierzchni Si mikroobszarów przylegania. Współczynnik φ wyraża stosunek powierzchni Sp do nominalnej powierzchni kontaktowej S:
![]()
(III.4)
W procesach obróbki plastycznej pod wpływem wysokich nacisków następuje uszkodzenie warstwy granicznej i ułatwiony kontakt czystych powierzchni. Ponadto przedłużenie czasu styku powierzchni powoduje wzrost sił szczepności w mikroobszarach przylegania. Siła tarcia wzrasta więc wraz ze wzrostem nacisku, stopnia odkształcenia oraz powierzchni styku, maleje natomiast, gdy zwiększa się prędkość ruchu względnego. Siła tarcia może ulegać okresowym zmianom, odpowiadającym kolejnym fazom ścinania istniejących połączeń
i tworzenia nowych (drgania przy tarciu).
Jeżeli rzeczywista powierzchnia Sp (wzór (III.3)) narasta proporcjonalnie do wartości siły normalnej N, to (przy założeniu stałej wartości 0) otrzymujemy prawo tarcia suchego (Amontonosa - Coulomba):
![]()
(III.5)
lub, dla jednostkowych sił tarcia:
![]()
(III.6)
gdzie: - współczynnik proporcjonalności, zwany współczynnikiem tarcia, σyy - naprężenie normalne.
Warunki tarcia przy stałym nacisku są inne w momencie rozpoczęcia ruchu, a inne pod-czas jego trwania. W związku z tym rozróżnia się zwykle dwie wartości współczynnika tarcia: statyczną, odnoszącą się do momentu rozpoczęcia poślizgu, oraz kinematyczną - gdy ruch ma już charakter ustalony. Wartości te mogą się znacznie od siebie różnić, jednak dla niektórych materiałów (np. dla porowatych spieków) są bardzo zbliżone, a nawet identyczne.
Jak wiadomo z elementarnego kursu fizyki, współczynnik tarcia jest - dla danej pary materiałów - wielkością stałą (przy małych naciskach i ustalonej charakterystyce chropowatości powierzchni). Wykorzystanie tego stwierdzenia do opisu tarcia w obróbce plastycznej byłoby znacznym uproszczeniem, ze względu na złożoność mechanizmów, warunkujących powstawanie sił tarcia. W związku z tym stosowanie związków (III.5) lub (III.6) wymaga przyjęcia dodatkowych założeń:
- współczynnik należy traktować jako pewien współczynnik proporcjonalności pomiędzy naprężeniem stycznym i normalnym na elemencie powierzchni kontaktowej w konkretnym procesie kształtowania, przy czym jego wartość może się zmieniać w szerokich granicach,
w zależności od wartości lokalnych nacisków jednostkowych, stanu powierzchni, prędkości względnej, sposobu smarowania i rodzaju smaru (w warunkach tarcia półsuchego i półpłynnego), a także temperatury i innych czynników;
- w obliczeniach konkretnych procesów obróbki plastycznej należy stosować adekwatne wartości współczynników tarcia wyznaczane doświadczalnie, przy czym metody badawcze winny uwzględniać rzeczywiste warunki realizacji procesów technologicznych.
Przy bardzo dużych naciskach jednostkowych suma powierzchni mikroobszarów przy-legania staje się bliska nominalnej powierzchni kontaktowej. Związek (III.5) (lub (III.6)) prze-staje obowiązywać, a naprężenie tarcia osiąga wartość maksymalną, uwarunkowaną wytrzymałością połączeń szczepnych na całej powierzchni ( = 1 we wzorze (III.4)). Jeżeli 0 jest mniejsze od granicy plastyczności na ścinanie materiału odkształcanego, to ścięcia połączeń metalicznych następują na powierzchni kontaktowej. W przypadku przeciwnym - materiał przywiera do narzędzia, tworząc narosty. Jest to zjawisko niepożądane, gdyż powoduje złą jakość powierzchni wyrobu. Maksymalna wartość naprężenia tarcia jest więc równa granicy plastyczności na ścinanie materiału kształtowanego: σyx max = k. W warunkach płaskiego stanu odkształcenia:
![]()
(III.7)
zgodnie z warunkiem plastyczności Hubera - Misesa, lub:
![]()
(III.8)
przy warunku Treski. Jest to przypadek stałego tarcia, niezależnego od wartości nacisków jednostkowych σyy. Zamiast (III.6) obowiązuje związek:
![]()
(III.9)
W analizie procesów obróbki plastycznej, związki typu (III.6) lub (III.9) są wykorzystywane jako warunki brzegowe dla naprężeń na powierzchni kontaktowej. Zwraca się uwagę, że równanie (III.9) określa bezpośrednio jedną ze składowych tensora naprężenia, jest więc bardzo dogodne w konkretnych obliczeniach. Może być jednak stosowane tylko w ograniczonym zakresie - gdy naprężenia tarcia są duże w porównaniu z wartością naprężenia uplastyczniającego (obróbka plastyczna na gorąco), lub przy bardzo dużych naciskach jednostkowych (prasowanie płyt o małych wysokościach). Równanie (III.6) podaje jedynie związek pomiędzy składowymi σyx i σyy tensora naprężenia (warunek typu mieszanego), co komplikuje obliczenia. W związku z tym często wykorzystuje się warunek przybliżony:
![]()
(III.10)
który zakłada stałą (niezależną od nacisku normalnego) wartość naprężenia tarcia mniejszą od maksymalnej (0 * 1 jest stałym współczynnikiem). Warunek (III.10) jest dość dobrze spełniony przy odkształcaniu porowatych spieków metali, dla których doświadczalnie stwierdzono brak zależności pomiędzy naprężeniem normalnym i stycznym na powierzchni kontaktowej.
Dla tarcia płynnego obowiązują zależności, wynikające z prawa liniowej lepkości Newtona:
![]()
(III.11)
![]()
(III.12)
gdzie: - współczynnik lepkości dynamicznej smaru, h - grubość warstwy smaru, vx - prędkość materiału względem narzędzia w kierunku x.
Zwraca się uwagę, że:
- bezwzględna wartość siły tarcia jest wprost proporcjonalna do powierzchni kontaktowej
S i prędkości vx oraz odwrotnie proporcjonalna do grubości warstwy smaru (wzór (III.11));
- bezwzględna wartość naprężenia tarcia rośnie ze wzrostem prędkości vx (wzór (III.12)), odwrotnie niż w przypadku tarcia suchego.
Przedstawione wyżej uwagi dotyczą sił tarcia występujących na powierzchniach kontaktowych przedmiotu odkształcanego z narzędziem (tarcie zewnętrzne). Podczas kształtowania plastycznego materiałów rozdrobnionych (np. proszków metali) połączenia szczepne tworzą się nie tylko pomiędzy narzędziem i materiałem obrabianym, ale również wewnątrz odkształcanej objętości (pomiędzy poszczególnymi cząstkami materiału rozdrobnionego), co utrudnia ich względne przemieszczenia. Zjawisko to określa się mianem tarcia wewnętrznego (przez analogię do podobnego zjawiska związanego z niesprężystym zachowaniem się materiałów litych przy małych obciążeniach, powodującego m. in. tłumienie drgań swobodnych, występowanie histerezy sprężystej itp.).
6.3. Wpływ tarcia na przebieg procesów obróbki plastycznej
Praca L siły zewnętrznej F potrzebna do realizacji procesu obróbki plastycznej przy założeniu (III.6) wyraża się wzorem:
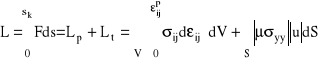
(III.13)
gdzie: Lp - praca odkształceń plastycznych, Lt - praca wykonana przeciwko siłom tarcia,
σij - składowe tensora naprężenia, ![]()
- końowe wartości składowych tensora odkształcenia plastycznego, u - długość wektora przemieszczenia względnego, V - objętość strefy uplastycznionej, sk - całkowite przemieszczenie narzędzia. Udział pracy tarcia Lt w całkowitej pracy L określa współczynnik sprawności procesu t:
![]()
(III.14)
Obecność tarcia w procesach obróbki plastycznej wywołuje następujące skutki:
- ulegają zmianie parametry siłowo - energetyczne: rośnie całkowita praca i moc potrzebna do realizacji procesu, wzrastają więc także siły i naciski jednostkowe na powierzchniach narzędzi, co prowadzi do ich szybszego zużycia;
- występowanie przywierania materiału do narzędzia i tworzenie narostów wpływa na po-gorszenie jakości powierzchni wyrobu;
- dyssypacja cieplna pracy tarcia przy dużych wartościach nacisków jednostkowych oraz prędkości względnych prowadzi do znacznego wzrostu temperatury w obszarach sąsiadujących z powierzchnią kontaktową - może się okazać, że niezbędne jest ograniczenie tych prędkości, a tym samym obniżenie wydajności procesu (inaczej narzędzie ulegnie zniszczeniu lub przedwczesnemu zużyciu, względnie zajdą niepożądane zmiany w strukturze i własnościach warstwy wierzchniej materiału kształtowanego);
- pojawienie się naprężeń stycznych na powierzchni kontaktowej (zmiana warunków brzegowych) powoduje zmianę stanu naprężenia i odkształcenia w całej objętości kształtowanego materiału - w szczególności tarcie jest jedną z przyczyn powstawania niejedno-rodności odkształceń, a więc również niejednorodnych własności materiału oraz niepożądanych deformacji powierzchni swobodnych.
Jak widać, skutki działania tarcia są niepożądane. W związku z tym w procesach obróbki plastycznej dąży się do ograniczenia (zmniejszenia) wartości sił tarcia. Jednak obecność sił tarcia może okazać się niezbędna w realizacji niektórych procesów obróbki plastycznej - np. podczas walcowania pewna siła tarcia jest niezbędna, gdyż umożliwia uchwycenie materiału i nadanie mu określonego ruchu. Bezwzględny wymóg ograniczania sił tarcia może nie dotyczyć pewnych fragmentów powierzchni kształtowanych wyrobów (na których nie występują przemieszczenia względne lub gdy tarcie przenosi część siły potrzebnej do kształtowania).
6.4. Ograniczanie działania sił tarcia
Podstawowym sposobem ograniczania sił tarcia w obróbce plastycznej jest odpowiednie smarowanie. Smar po naniesieniu na powierzchnię przedmiotu odkształcanego lub narzędzia tworzy warstwę oddzielającą częściowo lub całkowicie obydwie powierzchnie. Do pod-stawowych własności smaru zalicza się lepkość i aktywność powierzchniową, które warunkują utrzymywanie się na powierzchni w warunkach wysokich nacisków jednostkowych. Ze względu na dużą różnorodność warunków realizacji procesów obróbki plastycznej nie ma smarów uniwersalnych. Każdy proces wymaga odrębnego podejścia do problemu smarowania i wykorzystania odpowiednich substancji smarujących. W chwili obecnej istnieją wyspecjalizowane firmy, zwykle związane z przemysłem naftowym, które produkują odpowiednie smary z prze-znaczeniem do konkretnych procesów, gatunków kształtowanych materiałów, zakresów temperatur itp.
Różnorodność wymagań stawianych smarom można objaśnić na przykładach:
- w obróbce plastycznej na zimno - zwłaszcza przy wysokich naciskach jednostkowych i dużych prędkościach względnych - smar, oprócz swej podstawowej roli, jaką jest zmniejszenie tarcia, winien również intensywnie chłodzić narzędzie i materiał kształtowany (działanie chłodząco - smarujące) - oprócz odpowiedniej lepkości i aktywności powierzchniowej wymagana jest więc duża pojemność cieplna;
- współczynnik lepkości dynamicznej substancji smarującej winien być odpowiednio dobrany do wartości nacisków jednostkowych (a więc rodzaju kształtowanego materiału) oraz prędkości względnej - im większe naciski, tym większa winna być lepkość smaru; podwyższenie współczynnika lepkości, podobnie jak wzrost prędkości względnej, zwiększa wprawdzie tarcie, jednak przy dużych prędkościach rośnie grubość warstwy smaru, co pozwala na utrzymanie sił tarcia na odpowiednio niskim poziomie (patrz wzór (III.11));
- w obróbce plastycznej na gorąco - zwłaszcza gdy czas zetknięcia się narzędzia z przed-miotem obrabianym jest duży - istotna jest przede wszystkim odporność smaru na tempe-raturę (istnieje niewiele substancji, które mogą spełniać rolę smaru
w temperaturach rzędu 1000 oC) oraz niskie przewodnictwo cieplne, ze względu na zabezpieczenie narzędzia przed przegrzaniem.
We wszystkich przypadkach smar powinien mieć następujące cechy:
- łatwość nanoszenia na powierzchnie kształtowanego przedmiotu i narzędzia,
- chemiczną pasywność względem materiału kształtowanego i materiału narzędzia,
- nieszkodliwość dla pracowników i środowiska naturalnego,
- łatwość usuwania z powierzchni po zakończeniu obróbki.
Stosuje się następujące rodzaje smarów:
- smary płynne: oleje mineralne i roślinne oraz emulsje (oleje z dodatkiem wody) jako ośrodki chłodząco - smarujące, oleje o podwyższonej lepkości z dodatkiem parafiny lub stearyny, oleje z dodatkiem substancji powierzchniowo-aktywnych (np, związków chloru);
- smary proszkowe: mydła w postaci proszku lub płatków, grafit, dwusiarczek molibdenu (dwie ostatnie substancje stosuje się również jako dodatki do smarów płynnych);
- szkło (w postaci proszku lub waty szklanej), stosowane w wysokich temperaturach [3].
Stworzenie warunków tarcia płynnego można osiągnąć przy zastosowaniu podawania ciekłego smaru do strefy oddziaływania narzędzia i przedmiotu kształtowanego pod ciśnieniem (smarowanie hydrostatyczne), lub poprzez specjalne ukształtowanie profilu narzędzia: smar jest zabierany przez przemieszczający się materiał i wprowadzany do szczeliny o malejącej stopniowo grubości, przez co jego ciśnienie wzrasta (hydrodynamiczne podawanie smaru).
Utrzymanie smaru na powierzchni przy wysokich naciskach jednostkowych, oprócz odpowiednich własności smaru, wymaga czasem specjalnych zabiegów przygotowania po-wierzchni kształtowanego wyrobu. Jednym ze sposobów jest wspomniane już nanoszenie metodami chemicznymi warstw podsmarnych (np. fosforanów lub szczawianów na powierzchnie stalowe). Warstwy podsmarne powinny mieć porowatą strukturę, sprzyjającą utrzymaniu smaru. Innym sposobem obniżenia tarcia jest stosowanie tzw. rozdzielaczy. Sposób ten polega na pokrywaniu powierzchni kształtowanego materiału cienką warstwą metalu plastycznego (miedź, ołów), który tworzy z materiałem narzędzia słabe połączenia szczepne.
Smary nanosi się różnymi sposobami, zarówno przed, jak i w czasie obróbki, wyłącznie na te fragmenty powierzchni materiału lub narzędzia, na których działanie sił tarcia wpływa niekorzystnie na przebieg procesu kształtowania. Fragmenty powierzchni, na których tarcie nie występuje (np. nie ma przemieszczeń względnych), względnie przenosi część sił kształtowania, pozostawia się nie smarowane.
W przypadku kształtowania wyrobów z materiałów rozdrobnionych (np. proszków metali) istotne jest zmniejszenie sił tarcia działających pomiędzy poszczególnymi cząstkami materiału. Można to osiągnąć przez zastosowanie środka poślizgowego, który należy zmieszać
z materiałem rozdrobnionym przed procesem kształtowania. Dla proszków metali często stosowanym środkiem poślizgowym jest stearynian cynku.
Dla ograniczenia sił tarcia istotna jest charakterystyka chropowatości powierzchni oraz gatunek i twardość materiału narzędzia. Gładka powierzchnia i wysoka twardość materiału narzędziowego sprzyja zmniejszeniu sił tarcia.
Obniżenie sił tarcia można również osiągnąć drogą pośrednią - obniżenia nacisków jednostkowych. Uzyskuje się w to poprzez zmianę panującego stanu naprężenia. Na przykład, w procesach walcowania i ciągnienia stosuje się tzw. naciąg i przeciwciąg (dodatkowe rozciąganie walcowanego pasma lub ciągnionego drutu czy pręta). Część pracy odkształcenia plastycznego jest wtedy wykonana przez naprężenia rozciągające, co powoduje zmniejszenie naprężeń normalnych na powierzchni kontaktowej, a więc spadek sił tarcia.
Eliminację sił tarcia na pewnych fragmentach powierzchni kontaktowej można uzyskać przez zastosowanie odpowiedniej kinematyki procesu. Przykładowo, podczas wyciskania z nieruchomym wsadem, możliwość przemieszczania się wsadu względem pojemnika, a więc również siła tarcia materiału o jego ścianki zostaje znacznie ograniczona.
Zmniejszenie sił tarcia obserwuje się również podczas procesów dynamicznych, gdy prędkości względne są duże (krótki czas styku narzędzia z materiałem kształtowanym), a także w procesach pulsacyjnych, realizowanych z częstotliwością pulsacji siły lub przemieszczenia rzędu kilkuset Hz (bądź też z częstotliwościami ultradźwiękowymi).
Na zakończenie dodamy, że - jeżeli tylko jest to możliwe - należy dążyć do zamiany tarcia ślizgowego na toczne (np. zamiast klasycznego ciągnienia stosuje się ciągnienie po-między swobodnie obracającymi się walcami, wygniatanie gwintów wewnętrznych o dużych średnicach można zastąpić walcowaniem głowicami rolkowymi itp). Pozwala to na obniżenie sił
i momentów potrzebnych do realizacji procesów oraz umożliwia stosowanie wysokich prędkości obróbki, a więc podwyższenie wydajności. Niebezpieczeństwo wystąpienia wysokich temperatur w strefie kontaktu narzędzia i przedmiotu obrabianego jest w przypadku tarcia tocznego znacznie ograniczone, a narzędzie zachowuje wysoką trwałość.
6.5. Doświadczalne metody wyznaczania współczynnika tarcia
Współczynnik tarcia można wyznaczyć:
- wykonując niezależne pomiary sił: stycznej i normalnej, wchodzących do wzoru (III.5), lub określając stosunek tych sił, bez mierzenia ich wartości;
- badając kształt oraz wymiary odkształcanych próbek i porównując je z wartościami wyznaczonymi teoretycznie przy założonych z góry wartościach współczynnika tarcia (wykorzystuje się wpływ tarcia na stan odkształcenia).
6.5.1. Wyznaczanie współczynnika tarcia przy walcowaniu
W metodzie zaproponowanej przez I. M. Pawłowa mierzy się siłę nacisku N działającą na walec, siłę powstrzymującą uchwycenie materiału F oraz kąt chwytu (rys. III/5 a). Z warunków równowagi walca (rys. III/5 b) i materiału (rys. III/5 c) wynika, że:
![]()
![]()
(III.15)
Dzieląc stronami równania (III.15) i wykonując odpowiednie przekształcenia otrzymujemy:
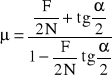
(III.16)
Siły N i F winny być zmierzone w początkowym stadium poślizgu walców, gdyż inaczej powierzchnia materiału ulegnie starciu i zmieni się współczynnik tarcia.
Inny sposób polega na wykorzystaniu warunku chwytu (rys. III/6). Z warunku równowagi sił działających na materiał wynika:
![]()
(III.17)
czyli:
![]()
(III.18)
gdzie max jest graniczną wartością kąta chwytu: jeżeli max - materiał jest wciągany pomiędzy walce, gdy max - uchwycenie materiału nie nastąpi. Wykorzystując (III.18) oraz związki geometryczne (rys. III/6):
![]()
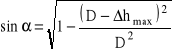
(III.19)
otrzymuje się:

(III.20)
W celu wyznaczenia współczynnika tarcia wystarczy więc określić graniczną wartość gniotu bezwzględnego hmax. W przedstawionej metodzie nie ma potrzeby wyznaczania wartości sił: normalnej i stycznej (mierzy się ich stosunek, równy współczynnikowi tarcia).
6.5.2. Wyznaczanie współczynnika tarcia przy kuciu lub prasowaniu
Przy wyznaczaniu współczynnika tarcia podczas kucia i prasowania wykorzystuje się najczęściej:
- metodę stożków (Siebela i Pompa),
- metodę spęczania klina (I. J. Tarnowskiego),
- metodę niezależnego pomiaru sił: normalnej i stycznej,
- metodę spęczania pierścieni.
Wyznaczone powyższymi metodami wartości współczynnika tarcia *mogą być również wykorzystane w analizie innych procesów kształtowania objętościowego.
Metoda stożków (rys. III/7 a) polega na spęczaniu walcowych próbek ze stożkowymi wybraniami w powierzchniach czołowych za pomocą stożkowych kowadeł z odpowiednio dopasowanymi kątami nachylenia tworzących. W zależności od kąta otrzymujemy trzy przypadki odkształcania się próbki (rys. III/7 b, c, d):
b) Nx Tx, tg ,
c) Nx = Tx, = tg ,
d) Nx Tx, tg .
Określenie współczynnika tacia polega więc na dobraniu takiego kąta , dla którego próbka zachowuje kształt walcowy. Nie ma potrzeby wyznaczania sił T i N.
W metodzie spęczania klina na boczną powierzchnię próbki nanosi się szereg równo-ległych rys i mierzy się odległości x1 i x2 rysy, która nie uległa deformacji (przekroju neutralnego) od końców próbki (rys. III/8). Ponieważ klin jest w równowadze, więc suma rzutów wszystkich sił na oś poziomą wynosi zero, co daje:
![]()
(III.21)
Przy założeniu, że siły N1 i N2 są proporcjonalne do odpowiednich długości l1 i l2, a zatem również do x1 i x2, można związek (III.21) napisać w postaci:
![]()
(III.22)
Ostatecznie:
![]()
(III.23)
W metodzie niezależnego pomiaru sił (rys. III/9) próbkę ściska się pomiędzy dwoma kowadłami 2 znaną siłą F i mierzy się równocześnie siłę P działającą na uchwyt 3, która wywołuje ruch próbki 1 względem kowadeł. Współczynnik tarcia wyznacza się ze wzoru:
![]()
(III.24)
Można badać wpływ wielkości siły normalnej na współczynnik tarcia oraz różnice statycznych
i kinematycznych wartości współczynnika tarcia. Przy dużych naciskach wyznaczone wartości współczynników są wartościami średnimi dla całej powierzchni kontaktowej.
Schemat spęczania pierścienia pokazano na rys. III/10. Przy małym tarciu pierścień ulega poszerzeniu, a jego wewnętrzna średnica po spęczaniu d1 d0 (b). Przy dużych siłach tarcia na pewnej średnicy materiał przywiera do narzędzia, a w związku z tym część materiału przemieszcza się do wewnątrz, a część - na zewnątrz (c). Średnica wewnętrzna może więc zmaleć (lub, w granicznym przypadku, nie zmienić się). Metoda bardzo dobrze nadaje się do porównawczych badań tarcia w różnych warunkach, np. przy różnych smarach, różnych chropowatościach powierzchni narzędzi itp. Jeżeli nie jest potrzebna znajomość wartości współ-czynników tarcia, to wystarczy porównać średnice wewnętrzne pierścieni po spęczaniu
w różnych warunkach, przy czym wymiary początkowe badanych pierścieni oraz stopień odkształcenia muszą być identyczne. Im większą średnicę wewnętrzna pierścienia otrzymuje się po spęczaniu, tym mniejsze były siły tarcia. Wyznaczanie liczbowych wartości współczynników tarcia polega na porównaniu rzeczywistych wymiarów pierścieni po spęczaniu (średnicy wewnętrznej i wysokości) z rozwiązaniem teoretycznym, które opisuje wpływ tarcia na kształt spęczanego pierścienia. Rozwiązanie takie otrzymuje się numerycznie - nie można więc podać zależności typu = f(h1/h0,d1/d0) w postaci zamkniętej. W związku z tym wykorzystuje się odpowiednie nomogramy lub wykresy, z których - dla znanych wymiarów h0, d0 oraz h1 i d1 - można odczytać wartość współczynnika tarcia (rys. III/11).
Rys. III/10. Schemat spęczania pierścienia (a) i wymiary próbek po spęczaniu dla różnych wartości współczynnika tarcia (b, c): d1 > d0, d2 < d0, 2 > 1
6.5.3. Wyznaczanie współczynnika tarcia w procesach tłoczenia
Współczynnik tarcia można wyznaczyć w próbie rozciągania paska blachy podpartego stemplem z zakończeniem walcowym przez pomiar sił F1 i F0 (rys. III/12). Z warunku równowagi elementu próbki wynika:
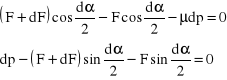
(III.25)
gdzie dp oznacza nacisk stempla na powierzchni dS. Przyjmując, że: ![]()
, po wykonaniu odpowiednich przekształceń pominięciu małej wartości wyższego rzędu ![]()
otrzymujemy:
![]()
(III.26)
Całkowanie (III.26) przy warunku brzegowym: dla = 0, F = F0 daje:
![]()
(III.27)
oraz, dla = φ:
![]()
(III.28)
Ostatecznie:
![]()
(III.29)
6.5.4. Badania tarcia w procesach prasowania proszków lub spieków w matrycach zam-kniętych
Podczas prasowania proszku lub materiału spiekanego w matrycy zamkniętej (rys. III/13) składającej się z dwóch połówek 3 i 4 mierzy się niezależnie siły F1, F2 lub Fm oraz siłę boczną Pb działające odpowiednio na: stempel górny 1, stempel dolny (korek) 2, matrycę (od dołu) i połówkę matrycy. Sumaryczną siłę tarcia na ściankach matrycy wyznacza się z zależności:
![]()
(III.30)
Średnią jednostkową siłę tarcia określa związek:
![]()
(III.31)
gdzie: d - średnica otworu matrycy h - wysokość prasowanej próbki. Średnią wartość współ-czynnika tarcia można oszacować w przybliżeniu jak następuje:
![]()
(III.32)
7. Literatura
1. W. Dobrucki: Zarys obróbki plastycznej metali. Wyd. „Śląsk”, Katowice 1975
2. M. Gieżyńska: Tarcie, zużycie i smarowanie w obróbce plastycznej metali. WNT, Warszawa 1982
3. M. Morawiecki, L. Sadok, E. Wosiek: Przeróbka plastyczna. Podstawy teoretyczne. Wyd. „Śląsk”, Katowice 1986
v
σyx
T
N
N
T
S
v
F
a)
σyy(x)
y
N
x
σyx(x)
σyy
dS
b)
S
Rys. III/4. Schemat działania sił tarcia:
a) podczas przesuwania ciała po powierzchni: N - składowa normalna siły nacisku, T - siła tarcia, F - siła wywołująca przemieszczenie, v - wektor prędkości względnej, S - nominalna powierzchnia styku, T - siła tarcia działająca na elemencie powierzchni S; b) przy prasowaniu płyty pomiędzy dwoma kowadłami:
σyx - jednostkowa siła tarcia (naprężenie tarcia), σyy - naprężenie normalne
R
F/2
T=R
N
F
N
N
/2
T
T=R
R
/2
/2
a)
b)
c)
T
F
Rys. III/5. Wyznaczanie współczynnika tarcia metodą Pawłowa: a) schemat,
b) układ sił działających na walec,
c) układ sił działających na połowę pasma;
siły F i N są mierzone niezależnie za pomocą dwóch dynamometrów
h max /2
max
R
T = R
Rys. III/6. Schemat sił działających na pasmo materiału w momencie chwytu
D
(D-h max)/2
N
T=N
Tx
Nx
a)
b)
d)
c)
P
Rys. III/7. Schemat metody stożków (a) oraz poszczególne przypadki dkształcania się próbek (b, c, d)
F
l1
l2
N2
N1
T1
T2
x1
x2
P
2
3
1
Rys. III/8. Schemat wyznaczania współczynnika tarcia metodą spęczania próbki klinowej
Rys. III/9. Schemat wyznaczania współczynnika tarcia na podstawie niezależnego pomiaru sił:
1 - próbka, 2 - kowadło, 3 - uchwyt do przesuwania próbki
d0
F
h0
h
d1
d2
1
2
D0
a)
b)
c)
d1 [mm]
h [mm]
Rys.III/11. Wykres do wyznaczania wartości współczynników tarcia na podstawie wymiarów spęczanych pierścieni (dla wymiarów początkowych: D0 = 20 mm, d0 = 10 mm, h0 = 7 mm)
F
ၪ
dP
dP
F+dF
d/2
F0
F1
Rys. III/12. Schemat próby rozciągania paska blachy podpartej walcowym stemplem (a) i układ sił działających na element blachy (b); ၪ - kąt opasania
T1
T2
Pb
Pb
F1
F2
Fm/2
Fm/2
1
3
4
2
Rys. III/13. Schemat badania tarcia podczas prasowania proszku w dzielonej matrycy:
1 - stempel górny,
2 - stempel dolny (korek),
3, 4 - połówki dzielonej matrycy
Wyszukiwarka
Podobne podstrony:
PG cw3
cw3
cw3 rezystancja id 123348 Nieznany
cw3 odp
cw3 2014 notatki
LA cw3
cw3 9
CW3 INST
korespondencja polecenia, Weterynaria Lublin, INFORMATYKA, cw3, cw2
SK-cw3 2h Konfigurowanie sieci WLAN, Sieci Komputerowe
szymikowski OPTO cw3 (ndkn)
ćw3 zmk
Ćw3 jak w kserówkach
metody cw3
Cw3 Diody
Metrologia cw3
ćw3 lokalizacja Zuzia3
więcej podobnych podstron