Model 3

Model optymalnego rozdziału zastępowanych zasobów.

Charakterystyka modelu:

Model ten stosowany jest wówczas, gdy istnieje możliwość wykorzystania różnych produktów:

1. na różnych wzajemnie zastępowanych miejscach pracy (przy różnych pracochłonnościach jednostkowych na każdym miejscu pracy);

2. z różnych wzajemnie zastępowanych surowców (przy różnym jednostkowym zużyciu surowca);

Pojęcie produktów i miejsc pracy jest bardzo szerokie. Produktami mogą być np. pręty stalowe o różnych przekrojach, a miejscami ich produkcji różne walcarki. Produktami mogą być również oleje, a miejscami ich produkcji różne rafinerie.

Głównie model ten znajduje zastosowanie w gałęziach produkcji, w których nie ma istotnych różnic w technologii wytwarzania różnych asortymentów jak np.: odlewnie, walcownie, kuźnie, przemysł papierniczy, włókienniczy, gumowy, materiałów budowlanych itp..

Rozwiązanie takiego modelu sprowadza się do takiego rozdziału zasobów (miejsc pracy, surowców) do określonych prac, który:

1. zapewnia uzyskanie największego efektu (zysku wielkości produkcji) - przy określonym czasie pracy lub posiadającej ilości surowców;

2. przy wytworzeniu określonej ilości produktu zapewnia minimalne zużycie czasu i surowców, a więc minimalne koszty ich wytwarzania.

Przykład:

Trzy różne produkty A, B, C, mogą być wytwarzane na trzech maszynach. Poniższa tabela zawiera parametry niezbędne do obliczeń. Należy tak zaplanować pracę maszyn aby osiągnąć maksymalny zysk.

Maszyny	Wydajność (szt./godz.)			Koszty własne (zł/szt.)			Cena jednostkowa produkcji (zł/szt.)	Plan produkcji (szt.)
Produkty	I	II	III	I	II	III
A	1	2	1,5	3	5	3	7	100
B	3	6	4,5	4	5	2	8	50
C	5	10	7,5	2	1	3	6	80
	30	20	40

Zmienne strategiczne:

x_AI, x_AII, x_AIII, x_BI, x_BII, x_BIII, x_CI, x_CII, x_CIII - ilość produkowanych wyrobów A, B,C na poszczególnych maszynach.

Funkcja celu:

Z_max = (7 - 3)x_AI + (7 - 5)x_AII + (7 - 3)x_AIII + (8 - 4)x_BI + (8 - 5)xB_II + (8 - 2)_BIII + (6 - 2)x_CI + (6 - 1)x_CII + (6 - 3)x_CIII

Współczynniki przy zmiennych określają zysk jednostkowy wyrobu w zł./szt., który stanowi różnicę między ceną produktu a kosztem jego wytwarzania.

Ograniczenia:

Ze względu na dysponowany fundusz czasu pracy maszyn:

Ze względu na plan produkcji:

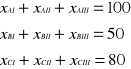
Obliczenia wyżej podanego modelu nie doprowadziły do otrzymania rozwiązania. Okazało się, że taki model jest sprzeczny. Sprzeczność modelu wynika stąd, że dla zaplanowanych ilości wyrobów dysponowany fundusz czasu pracy maszyn jest niewystarczający. Konieczne w takim przypadku jest:

• Zwiększenie funduszu czasu pracy maszyn;

• Przy niezmienionych zdolnościach produkcyjnych maszyn zgoda na mniejsza niż planowaną wielkość produkcji wyrobów.

W obliczeniach przyjęto drugą z powyższych możliwości, spowodowało to konieczność zmiany trzech ostatnich równań na nierówności typu „≤”.

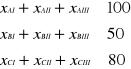
Dla tak zmodyfikowanego problemu otrzymano następujące rozwiązania:

• aby otrzymać maksymalny zysk 1041 zł. należy wytwarzać produkty:

A - na maszynie I w ilości 30 sztuk.

na maszynie II w ilości 24 sztuk

na maszynie III w ilości 43 sztuk

Czyli łącznie należy produkować 97 sztuk wyrobu A.

B - na maszynie III w ilości 50 sztuk

C - na maszynie II w ilości 80 sztuk

Zatem:

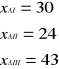
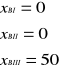
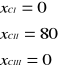
Z rozwiązania wynika, że brak jest dostatecznej zdolności produkcyjnej do wytworzenia trzech sztuk wyrobu A. Natomiast wykorzystanie zasobów czasu pracy maszyn jest pełne.

---