Gołąbecki Mateusz
Rok I, Gr. 2
Budownictwo
Ćwiczenie 67
Wyznaczanie długości fali światła za pomocą siatki dyfrakcyjnej.
Wprowadzenie:
Celem ćwiczenia było wyznaczenie długości fali światła za pomocą siatki dyfrakcyjnej.
Etap pierwszy polegał na wyznaczeniu stałej siatki d, potrzebnej w etapie drugim do wyznaczenia długości fali λ.
W doświadczeniu posługiwaliśmy się zestawem pomiarowym takim jak na rysunku :
Siatka dyfrakcyjna ekran
Wykonanie ćwiczenia :
Siatkę dyfrakcyjną ustawiliśmy równolegle do ekranu . Na początku wyznaczamy stałą siatki dyfrakcyjnej d .
Włączamy źródło światła o znanej długości fali (światło lasera o λl = 632,8nm. Odczytujemy położenie linii widmowych dla trzech rzędów po lewej i prawej stronie szczeliny. Następnie obliczamy sinus kąta ugięcia ze wzoru sinαn = xn / (xn2 + l 2),
z czego otrzymujemy:
sinα1 = 0,056/[(0,056)2 +(0,9) 2 ] = 0,056/ (0,0031 + 0,81) = 0,056/0,8131= 0,0689, zatem:
α1 = 3°56';
sinα2 = 0,115/[(0,115)2 +(0,9) 2 ] = 0,115/ (0,0132 + 0,81) = 0,115/0,9432 = 0,1219, zatem:
α2 = 7°00';
sinα3 = 0,174 /[(0,174)2 +(0,9) 2 ] = 0,174/ (0,0302 + 0,81) =0,174/0,8402 = 0,2071, zatem:
α3 = 12°00'.
Na podstawie wzoru : dn = nλ / sinαn, obliczam stałą siatki dn :
dn1= 1x632,8 / 0,056 = 11300nm
dn2 = 2x632,8 / 0,115 = 11005,22nm
dn3 = 3x632,8 / 0,174 = 10910,35nm
średnia stała siatki d : d = (dn1 +dn2 +dn3)/3
d = (11300 + 11005,22 + 10910,35) / 3 = 11071,86nm
Drugi etap polegał na wyznaczeniu długości fali świetlnej λ dla kolorów: niebieskiego, zielonego i żółtego
Wykonanie ćwiczenia:
Za szczeliną ekranu ustawiliśmy lampę rtęciową. Tak jak poprzednio zapisywaliśmy położenia rzędów widmowych: na lewo od szczeliny al i na prawo ap
Odczyt przeprowadzam dla trzech rzędów intensywnie świecących prążków barwy: niebieskiej, zielonej i żółtej.
Obliczamy dla każdego rzędu średnią odległość prążka od szczeliny, korzystając ze wzoru an =(al +ap) / 2.
Obliczamy sinαn (kąt ugięcia) ze wzoru sinαn = an / (an2 + l 2).
Niebieski:
sinαn1 = 0,035 / (0,0012 + 0,81) = 0,035 / 0,8112 = 0,043, zatem αn1 = 2°27';
sinαn2 = 0,075 / (0,0056 + 0,81) = 0,075 / 0,8156 = 0,092, zatem αn2 = 5°18';
sinαn3 = 0,115 / (0,0132 + 0,81) = 0,115 / 0,8232 = 0,140, zatem αn3 = 8°05'.
Zielony:
sinαn1 = 0,050 / (0,0025 + 0,81) = 0,046 / 0,8125 = 0,057, zatem αn1 = 3°17';
sinαn2 = 0,100 / (0,0100 + 0,81) = 0,100 / 0,8200 = 0,122, zatem αn2 = 7°00'
sinαn3 = 0,145 / (0,0210 + 0,81) = 0,145 / 0,8310 = 0,175, zatem αn3 = 10°05'.
Żółty:
sinαn1 = 0,060 / (0,0036 + 0,81) = 0,060 / 0,8136 = 0,073 αn1 = 4°12';
sinαn2 = 0,120 / (0,0144 + 0,81) = 0,120 / 0,8244 = 0,146 αn2 = 8°24';
sinαn3 = 0,170 / (0,0289 + 0,81) = 0,170 / 0,8389 = 0,203 αn3 = 11°42'.
Obliczam długość fali dla barwy niebieskiej:
λn = d sinαn / n
λn1 = 11071,86x0,043 / 1 = 476,09nm;
λn2 = 11071,86x0,092 / 2 = 509,31nm;
λn3 = 11071,86x0,140 / 3 = 516,69nm;
wartość średnia to:
λ = (λn1 + λn2 + λn3) /3 = (476,09 + 509,31 + 516,69) / 3 = 500,70nm.
Obliczam długość fali dla światła zielonego:
λn = d sinαn / n
λn1 = 11071,86x0,057 / 1 = 631,10nm;
λn2 = 11071,86x0,122 / 2 = 675,38nm;
λn3 = 11071,86x0,175 / 3 = 645,81nm;
wartość średnia to:
λ = (λn1 + λn2 + λn3) /3 =(631,10 + 675,38 + 645,81) / 3 = 650,76nm.
Obliczam długość fali dla światła żółtego:
λn = d sinαn / n
λn1 = 11071,86x0,073 / 1 = 808,25nm;
λn2 = 11071,86x0,146 / 2 = 808,25nm;
λn3 = 11071,86x0,203 / 3 = 749,20nm;
wartość średnia to:
λ = (λn1 + λn2 + λn3) /3 =(808,25 + 808,25 + 749,20) / 3 = 788,57nm.
Rachunek błędu:
I Błąd pomiaru długości fali λ3 dla prążka rzędu 3:
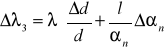
, gdzie ![]()
i 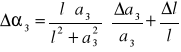
oraz ![]()
i Δl = 5mm.
a)Dla niebieskiego:
Δd = |11071,86 - 11300| = 228,14nm;
![]()
;
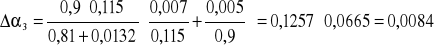
;
zatem: 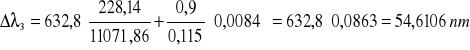
;
b)Dla zielonego:
Δd = |11071,86 - 11005,22| = 66,64nm;
![]()
;
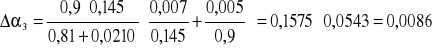
;
zatem: 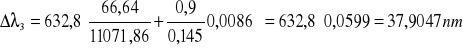
;
c)Dla żółtego:
Δd = |11071,86 - 10910,35| = 161,51nm;
![]()
;
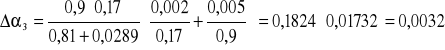
;
zatem: 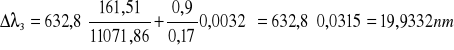
.
Wyszukiwarka
Podobne podstrony:
Ćwiczenie 53, Ćwiczenie 53, Gołąbecki Mateusz
Ćwiczenie 53, Ćwiczenie 53, Gołąbecki Mateusz
cw2 Golabek, Ćwiczenia - dr Gołąbek
29 67 77, ćwiczenie 67 prawo Faradaya
29 67 77, ćwiczenie 67 prawo Faradaya
Ćwiczenie 67, Ćwiczenie 67 (5), Małgorzata Papierowska
Ćwiczenie 67, Ćwiczenie 67 (3), Monika Wojakowska
ćwiczenie 67, Tomasz Zaborny, gr
67-siatka dyfrakcyjna3, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria
67 NW 07 Przyrzady do cwiczen
67 NW 08 Przyrzady do cwiczen
Ćwiczenie nr 67
67 NW 08 Przyrzady do cwiczen
67 NW 07 Przyrzady do cwiczen
3 ćwiczenia BADANIE asfaltów
Ćwiczenie7
więcej podobnych podstron