Nazwisko BŁAZIK		WYŻSZA SZKOŁA PEDAGOGICZNA w Rzeszowie
Imię KATARZYNA		Wykonano		Oddano
Kierunek Fizyka z informatyką II		13-02-2001	Podpis	20-02-2001	Podpis
Grupa laboratoryjna: VIII
Nr ćwiczenia 67	Temat ćwiczenia Wyznaczanie długości fali świetlnej za pomocą siatki dyfrakcyjnej

Część teoretyczna

Dyfrakcja

Zjawisko dyfrakcji (ugięcia) odkrył Grimaldi (XVII w). Polega ono na uginaniu się promieni świetlnych przechodzących w pobliżu przeszkody (np. brzeg szczeliny).

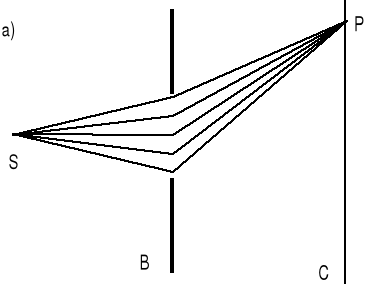
Rysunek (a) pokazuje ogólnie na czym polega dyfrakcja.

Fala ze źródła S pada na szczelinę B i przechodzące przez otwór pada na ekran C. Natężenie w punkcie P można obliczyć dodając do siebie wszystkie zaburzenia falowe. Te zaburzenia falowe mają różne amplitudy i fazy ponieważ:

• elementarne źródła Huyghensa (punkty w szczelinie) są w różnych odległościach od punktu P.

• światło opuszcza te punkty pod różnymi kątami.

Taka sytuacja gdy fale opuszczające otwór nie są płaskie (promienie nie są równoległe) pojawia się gdy źródło fal S i ekran (C), na którym powstaje obraz znajdują się w skończonej odległości od ekranu ze szczeliną (B). Taki przypadek nosi nazwę dyfrakcji Fresnela. Obliczenia natężeń światła są w tej sytuacji trudne.

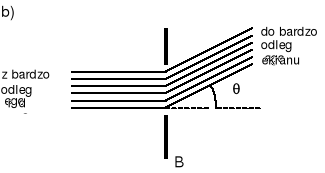
Całość upraszcza się, gdy źródło S i ekran C odsuniemy na bardzo duże odległości od otworu uginającego. Ten graniczny przypadek nazywamy dyfrakcją Fraunhofera. Czoła fal padających jak i ugiętych są płaszczyznami (promienie są równoległe) tak jak to widać na rysunku (b).

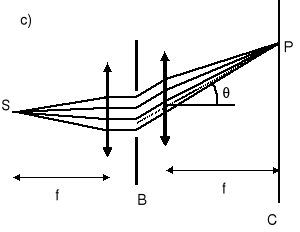
Warunki do wystąpienia dyfrakcji Fraunhofera można zrealizować w laboratorium za pomocą

dwu soczewek (rysunek c).

Pierwsza soczewka zmienia falę rozbieżną w równoległa, a druga skupia w punkcie P fale płaskie opuszczające otwór. Wszystkie promienie oświetlające punkt P opuszczają otwór równolegle do linii przerywanej (przechodzącej przez środek soczewki).

Pojedyncza szczelina

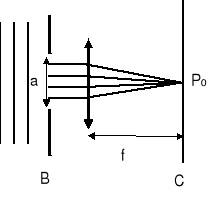
Rysunek pokazuje falę płaską padającą prostopadle na szczelinę o szerokości a. Rozpatrzmy punkt środkowy P₀ ekranu. Równoległe promienie przebywają do tego punktu te same drogi optyczne (różne geometryczne) tzn. promienie zawierają tę samą ilość długości fal (soczewki cienkie). Ponieważ w szczelinie promienie są zgodne w fazie to po przebyciu takich samych dróg optycznych nadal pozostają zgodne w fazie. Dlatego w środkowym punkcie P₀ będzie maksimum.

Interferencja fal, zjawisko wzajemnego nakładania się fal (elektromagnetycznych, mechanicznych, de Broglie itd.). Zgodnie z tzw. zasadą superpozycji fal, amplituda fali wypadkowej w każdym punkcie dana jest wzorem:

gdzie: A₁, A₂ - amplitudy fal cząstkowych, φ - różnica faz obu fal.

Maksymalnie A = A₁+A₂ dla φ=2k (fazy zgodne), minimalnie A=A₁-A₂ dla φ=(2k+1) (fazy przeciwne). Warunkiem zaistnienia stałego w czasie rozkładu przestrzennego amplitudy interferujących fal jest ich spójność (koherentność).

Dla fal mechanicznych i radiowych warunek spójności jest łatwy do uzyskania, natomiast dla światła zazwyczaj wymaga zastosowania układów rozdzielania i kolimowania wiązek (monochromatory) lub stosowania laserów. Wypadkowa fala, powstała z interferencji spójnych fal padających jest falą stojącą, np. dla światła obserwuje się kolejno następujące po sobie jasne i ciemne linie, krzywe, lub okręgi, w zależności od geometrii interferujących fal (tzw. prążki interferencyjne). Ciemne obszary występują w miejscach, gdzie różnica dróg optycznych wynosi δ=(2k+1)λ/2, gdzie: k - dowolna liczba całkowita zwana rzędem interferencji, λ - długość fali. Jasne obszary wystąpią dla δ=(2k)λ/2=kλ.

Interferencja światła

Przy interferencji światła zachodzącej dzięki wielokrotnemu odbiciu w płytce płasko-równoległej otrzymane prążki nazywa się prążkami (interferencyjnymi) równego nachylenia, przy interferencji otrzymywanej dzięki odbiciom w płytce o innych kształtach (klinowatej, sferycznej itp.) otrzymuje się tzw. prążki równej grubości. W przypadku odbicia światła od cienkiej, płaskiej i przezroczystej warstwy naniesionej na inną substancję (np. plamy cieczy hydrofobowej, np. nafty, na wodzie) obserwuje się interferencję światła odbitego od powierzchni nafty ze światłem odbitym od powierzchni granicznej rodzielającej naftę i wodę. W przypadku oświetlenia światłem białym uzyskuje się wygaszenie pewnych, oraz wzmocnienie innych barw, co obserwuje się jako mieniące się, tęczowe plamy barwne na wodzie. Zjawisko nosi nazwę interferencji na cienkich warstwach.

Spójna ( koherentna ) wiązka światła przechodząc przez dwie jednakowe szczeliny ulega na nich ugięciu , dając po przejściu przez szczelinę dwie fale spójne interferujące ze sobą. W wyniku interferencji otrzymuje się na ekranie umieszconym w pewnej odległości za szczelinami jasne i ciemne prążki interferencyjne.

Ćwiczenie , wykorzystuje opisane zjawisko z tą różnicą , że zamiast dwóch znajduje się znacznie więcej jednakowych , równoległych szczelin , których liczba może dochodzić do kilkunastu tysięcy. Tworzą one tak zwaną siatkę dyfrakcyjną.

Fala świetlna po przejściu przez szczeliny interferuje tworząc na ekranie maksima interferencyjne widoczne w postaci prążków ( przede wszystkim I - go rzędu ).

Stałą siatki d ( odległość między środkami każdej pary dwóch sąsiednich szczelin ) obliczamy ze wzorów :

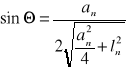
W pierwszej części doświadczenia wyznaczamy stałą siatki dyfrakcyjnej , w drugiej przy znanej już stałej d wyznaczamy długość fal przepuszczanych przez filtr interferencyjny.

Przebieg ćwiczenia

1. Włączamy lampę sodową. Czekamy około pięciu minut, aż będzie świecić mocnym, żółtym światłem.

2. Regulujemy szerokość szczeliny oraz ustawiamy siatkę wraz z soczewką w ten sposób, aby otrzymać na ekranie ostre prążki.

3. Mierzymy odległość a₀ dwu prążków symetrycznych względem prążka zerowego oraz odległość l₀ siatki od ekranu.

4. Znając długośc fali światła lampy sodowej λ₀=5893A oraz odległości a₀ i l₀ obliczamy stałą siatki d.

5. Włączamy wskaźnik laserowy obracając nim o około 90^o. Ustawiamy siatk wraz z soczewką w ten sposób, by otrzymać na ekranie ostre prążki.

6. Mierzymy odległość a_i dwu par prążków oraz odległość l siatki od ekranu. Znając a_i, l oraz stałą siatki obliczamy długość fali dla światła laserowego.

Wnioski i dyskusja błędów.

Wartość błędu zależy w dużej mierze od indywidualnych właściwości oka obserwatora. Jego wartość zwiększa się wielokrotnie w przypadku, gdy obserwator ma wadę wzroku. Duży wpływ na wielkość błędu miał fakt, że błąd pomiaru odległości l jest większy niż dokładność pomiaru odległości prążków a.

Duży wpływ na błąd miała szerokość prążka światła lampy sodowej. Wynosiła ona ok. 1 mm, czyli tyle, ile dokładność przyrządu.

4

---