Nazwisko______________________________
Imię__________________________________
Kierunek______________________________
Rok studiów___________________________
Grupa laboratoryjna_____________________
|
WYŻSZA SZKOŁA PEDAGOGICZNA w Rzeszowie I PRACOWNIA FIZYCZNA |
||||
|
W y k o n a n o |
O d d a n o |
|||
|
Data |
Podpis |
Data |
Podpis |
|
Ćwiczenie nr 67 |
Temat |
||||
CZĘŚĆ TEORETYCZNA
Siatką dyfrakcyjną nazywamy szereg wzajemnie równoległych i leżących w równych odstępach szczelin. Odległość między sąsiednimi szczelinami nazywamy stałą siatki. Zazwyczaj siatkę dyfrakcyjną stanowi szereg rys na szkle, przestrzenie między rysami spełniają rolę szczelin.
Siatki dyfrakcyjne przeznaczone do celów dydaktycznych wykonane są techniką fotograficzną. Światło padające na siatkę doznaje ugięcia na każdej szczelinie i w płaszczyźnie ogniskowej soczewki zbierającej daje maksima podobnie jak w przypadku pojedynczej lub podwójnej szczeliny. Maksima promieni ugiętych są szczególnie wyraźne gdy wzmacniają się promienie wychodzące ze wszystkich szczelin.
Następuje to wtedy gdy między promieniami wychodzącymi z dwóch sąsiednich szczelin różnica dróg wynosi kλ czyli dla kąta αm określonego wzorem;
d⋅sinαm= kλ (1)
różnica dróg skrajnych promieni wynosi wtedy:
N⋅d⋅sinαm= N⋅kλ (2)
gdzie N oznacza liczbę szczelin.
Pierwsze minimum boczne otrzymujemy wtedy, gdy wygaszają się promienie przechodzące od skrajnej szczeliny i środkowej szczeliny, wtedy promienie z kolejnych par liczonych od jednej z krawędzi i od środka zawsze się wygaszają. Odległość tych szczelin wynosi N⋅d /2 a różnica dróg:
N⋅d⋅sinαm / 2 (3)
Warunek na minimum przyjmuje postać:
N⋅d⋅sinαm / 2 = λ / 2 (4)
stąd d⋅sinαm = λ / N (5)
dla i =N , zgodnie z (1) mamy pierwsze maksimum. Zatem pomiędzy kolejnymi maksimami występuje N-1 minimów oraz N-2 maksimów wtórnych, w których natężenie jest bardzo małe.
Wartość sinusa kąta nachylenia αm dla najbliższego minimum sąsiadującego z maksimum określanym wzorem (1) otrzymamy z warunku, że różnica dróg Δ jest sumą różnicy dróg (1) kλ, odpowiadającej maksimum i różnicy dróg (5) λ/N , odpowiadającej najbliższemu minimum. Ponieważ ta różnica dróg Δ=d⋅sinm1 , więc mamy
sinm1 = kλ/d + λ/N⋅d
![]()
dwie linie widmowe λ + δλ i λ możemy rozróżnić wtedy, gdy ich rozsunięcie kątowe (różnica sinusów kątów ugięcia) jest przynajmniej takie, że maksimum linii fali o długości λ + δλ występuje dla tego samego kąta co minimum fali o długości λ.
Wielkość ta nazywa się zdolnością rozdzielczą siatki i jest ona proporcjonalna do całkowitej liczby rys N i do rzędu ugięcia k.
Do wyznaczania długości fali służy prosta aparatura składająca się z ławy optycznej, źródła światła, ekranu ze szczeliną i siatki dyfrakcyjnej. Źródłem jest lampa widmowa lub zwykła lampa z kompletem filtrów optycznych. Na ekranie naniesiona jest podziałka milimetrowa. Przyrząd może być zaopatrzony w układ do zdalnego przesuwania wskazówki, ułatwiający dokładny odczyt położenia linii na podziałce. Dodatkowa luneta służy do zdalnego odczytywania wskazań.
PRZEBIEG ĆWICZENIA
Oświetlamy szczelinę lampą sodową a następnie dobieramy położenie siatki dyfrakcyjnej i soczewki względem ekranu w taki sposób, żeby uzyskać na linii wyraźne prążki widma sodu.
Na podstawie podziałki ekranu odczytujemy odległość dwóch prążków symetrycznych względem prążka zerowego. Mierzymy odległość siatki dyfrakcyjnej od ekranu l0.
Wyznaczamy stałą siatki dyfrakcyjnej a następnie wyznaczamy jej wartość średnią.
TABELA POMIARÓW
DYSKUSJA BŁĘDÓW
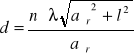
Wyznaczam stałą siatki dyfrakcyjnej z wzoru :
λ= 589,3⋅10-9 m
n= 1
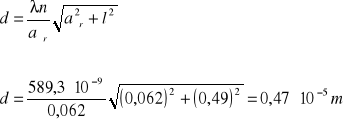
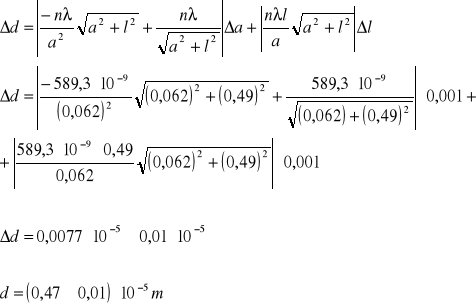
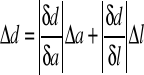
Obliczam błąd d metodą różniczki zupełnej:
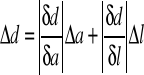
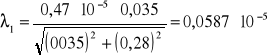
![]()
Obliczam długość fali światła laserowego dla rzędu n=1 ze wzoru:
Obliczam błąd metodą różniczki zupełnej:
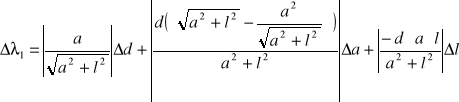
![]()
![]()
![]()
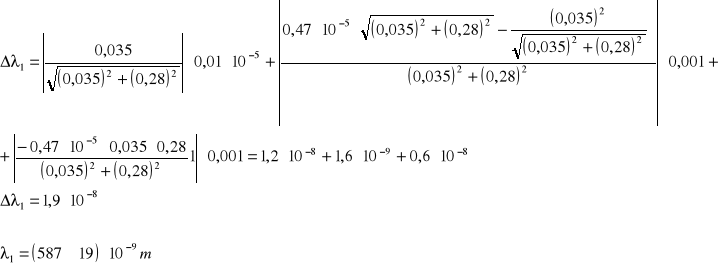
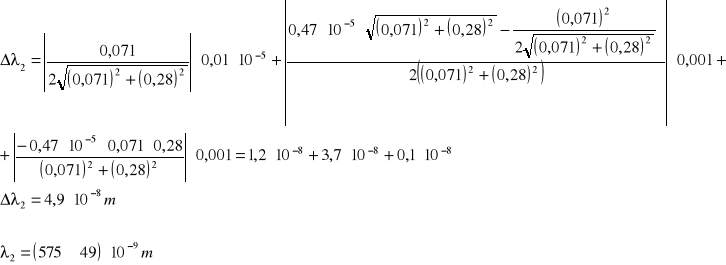
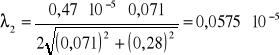
Obliczam długość fali światła laserowego dla rzędu n=2 korzystając ze wcześniejszych wzorów:
Wyniki końcowe:
λ1 = (587±19)⋅10-9 m
λ2 = (575±49)⋅10-9 m
WNIOSKI
Popełnione błędy przy przeprowadzaniu doświadczenia mogły być spowodowane niedoskonałością zmysłów obserwatora oraz ewentualną niedokładnością przyrządów wykorzystywanych w ćwiczeniu. Z porównania wyników widać, że otrzymany przedział długości fal światła laserowego mieści się w przedziale odczytanym na laserze. Zatem można stwierdzić, że doświadczenie zostało przeprowadzone prawidłowo.
![]()
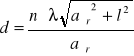
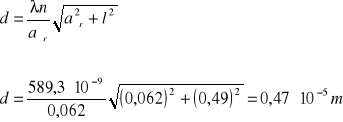
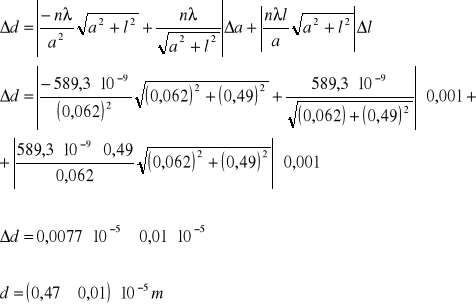
![]()
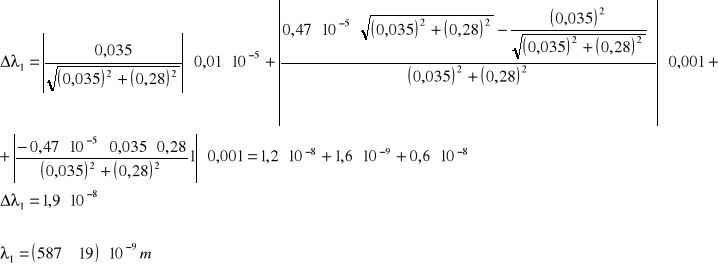
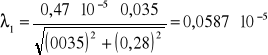
![]()
![]()
![]()
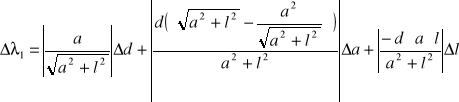
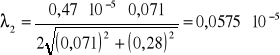
Wyszukiwarka
Podobne podstrony:
Siatka dyfrakcyjna, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćw
67-siatka dyfrakcyjna3, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria
50B, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćwiczenie nr50b
Ćwiczenie nr 35, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćwicz
F-71, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćwiczenie nr71
Kopia 46, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, 46
Lorentza-Lorenza2, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćwi
Badanie widma par rtęci za pomocą spektroskopu, studia, Budownctwo, Semestr II, fizyka, Fizyka labor
92-fotokomórka, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Gotowe
Ćwiczenie nr 44, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćwicz
Ćwiczenie nr 50a, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćwic
Ćwiczenie nr 9, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćwicze
LAWA-2, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćwiczenie nr72
Ćwiczenie nr 33a, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćwi
Pierścienie Newtona1-teoria, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labola
Goniometr - przebieg ćwiczenia, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Lab
Cwiczenie nr 83, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćwicz
więcej podobnych podstron