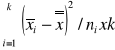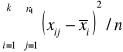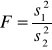Przykład 2

Wysunięto hipotezę, że czas potrzebny na obróbkę pewnego metalowego detalu można zmniejszyć przez zastosowanie innego niż dotychczas typu obrabiarki. Przy niezmienionych innych warunkach, zmierzono dla losowo wybranych sztuk czasy wykonywania tego detalu na dwóch typach obrabiarek i otrzymano dla obrabiarki II (nowej) następujące wyniki (w minutach): 15, 12, 10, 18, 14, 15, 13, a dla obrabiarki I (starej): 17, 11, 22, 18, 19, 13, 14, 16. Zweryfikować wysuniętą hipotezę na poziomie istotności α=0,05.

Rozwiązanie

Mamy do czynienia z modelem II. Stawiamy hipotezę H₀: m₁=m₂, wobec hipotezy alternatywnej H₁: m₁>m₂, gdzie m₁ oznacza średni czas toczenia przy użyciu obrabiarki starej, a m₂ oznacza średni czas toczenia przy użyciu nowo proponowanej obrabiarki.

Z tablicy rozkładu t Studenta należy więc dla α=0,05 oraz dla n₁+n₂-2=13 stopni swobody odczytać taką wartość krytyczną t_α =2.160, by spełniona była nierówność P{t≥t_α}=0,05. Następnie należy wg wzoru (1.7) obliczyć wartość statystyki t. Zauważmy jednak, że

,

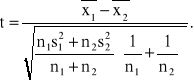
(16 - 14)/sqrt(88-39)/(8+7-2)x(1/8+1/7)

= 2/sqrt2.62 = 1.23

wystarczy zatem obliczyć średnie
i
oraz sumy kwadratów odchyleń od nich.

Otrzymujemy więc wartość statystyki

Ponieważ t_α = 2.160> t =1,23 to nie ma podstaw do odrzucenia hipotezy zerowej. Oznacza to że zakup nowej obrabiarki w celu zwiększenia wydajności pracy jest nieuzasadniony

Zadanie domowe

Niżej zestawiono wyniki dwutygodniowej sprzedaży produktów nabiałowych spółdzielni mleczarskiej „Przyszłość” przed i po zastosowaniu kampanii marketingowej.

Dzień sprzed. Wart sprz. Przed prom Wart. Sprzed po prom

Pon 456 zł 532 zł

Wtor 351 375

Środa 421 495

Czwartek 495 510

Piątek 311 379

Sobota 650 765

Niedziela 234 432

Pon. 486 619

Wtorek 376 438

Środa 478 456

Czwartek 512 543

Piątek 338 456

Sobota 578 650

Niedz 387 398

434,7 503,43

1. Test dla dwóch wskaźników struktury (procentów)

Badając dwie populacje generalne ze względu na cechę niemierzalną musimy często sprawdzać hipotezę, że frakcje elementów wyróżnionych (wskaźniki struktury lub procenty) są w obu populacjach takie same.

Test podany poniżej pozwala na zweryfikowanie tej hipotezy w oparciu o wyniki dwu dużych prób i korzysta się przy tym z asymptotycznego rozkładu normalnego odpowiedniej statystyki. Jak zawsze, w zależności od postaci hipotezy alternatywnej, obszar krytyczny w tym teście buduje się albo dwustronnie, albo też jednostronnie.

Model

Dane są dwie populacje generalne o rozkładach dwupunktowych z parametrami odpowiednio p₁, p₂ (oznaczającymi frakcje elementów wyróżnionych w tych populacjach). Na podstawie dwu dużych prób o liczebnościach odpowiednio n₁ i n₂ (n₁ i n₂ >100) należy sprawdzić hipotezę, że parametry p₁ i p₂ są jednakowe, tzn. H₀: p₁=p₂, wobec hipotezy alternatywnej H₁: p₁
p₂.

Test istotności dla tej hipotezy jest następujący. Z obu prób o liczebnościach n₁ i n₂ wyznaczamy odpowiednie liczby m₁ i m₂ elementów wyróżnionych w tych próbach. Następnie wg wzoru

obliczamy wartość średniego wskaźnika struktury z obu prób
oraz wg wzoru

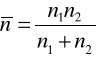
wartość pseudoliczebności próby n. Z kolei obliczamy wartość statystyki

(1.8)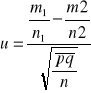
, gdzie

m₁/n₁ i m₂/n₂ są wskaźnikami struktury uzyskanymi z obu prób.

Przykład

W celu sprawdzenia, czy zachorowalność na pylicę jest w pewnym województwie taka sama w mieście jak i na wsi, pobrano z ludności wiejskiej i miejskiej dwie próby, mianowicie z ludności miejskiej wylosowano n₁=1200 osób i otrzymano m₁=40 chorych na pylicę, a z ludności wiejskiej wylosowano n₂=1500 osób i otrzymano m₂=100 osób chorych. Przyjmując poziom istotności α=0,05 należy zweryfikować hipotezę o jednakowym procencie chorych na pylicę w mieście i na wsi w tym województwie.

Rozwiązanie

Zastosujmy powyższy model. Ponieważ nie ma sugestii co to tego, który procent zachorowań na wsi czy w mieście ma być większy, dlatego budujemy dwustronny obszar krytyczny. Formalnie pisząc, stawiamy hipotezę H₀: p₁=p₂, wobec hipotezy alternatywnej H₁: p₁
p₂, gdzie p₁ i p₂ oznaczają nieznane wskaźniki struktury chorych na pylicę odpowiednio w populacji ludności miejskiej i wiejskiej.

Z prób obliczamy

oraz

,

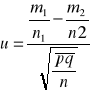
3,4:sqrt0,052x0,948/667

u
-3.9

Z tablicy rozkładu normalnego N(0,1) dla dwustronnego obszaru krytycznego i przy przyjętym poziomie istotności α, odczytujemy krytyczną wartość u_α=1,96. Z porównania wynika, że
, a więc znaleźliśmy się w obszarze krytycznym, zatem hipotezę H₀ odrzucamy. Nie można więc twierdzić, że w tym województwie jednakowa jest zachorowalność na pylicę na wsi i mieście.

2. Test analizy wariancji (klasyfikacja pojedyncza) dla wielu średnich

Omówione testy t-Studenta oraz testy analizy wariancji, należą do grupy tzw. Testów parametrycznych. Oznacza to, że warunkiem stosowania tych testów jest zgodność rozkładu cech z rozkładem normalnym i jednorodność wariancji(wariancje porównywanych szeregów statystycznych nie różnią się istotnie)

Testy analizy wariancji są podstawowym narzędziem statystyki ekspe­rymentalnej w naukach medycznych, rolniczych i technicznych. Testy te pozwalają na sprawdzenie, czy pewne czynniki, które, można dowolnie regulować w toku eksperymentu, wywie­rają wpływ, a jeśli tak, to jak wielki, na kształtowanie się średnich wartości badanych cech mierzalnych. Istotą analizy wariancji jest rozbicie na audytywne składniki (których liczba wynika z potrzeb eksperymentu) sumy kwadratów wariancji całego zbioru wyników. Porównanie poszczególnej wariancji wynikającej z działania danego czynnika oraz tzw. wariancji resztowej, czyli wariancji mierzącej losowy błąd (które to porównanie odbywa się przez zastosowanie testu F Snedecora) daje odpowiedź, czy dany czynnik odgrywa istotną rolę w kształtowaniu się wyników ekspery­mentu.

Testy analizy wariancji mają bardzo liczne zasto­sowania między innymi w analizie regresji.

Model analizy wariancji dla klasyfikacji pojedynczej

Danych jest k populacji o rozkładzie normalnym
(i =1, 2, ... , k) lub o rozkładzie zbliżonym do normalnego. Zakłada się przy tym, że wariancje wszystkich k populacji są równe, tzn.
(lecz nie muszą być znane). Z każdej z tych populacji wylosowano niezależnie próby o liczebności n_i elementów. Wyniki prób oznaczone są przez x_ij (i=1, 2, ..., k, j=1, 2, ..., n_i) przy czym x_ij=m_i+
, gdzie
jest wartością zmiennej losowej nazywanej składnikiem losowym, mają­cej rozkład
. Na podstawie wyników x_ij należy zweryfikować hipotezę H0 : m₁ = m₂ = ... = m_k wobec hipotezy alternatywnej H_l : nie wszystkie średnie badanych populacji są równe.

Test istotności (analizy wariancji) dla tej hipotezy jest następujący. Obliczamy z wyników poszczególnych prób średnie grupowe
i średnią ogólną
.

(1.9)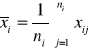
dla i=1,2,...,k

(2.0)
gdzie

Z kolei obliczamy odpowiednie sumy kwadratów i wypełniamy wartościami liczbowymi następującą tablicę analizy wariancji; występująca w niej statystyka F ma przy założeniu prawdziwości hipotezy Ho rozkład F Snedecora o k-1 i n-k stopniach swobody:

Źródło zmienności	Suma kwadratów	Stopnie swobody	Wariancja	Test F
Ogólnej		nxk-1
Między populacjami (grupami)		k-1
Wewnątrz grup (składnik losowy)	Zmienność ogólna - zmienność międzygrupowa	kxn-k

=(
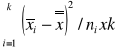
)/ nxk-1
= (
-
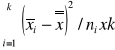
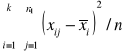
)/ kxn-k

Obliczoną w tablicy analizy wariancji wartość F porównujemy w końcu z wartością krytyczną F_α odczytaną z tablicy rozkładu F Snedecora dla ustalonego z góry poziomu istotności α i dla odpowiedniej liczby k-1 oraz kxn-k stopni swobody. Spełniona ma być przy tym równość P {F
F_α}=α. Jeżeli w wyniku porównania otrzymamy nierówność F
F_α , to hipo­tezę Ho o równości średnich w badanych populacjach należy odrzucić: Natomiast gdy F<F_α , to nie ma podstaw do odrzucenia hipotezy H₀.

Gdy F< 1, to bez porównywania z F_α nie ma podstaw do odrzucenia hipotezy H₀. Odrzucenie hipotezy H₀ oznacza udowodnienie istotnego wpływu podziału na te populacje. W przeciwnym przypadku, wszystkie grupy (populacje) można uznać za równoważne z punktu widzenia otrzymywanych wartości badanej cechy.

Przykład

Koszty materiałowe pewnego wyrobu, który można produkować trzema różnymi metodami, mają rozkład normalny o jednakowej wariancji dla każdej z tych metod. Wylosowane sztuki tego wyrobu dały następujące koszty materiałowe dla poszczególnych metod produkcji (w zł):

Metoda
A	B	C
25 15 20 30 10 - -	40 20 25 50 10 35 -	5 15 20 20 40 10 30

Na poziomie istotności α=0,05 należy zweryfikować hipotezę, że średnie koszty materiałowe są jednakowe dla wszystkich trzech metod produkcji tego wyrobu.

Rozwiązanie

Formalnie biorąc stawiamy hipotezę H₀ : m₁=m₂=m₃, ,gdzie m₁,m₂,m₃ oznaczają średnie koszty materiałowe odpowiednie dla każdej z metod produkcji. Hipotezę tę można zweryfikować za pomocą testu analizy wariancji dla przypadku pojedynczej klasyfikacji. W celu wypełnienia danymi liczbowymi odpowiedniej dla tego testu tablicy analizy wariancji, przeprowadzamy niezbędne obliczenia średnich i sum kwadratów. Z obliczeń tych otrzymujemy

n=n₁+n₂+n₃=18

,
,
,

,
,

,

,
,

Otrzymujemy zatem następującą tablicę analizy wariancji:

Źródło zmienności	Suma kwadratów	Stopnie swobody	Wariancja	Test F
między grupami (metodami)	400,0	2	200,0	F=1,39
Wewnątrz grup (resztkowa)	2150	15	143,3

Z tablicy rozkładu F Snedecora dla przyjętego poziomu istotności α=0,05 i dla liczby stopni swobody 2 i 15 odczytujemy krytyczną wartość F_α=3,68. Ponieważ nie otrzymaliśmy wartości F z obszaru krytycznego, bo F=1,39 < <3;68=F_α, więc nie ma podstaw do odrzucenia sprawdzanej hipotezy Ho o równości średnich kosztów materiałowych przy produkcji tego wyrobu trzema różnymi metodami. Oznacza to, że nie udowodniliśmy, że metody te dają różne średnie koszty materiałowe tego wyrobu. Powodem tego rezultatu jest wysoka wariancja kosztów zużycia materiałów wynikająca przede wszystkim ze zmienności tych kosztów w drugiej technologii.

Przykład marketingowy

Przeprowadzono analizę porównawczą metod promocji

Wartość sprzedaży w tys. zł na dzień dla grupy produktów mleczarskich
	metody promocji
	I	II	III
poniedziałek	3,54	4,43	4,98
wtorek	2,89	3,54	3,55
środa	3,23	3,78	4,5
czwartek	2,75	3,22	4,89
piątek	4,32	4,18	4,67
sobota	4,53	5,03	5,23
niedziela	3,35	4,12	4,65
poniedziałek	3,12	3,98	4,53
wtorek	2,53	3,45	3,87
środa	3,36	3,17	3,67
czwartek	2,65	2,98	3,41
piątek	3,86	3,78	4,08
sobota	4,12	4,57	4,5
niedziela	3,07	4,21	3,99
Suma	47,32	54,44	60,52	Razem
Średnia	3,3800	3,8886	4,3229	162,28
Kwadraty sum	2239,1824	2963,7136	3662,6704	8865,5664
poniedziałek	12,5316	19,6249	24,8004
wtorek	8,3521	12,5316	12,6025
środa	10,4329	14,2884	20,25
czwartek	7,5625	10,3684	23,9121
piątek	18,6624	17,4724	21,8089
sobota	20,5209	25,3009	27,3529
niedziela	11,2225	16,9744	21,6225
poniedziałek	9,7344	15,8404	20,5209
wtorek	6,4009	11,9025	14,9769
środa	11,2896	10,0489	13,4689
czwartek	7,0225	8,8804	11,6281
piątek	14,8996	14,2884	16,6464
sobota	16,9744	20,8849	20,25
niedziela	9,4249	17,7241	15,9201	Razem
Suma	165,0312	216,1306	265,7606	646,9224

Obliczamy sumę kwadratów odchyleń zmienności ogólnej

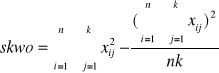
Suma kwadratów odchyleń dla zmienności międzygrupowej

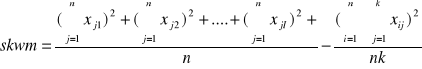
skwm= 633,2547 - 627,019

skwm=6,2357

Suma kwadratów odchyleń zmienności błędu

skwbł=skwo-skwm

skwbł= 19,85-6,2357= 13,61

Źródło zmienności	Suma kwadratów	Stopnie swobody	Wariancja	Test F
Ogólnej	19,85	42-1=41	-
Między populacjami (grupami)	6,2357	3-1=2	6,2357/2=3,1178	8,936**
Wewnątrz grup (składnik losowy)	13,61	3*14-3=39	13,61/39=0,3489

W celu porównania istotności różnic między metodami promocji stosujemy nowy wielokrotny test rozstępu.

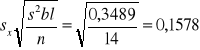
sqrt0,02492

Z tablic wartości krytycznych nowego wielokrotnego testu rozstępu odczytujemy wartości krytyczne dla rozstępu 2 i 3 oraz liczby stopni swobody dla błędu równej 39 wykonujemy następujące obliczenia:

Wyznaczamy przedział ufności

Rozstęp P_0,05 P_0,01 (2) 2,88x0,158 =0,455 3,88x0,158 =0,613

(3) 3,04x0,158 =0,480 4,06x0,158 =0,6415

Rozstęp (2) (3)

Metoda promocji x_śr

III Metoda 4,32

II Metoda 3,89 0,43

I Metoda 3,38 0,51* 0,94**

Analiza istotności różnic pomiędzy średnimi sprzedaży wyrobów uzyskanej po zastosowaniu I, II, i III metody promocji pozwala stwierdzić, że celowe jest zastosowanie III ewentualnie drugiej metody promocji przy rezygnacji ze stosowania metody I.

Zadanie domowe

Przeprowadzono analizę rentowności 4 grup wyrobów przedsiębiorstwa osiąganą w 12 kanałach dystrybucji. Przeprowadzone wcześniej działania restrukturyzacyjne doprowadziły, że wyeliminowano wyroby o deficytowych parametrach efektywności. Asortyment produkcji przedsiębiorstwa stanowiły normalia, w związku z czym wskaźnik rentowności obliczano w zł/100kg wyrobu. W tabeli zestawiono

wskaźniki rentowności w wyodrębnionych grupach asortymentowych uzyskane w roku 2010. Metodą jednoczynnikowej analizy wariancji zweryfikować hipotezę czy rentowność ocenianych grup wyrobów różni się istotnie oraz czy na podstawie przeprowadzonych obliczeń można stwierdzić produkcję których grup należy rozwijać a których ograniczać

Kanały zbytu	Grupa 1	Grupa2	Grupa 3	Grupa4
1.	12,4	8,6	19,3	16,3
2.	10,4	7,5	16,7	15,6
3,	9,6	7,9	15,8	16,2
4.	11,9	8,3	16,4	17,8
5.	12,0	6,5	12,9	13,4
6.	7,3	5,4	8,6	7,6
7.	11,7	9,5	14,3	11,5
8.	8,7	9,8	8,4	9,5
9.	13,2	7,4	15,4	11,5
10,	13,3	10,4	9,8	14,7
11.	8,4	6,8	9,4	12,4
12	7,6	5,7	10,4	8,8

Wartość krytyczna F_{α l,ST sw} dla kolumn 4-1 = 3 oraz dla wierszy 48-4=44 dla 0,05 = 2,83 i dla 0,01 = 4.26

Dla nowego wielokrotnego testu rozstępu

Rozstęp P_0,05 P_0,01

(2) 2,83x sx = 3,81x sx =

(3) 3,01x sx = 4,02x sx =

(4) 3,25x sx = 4,23x sx =

17

---