Przykład 1

Wykonano 10 odczytów wielkości fizycznej X:

I	1	2	3	4	5	6	7	8	9	10
Xi	1690	1697	1685	1705	1674	1686	1678	1693	1681	1701

Należy opracować wyniki pomiarów (zakładając ich normalny rozkład prawdopodobieństwa).

Należy wybrać przedział ufności z prawdopodobieństwem P_u=0.95. Błędów systematycznych nie należy uwzględnić.

Rozwiązanie

Średnia arytmetyczna wartości wyników oddzielnych pomiarów

Estymator odchylenia standardowego wartości średniej

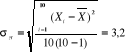
Z tabeli rozkładu Studenta otrzymuje się:

Wynik pomiaru:

X=1689,0;
;P_u=0,95

Przykład 2

Na podstawie świadectwa kalibracji wzorca masa m o wartości nominalnej m_n=1kg wynosi 1000,000323 g z niepewnością całkowitą u_c=
. Określić niepewność standardowa u.

Rozwiązanie:

Niepewność całkowita została określona dla tzw. trzysigmowego przedziału ufności. Odpowiada to jednoznacznie poziomowi ufności α=0,9973, dla którego k(α)=3, wobec tego:

Przykład 3

Określić niepewność standardowa dla miernika przemieszczeń liniowych posiadającego wartość błędu granicznego

Rozwiązanie

Przyjmując założenie, ze błędy przyrządu pomiarowego przyjmują z jednakowym prawdopodobieństwem wartości z przedziału
(maja rozkład jednostajny), otrzymuje się odchylenie standardowe dla rozkładu jednostajnego z zależności

Przykład 4

Przy założonym poziomie ufności p=0.95 należy obliczyć graniczny błąd i niepewność pomiaru wielkości fizycznej X. Miernikiem cyfrowym o niedokładności (granicznym błędzie bezwzględnym)
odczytu + 2 cyfry wykonano serie N=10 pomiarów wartości wielkości fizycznej X otrzymując wyniki w jednostkach [J] zestawione w tablicy:

Tablica. Wyniki pomiarów wielkości X

N	-	1	2	3	4	5	6	7	8	9	10
X(n)	J	0.9028	0.9016	0.9029	0.8956	0.8971	0.8955	0.8991	0.9043	0.9035	0.9025

Pomiary wykonano na zakresie IJ

Rozwiązanie

Średnia arytmetyczna serii pomiarów:

Estymata wariacji pojedynczego pomiaru:

Estymata wariancji średniej arytmetycznej:

graniczny błąd systematyczny (niedokładności) miernika obliczony dla średniej arytmetycznej

graniczny błąd przypadkowy (z rozkładu t-Studenta)

Dla N-1=9, t_0.9s=2.262

graniczny błąd pomiaru jest suma granicznego błędu przypadkowego i granicznego błędu systematycznego:

wynik pomiaru:

X=(0.9005
0.0045)J (na poziomie ufności p=0.95)

Niepewność standardowa pomiaru:

u(x)=1.57mJ

Niepewność rozszerzona pomiaru:

Wynik pomiaru:

X=(0.9005
0,0032)J (ze współczynnikiem rozszerzenia k=2)

Przykład 5

W pomiarze pośrednim należy zmierzyć jednocześnie dwie wielkości fizyczne o wartościach
. Do pomiaru wielkości X śluzy miernik z błędem granicznym względnym
, a do pomiaru wielkości Y służy miernik z błędem granicznym względnym
. Określić błędy graniczne względne pomiaru wielkości Z gdy:

a)
b)
c)
d)

Rozwiązanie

W przypadku mnożenia i dzielenia błąd graniczny względny:

dla dodawania

w przypadku odejmowania

przy obliczaniu błędów granicznych nie uwzględnia się możliwości wzajemnej kompensacji błędów. Otrzymuje się przez to wartości zbyt pesymistyczne.

Przykład 6

Obliczyć moc sygnału podanego na rys 1. zakładając, że całkowita moc sygnału przenoszona jest przez składowe od piątej harmonicznej, wyznaczyć, jaki procent mocy przenosi pierwsza harmoniczna. Trygonometryczny szereg Fouriera dla sygnału ma postać:

Rozwiązanie

Na podstawie twierdzenia Paresevala P=

Z warunków zadania 100% mocy odpowiada

zawartość mocy w pierwszej harmonicznej można określić jako:

Przykład 7

dla sygnału jak na rysunku podać:

1. Współczynnik kształtu

2. Współczynnik szczytu

3. wartość mocy zawartej w składowych powyżej pierwszej harmonicznej.

Trygonometryczny szereg Fouriera dla sygnału ma postać:

a)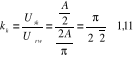
b)

4. Przy założeniu jednostkowej rezystancji (R=1Ω) liczbowo moc składowej stałej i pierwszej harmonicznej wynosi

całkowita moc sygnału jest równa mocy sygnału sinusoidalnego o okresie T=2T₁ i amplitudzie A

moc składowych powyżej pierwszej harmonicznej wynosi

Udział procentowy mocy:

Przykład 8

Zarejestrowano przebieg wielkości mierzonej X(t) jak na rysunku:

Określić częstotliwość graniczna sygnału w oparciu o kryteria:

1. pierwszego miejsca zerowego obwiedni widma

2. spadku amplitudy granicznej harmonicznej poniżej 10% amplitudy pierwszej harmonicznej.

Rozwiązanie

Obliczeni częstotliwości granicznej f_gS1.

szereg wykładniczy Fouriera dla modelu impulsów okresowych o szerokości α ma postać:

dla pierwszego miejsca zerowego obwiedni widma

stad
i

obliczenie częstotliwości granicznej f_gS2

Warunek
zachodzi dla argumentu funkcji

większego od 3π

czyli n>
i f_gS2=

Przykład 9

Jaki powianiem być odstęp równomiernego próbkowania T_p dla sygnału sinusoidalnego o częstotliwości f=1 kHz, aby można było odtworzyć ten sygnał na podstawie próbek z liniowa interpolacja i błędem nie przekraczającym wartości maksymalnej γ_m=1%

Rozwiązanie

Liczbę próbek n przypadających na każdy okres T sygnału sinusoidalnego określa zależność

przykładowo zadanym γ_m odpowiadają wartości n

γ=[%]	0.1	1	10	20
n	70	22	7	5

Dla γ_m=1%

Przykład 10

dla napięcia sinusoidalnego u(t)=sin(ωt+ϕ) z przypadkowa faza początkowa ϕ określić wartość gęstości prawdopodobieństwa p(u) dla u=0

Rozwiązanie

Gęstość prawdopodobieństwa chwilowych wartości napięcia sinusoidalnego z przypadkowa faza początkowa określają zależności:

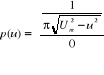
dla u=0 gdzie nachylenie krzywej (stromość napięcia jest największa gęstość p(u) przyjmuje wartość minimalna p(0)=p_min=

Przykład 11

Wyznaczono wartość gęstości prawdopodobieństwa dla wartości średniej szumu N(0,σ_x)

. Należy określić wartość odchylenia standardowego

Rozwiązanie

Gęstość normalna (gaussowska) jest określona wyrażeniem:

dla wartości chwilowych szumu równych wartości średniej

stad

Przykład 12

Ergodyczny proces przypadkowy X(t) posiada funkcje autokorelacji określona wyrażeniem

Należy podać wartość średniokwadratowa, wartość średnia i wariancje dla tego procesu.

Rozwiązanie

Wartość średniokwadratowa procesu

ψ_x=R_x(0)=25+16+36=77

Wartość średnia

X=R_x(
)=36=

Wariancja procesu

D_x=Ψ_x-X²=77-6²=41

Przykład 13

Dla sygnału falowego opisywanego funkcja autokorelacji
. Określić odstęp T_p dla próbkowania sygnału próbkami nieskorelowanymi jeżeli α=100s^-1

Rozwiązanie

Unormowana funkcja autokorelacji wynosi

maksymalny interwał korelacji wynosi τ_MK można obliczyć z warunku

po podstawienie

otrzymuje się
i ostatecznie

Przykład 14

Dana jest funkcja autokorelacji sygnału x(t) w postaci
. Znaleźć odpowiadająca jej gęstość widmowa mocy dwustronna S_x(ϖ) i jednostronna G_s(ϖ)

Rozwiązanie:

Gęstość dwustronna

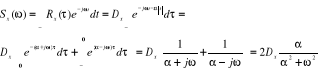
gęstość jednostronna

Przykład 15

Napięcie szumu o normalnej gęstości prawdopodobieństwa p(u) i wartości średniej równej zeru
podano na wejście popularnego multimetru cyfrowego posiadającego w układzie do pomiaru napięcia zmiennego dwu połowkowy prostownik liniowy. Wskazanie przyrządu wyniosło
. Określić wariancje D_u badanego szumu

Rozwiązanie

W popularnych multimetrach wyskalowanych w wartościach skutecznych napięcia sinusoidalnego zależności pomiędzy napięciem wskazywanym U_w a wartością średnia
wynosi:

dla szumu o rozkładzie normalnym słuszna jest zależność:
na podstawie obydwa wyrażeń:

Przykład 16

Dla charakterystyki statycznej y(x)=a₀+a_1x+a₂x² przedstawionej na rysunku obliczyć błąd bezwzględny
dla jej najlepszego przybliżenia liniowego y*(x) dla połowy zakresu zmienności wielkości wejściowej

oraz dla x=0 0 x=x_m

Rozwiązanie

Najlepszym przybliżeniem liniowym dla podanej charakterystyki jest funkcja:

y(x)=a₀-0,125x²_m+(a₁+a₂x_m)x

błąd
jest równy zero dla punktów

dla

dla x=0

dla x=x_m

Przykład 17

Wyniki statycznego wzorcowania przetwornika rezystancja /częstotliwość podane są na rysunku w postaci punktów oraz w tablicy

Rozwiązanie

Szukane parametry znajduje się na podstawie wzorców ogólnych (metoda najmniejszych kwadratów sumy kwadratów):

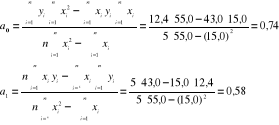
szukana funkcja przetwarzania ma postać

f[kHz]=0,74+0,58R[kΩ]

Przykład 18

Podczas dokonywania pomiaru zależności y=f(x) można wyznaczyć wartości y₁=f(x₁) i y₂=f(x₂), natomiast nie można zmierzyć wartości pośredniej y₀=f(x₀). Należy wyznaczyć przybliżoną wartość y₀ metoda interpolacji dla x₀=1,3 oraz P₁(1;0.3),P₂(1,6;2)

Rozwiązanie

Interpolacje należy przeprowadzić wg zależności, jaka obowiązuje w danym przedziale funkcji y=f(x), najczęściej jednak wybiera się interpolacje liniowa. Wartość y₀ oblicza się z zależności:

Jeżeli poszukuje się wartości x₀ np. dla y₀=0 to

Przykład 19

Przetwornik pokazany na rysunku powinien przenosić sygnały bez zniekształceń (tzn. z zachowaniem kształtu impulsów). Jaka powinna być zależność pomiędzy R₁, R₂, C₁, C₂, aby tego dokonać

Rozwiązanie:

Warunek niezniekształcania sygnału będzie spełniony, jeżeli:
, gdzie k>1. Wynika z tego warunku, ze zmianie w przetworniku niezniekształcajacym może ulec jedynie amplituda.

,

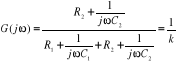
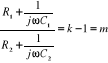
zatem dla

Sygnał wejściowy będzie przenoszony bez zniekształceń. Sygnał będzie tłumiony, układ z rysunku jest wiec dzielnikiem napięcia

Przykład 20

Temperaturę zmienna z okresem T_v mierzona przy wykorzystaniu termopary o stałej czasowej T_c=60s. Obliczyć częstotliwościowy błąd pomiaru γ_f dla wartości okresu T_u z przedziału (0,33.....3) godziny.

Rozwiazanie

Dla przetworników z charakterystyka aperiodyczna błąd γ_f może być obliczony z zależności:

Po podstawieniu odpowiednich wartości częstotliwości otrzymuje się

Tu [godz]	0,33	0,5	1	2	3
-γf [%]	5	2	0,5	0,14	0,06

Przykład 21

Do pomiaru pulsacji ciśnienia użyto tensometrycznego membranowego czujnika z pulsacja ω₀=31,4*10³ rad/s. Przy braku tłumienia (h≅0) obliczyć częstotliwościowy błąd pomiaru dla częstotliwości z przedziału (0....1) kHz.

Błąd częstotliwościowy γ_f określa różnice miedzy rzędnymi charakterystyki amplitudowo częstotliwościowej i stałym poziomem

Rozwiązanie

Błąd
może być obliczony z zależności:

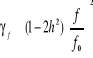
dla h

Przykład 22

Sinusoidalne zmienna temperaturę mierzono termometrem o stałej czasowej T=20s. Częstotliwość zmian temperatury wyniosła f_u=0.02 Hz. Amplituda wskazań termometru δ_mW=12⁰C. Należy obliczyć amplitudę δ_m zmian mierzonej temperatury i opóźnienie τ wskazań temperatury. Czy wybór termometry był właściwy?

Rozwiązanie

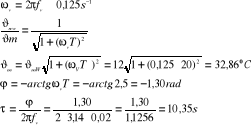
Termometr był wybrany niewłaściwie. Należy zastosować termometr o mniejszej stałej czasowej (ωT<1)

Przykład 23

Dla wyznaczenia odpowiedzi impulsowej przetwornika inercyjnego pierwszego rzędu o charakterystyce amplitudowo - częstotliwościowej jak na rysunku dobrać parametry techniczne realizowanego impulsu Diraca U₁(t)(U_m,α). Określić właściwości częstotliwościowe zaproponowanego sygnału testowego

Rozwiązanie

Dla częstotliwości załamania f_z jest spełniona zależność

2πf_zT=1

Stała czasowa przetwornika

W praktyce dla identyfikacji wystarcza spełnienie warunku

czyli

Można przyjąć wartość α=1s. Amplituda U_m impulsu nie może być większa od granicy, która wyznaczają normalne i dopuszczalne warunki pracy przetwornika. Widmo sygnału testowego o czasie trwania α ma charakter ciągły o częstotliwości granicznej pierwszego zera widma

Przykład 24

Na wejście układu inercyjnego pierwszego rzędu o stałej czasowej T podano szum biały o wartości gęstości widmowej mocy G_x(f)=a. Określić gęstość widmowa mocy G_y(t), wartość średniokwadratowa t_y i funkcje autokorelacji R_y(τ) sygnału wyjściowego układu

Rozwiązanie

Wykorzystać należy zależność ogólna miedzy wejściem a wyjściem układu o transmitancji:

Dla układu iteracyjnego pierwszego rzędu

Wobec tego
dla f>0

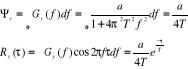
Przykład 25

Wyznaczono charakterystykę amplitudowo - częstotliwościowa przetwornika jak na rysunku. Należy określić rząd przetwornika oraz jego parametry charakteryzujące właściwości dynamiczne

Rozwiązanie

Otrzymana charakterystyka odpowiada modelowi oscylacyjnemu II-ego rzędu (parametry p i ϖ₀) dla małej wartości tłumienia ξ.

Wartość ξ oblicza się z zależności:

Stąd ξ=0,36

Pulsacje ω₀ można obliczyć z wyrażenia:

---