Nieliniowe zagadnienia optymalizacyjne

Program nieliniowy o postaci kanonicznej

Przy rozwiązywaniu programów nieliniowych o postaci kanonicznej znajduje zastosowanie tzw. metoda mnożników Lagrange'a. Tok postępowania można tu podzielić na dwa etapy:

1. Sprawdzamy, czy funkcja celu f(x) ma ekstremum bezwarunkowe. Jeżeli tak, to czy spełnia ono warunki ograniczające, a więc czy jest równocześnie ekstremum warunkowym.

Szukanie ekstremum bezwarunkowego polega na obliczeniu pochodnych cząstkowych funkcji celu względem poszczególnych zmiennych decyzyjnych i przyrównaniu tych pochodnych do zera.

Warunkiem wystarczającym na istnienie minimum funkcji f(x) w punkcie x = (x­_­1, x­_­2, ..., x_n) jest to, aby w tym punkcie wyznacznik macierzy utworzonej z pochodnych cząstkowych drugiego rzędu funkcji był dodatni, tzn.:

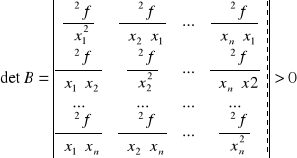
oraz aby wartości wszystkich minorów głównych tej macierzy (brane w punktach stacjonarnych) były dodatnie. Jeżeli ekstremum bezwarunkowe spełnia warunki ograniczające, to zadanie jest już rozwiązane.

2. Jeżeli ekstremum bezwarunkowe nie spełnia ograniczeń, funkcję celu przekształcamy w funkcję Lagrange'a:

przy czym
, to nieoznaczone mnożniki Lagrange'a.

W ten sposób zastępujemy szukanie ekstremum warunkowego funkcji f(x) szukaniem ekstremum bezwarunkowego funkcji Lagrange'a. Obliczamy pochodne cząstkowe funkcji L względem poszczególnych zmiennych decyzyjnych x_j oraz względem mnożników Langrange'a
a następnie przyrównujemy te pochodne do zera. Rozwiązanie otrzymanego układu równań jest na ogół rozwiązaniem optymalnym.

Przykład 1

Z elektrociepłowni energia przesyłana jest do dwóch zużywających ją zakładów produkcyjnych. Funkcja kosztów przesyłania energii do tych zakładów w zależności od wielkości przesyłu (odpowiednio, do zakładu I - x₁ i do zakładu II - x­­₂) dana jest wzorem:

f(x₁,x₂) = 5x₁² - 8x₁x₂ + 7x₂² - 12x₁ - 4x₂ + 81.

Rozdzielić dzienną produkcję energii 16 MWh pomiędzy te dwa zakłady tak, aby zminimalizować koszty przesyłu energii. Podać wysokość tych kosztów.

Rozwiązanie:

Mamy zatem znaleźć minimum funkcji

f(x₁,x₂) = 5x₁² - 8x₁x₂ + 7x₂² - 12x₁ - 4x₂ + 81.

przy warunkach:

g(x₁,x₂) = x₁ + x₂ = 16

1. Sprawdzamy, czy funkcja ma ekstremum bezwarunkowe, obliczając pierwsze pochodne f(x) względem x₁,x₂, i przyrównując je do zera. W wyniku otrzymujemy:

Stąd

x₂ = 68/38 = 34/19 = 1 15/19

oraz

x₁ = 50/19 = 2 12/19

Funkcja f(x) może więc mieć ekstremum bezwarunkowe tylko w punkcie o współrzędnych
.

Macierz drugich pochodnych ma postać:

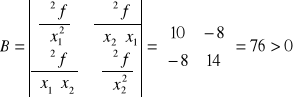
Wyznacznik macierzy jest równy 76 a więc jest większy od 0.

Drugi minor główny tej macierzy 10>0, a więc w punkcie
funkcja f(x) osiąga minimum.

Jednak po podstawieniu współrzędnych otrzymanego punktu do warunku ograniczającego otrzymujemy:

a więc punkt ten nie jest ekstremum warunkowym funkcji f(x) przy warunku g(x₁,x₂).

2. Należy zatem utworzyć dla powyższego zadania funkcję Lagrange'a:

L(x₁,x₂,
) = 5x₁² - 8x₁x₂ + 7x₂² - 12x₁ - 4x₂ + 81 +
(x₁ + x₂ - 16). Obliczamy jej pochodne cząstkowe, które następnie przyrównujemy do zera:

Otrzymujemy układ trzech równań o trzech niewiadomych (x₁,x₂,
), który najłatwiej jest rozwiązać eliminując zmienną
z dwu pierwszych równań. Ostatecznie otrzymujemy:

x₁ = 9, x₂ = 7, f(x₁,x₂) = 189

Zatem zakład I powinien otrzymywać dziennie 9 MWh energii, a zakład II 7 MWh. Koszty przesyłania energii wyniosą 189 jedn. pieniężnych.

Mankamentem omówionej metody jest to, że nie gwarantuje ona uzyskania nieujemnych wartości zmiennych decyzyjnych. Gdyby okazało się, że w otrzymanym rozwiązaniu któraś ze zmiennych przyjęła wartość ujemną, trzeba by uciec się do innych metod rozwiązywania. Stąd też wynika ograniczone zastosowanie metody mnożników Lagrange'a do rozwiązywania programów nieliniowych.

Zadanie 1

Ustal plan produkcji dwóch elektrowni wiedząc, że bieżące dzienne zapotrzebowanie na prąd wynosi 100 MWh tak aby koszty produkcji energii były minimalne. Dzienne koszty zużycia węgla (w tys. zł) używanego do produkcji opisane są następującą funkcją:

f(z₁,z ₂) = 2(z_1­-1)² + (z₂ -3)²

gdzie z₁ oznacza zużycie węgla w elektrowni I, z₂ oznacza zużycie węgla w elektrowni II, Wiadomo ponadto, że z 1 t węgla w elektrowni I uzyskuje się 5 MWh energii, a w elektrowni II - 3 MWh. Podać dzienne minimalne koszty zużycia paliwa w tych elektrowniach. Ile energii powinno być wyprodukowane w elektrowni I a jaki w II? Wartości przedstaw w MWh oraz w procentach.

(11, 15, f 344, 55 MWh, 45 MWh)

Zadanie 2

Dwie cukrownie prowadzą kampanię cukrowniczą mając za zadanie przerobić łącznie
29 760 t buraków. Dzienny przerób pierwszej cukrowni wynosi 120, a drugiej 180 t buraków. Wiadomo, że w trakcie kampanii cukrowniczej powstają straty cukru zależne od czasu składowania buraków, które można opisać następującą funkcją:

f(x₁,x₂) = 0,6 c₁² + 12 c₁ + 0,3 c₂² + 9 c₂

gdzie: c₁ oznacza czas trwania kampanii w cukrowni pierwszej, c_{2 -} czas trwania kampanii w cukrowni drugiej.

1. Jak długo powinna trwać kampania cukrownicza w każdej z cukrowni, aby straty cukru były najniższe? 41; 138; 8455,8

2. W jaki sposób optymalnie rozdzielić owe 29760 t buraków między cukrownie?

4920; 24840

Zadanie 3

Dwie olejarnie o zdolnościach przerobowych 10 t i 15 t ziarna dziennie mają przerobić 1800 t ziarna na olej. Straty oleju w ziarnie zależą od czasie składowania (oczekiwania na przerób), jak również od stosowanych procesów technologicznych uzysku oleju z surowca. Funkcja łącznych strat oleju w ziarnie (w kg) dla obydwu olejarni dana jest wzorem:

f(t₁,t₂) = t₁² + 20t₁ + 3t₂² + 45t₂

gdzie t₁ i t₂ to czasy trwania kampanii odpowiednio w pierwszej i drugiej olejarni. Jak długo powinny trwać kampanie w pierwszej i drugiej olejarni, aby straty oleju w ziarnie były możliwie najmniejsze? Ile ton ziarna powinno być przerobione w poszczególnych olejarniach?

Ekonomia matematyczna II mgr inż. Piotr Betlej

Strona 4/5

---