Zagadnienia na egzamin z analizy II
Przestrzeń
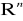
, metryka w przestrzeni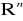
Niech
będzie zbiorem niepustym. Metryką w zbiorze
nazywamy dowolną funkcję
spełniającą następujące warunki:
(i)
;
(ii)
(warunek symetrii);
(iii)
(warunek trójkąta).
Parę
nazywamy przestrzenią metryczną.
Dla dowolnych
liczbę
nazywamy odległością punktów
i
oraz mówimy, że punkty
i
są oddalone od siebie o
Ciągi i granice funkcji w przestrzeni
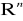
: definicja ciągu w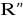
; definicja granicy (właściwej i niewłaściwej) funkcji w punkcie; twierdzenie o zbieżności po współrzędnych; granice iterowane; zależność między istnieniem (nie istnieniem) granic iterowanych a istnieniem (nie istnieniem) granicy podwójnej funkcji w punkcie; twierdzenie o arytmetyce granic
a)Ciągi i granice funkcji w Rn:
Niech
będzie dowolnym zbiorem. Ciągiem o wyrazach w zbiorze
nazywamy dowolną funkcję
Ciąg ten oznaczamy
lub
gdzie
Niech
będzie przestrzenią metryczną,
ciągiem oraz
Mówimy, że
jest granicą ciągu
w metryce
jeśli dla dowolnego
wyrazy ciągu są od pewnego momentu oddalone od
o mnie niż
, czyli
i piszemy
lub
Mówimy, że ciąg
jest zbieżny, jeśli
b) definicja granicy (właściwej i niewłaściwej) funkcji w punkcie
Definicja[Cauchy'ego granicy funkcji w punkcie]
Niech
będzie podzbiorem
Niech
będzie funkcją oraz niech
będzie punktem skupienia zbioru
- Mówimy, że funkcja
ma granicę (właściwą)
w punkcie
jeśli
Piszemy wówczas
- Niech
oraz
punktem skupienia zbioru
Mówimy, że
ma granicę niewłaściwą (w sensie Cauchy'ego)
w punkcie
jeśli
Mówimy, że
ma granicę niewłaściwą (w sensie Cauchy'ego)
w punkcie
jeśli
c) Twierdzenie o zbieżności po współrzędnych
Niech
będzie dowolną przestrzenią metryczną. Niech
będzie ciągiem oraz
Wówczas:
(1)
wtedy i tylko, wtedy, gdy
,
(2) Istnieje co najwyżej jedna granica ciągu
to znaczy
i
(3) Jeśli ciąg
jest zbieżny, to jest ograniczony.
(4) Jeśli
oraz
jest dowolnym podciągiem ciągu
to
(5) Jeśli
jest ciągiem zbieżnym oraz
jest jego dowolnym podciągiem takim, że
to także
(6) Jeśli dla dowolnego podciągu
ciągu
istnieje jego dalszy podciąg
taki, że
to
d) Granice iterowane
b
e) Zależność między istnieniem (nie istnieniem) granic iterowanych a istnieniem (nie istnieniem) granicy podwójnej funkcji w punkcie:
Jeżeli funkcja RxR w R ma granicę w pkt (a,b) i istnieje któraś z granic iterowanych (granica przy x dążącym do a z granicy przy y dążącym do b z f(x,y) lub granica przy y dążącym do b z granicy przy x dążącym do b z f(x,y)) to musi być ona równa granicy funkcji f. w pkt(a,b)
f) Twierdzenie o arytmetyce granic:
Jeśli
jest punktem skupienia zbioru
są funkcjami,
oraz
to
(1)
;
(2)
;
(3)
;
(4)
o ile
oraz dla
mamy
;
(5)
o ile wyrażenia po obu stronach mają sens.
Ciągłość funkcji dwóch zmiennych: definicja funkcji ciągłej w punkcie
, twierdzenie równoważne ciągłości, twierdzenie Weierstrassa o osiąganiu kresów
Ciągłość w przestrzeni metrycznej
Tw. Weierstrassa
Jeśli
jest zbiorem zwartym oraz
jest funkcją ciągłą, to funkcja
osiąga swoje kresy, to znaczy
Pochodne cząstkowe rzędu pierwszego i drugiego: definicja pochodnych cząstkowych rzędu pierwszego i drugiego, tw. Schwarza o pochodnych mieszanych;
a) Mówimy, że funkcja
jest różniczkowalna w punkcie
, jeśli istnieje granica ilorazu różnicowego
Granicę tę - jeśli istnieje - nazywamy pochodną funkcji
w punkcie
i oznaczamy symbolem:
lub
. Funkcję
, która argumentowi
przyporządkowuje wartość pochodnej
funkcji
w punkcie
nazywamyfunkcją pochodną funkcji
lub - krótko - pochodną funkcji
. Zwróćmy uwagę, że dziedzina pochodnej
jest zawsze podzbiorem dziedziny funkcji
.
b) Niech
będzie funkcją różniczkowalną w przedziale otwartym
. Rozważmy funkcję pochodną
Definicja 10.1.
Jeśli funkcja
jest różniczkowalna w punkcie
, to znaczy, jeśli istnieje granica ilorazu różnicowego:
to mówimy, że funkcja
jest dwukrotnie różniczkowalna w punkcie
, a granicę tę nazywamy pochodną rzędu drugiego (lub krótko: drugą pochodną) funkcji
w punkcie
i oznaczamy symbolem
lub
albo
, bądź też
.
c) Tw. Schwarza
Twierdzenie Schwarza lub twierdzenie Clairaut że jeśli dla funkcji
drugie pochodne mieszane istnieją i są ciągłe na zbiorze
, to:
gdzie
Różniczkowalność funkcji: definicja różniczkowalności funkcji w punkcie (x0,y0), warunek konieczny i dostateczny różniczkowalności; zależność między pochodnymi cząstkowymi a różniczkowalnością funkcji; twierdzenie o pochodnej funkcji złożonej; twierdzenie o pochodnych cząstkowych funkcji złożonej.
Definicja różniczkowalności funkcji.
Mówimy, że funkcja ![]()
jest różniczkowalna (różniczkowalna lewostronnie, prawostronnie) w punkcie ![]()
jeśli ma w tym punkcie skończoną pochodną (pochodną lewostronną, prawostronną).
Mówimy, że funkcja ![]()
jest różniczkowalna w przedziale otwartym, jeśli jest różniczkowalna w każdym punkcie tego przedziału.
Mówimy, że funkcja ![]()
jest różniczkowalna w przedziale domkniętym, jeśli jest różniczkowalna w każdym punkcie wewnętrznym tego przedziału, oraz prawostronnie różniczkowalna w lewym krańcu i lewostronnie różniczkowalna w prawym krańcu.
Ekstrema funkcji dwóch zmiennych: definicja, warunek konieczny istnienia ekstremum, warunek dostateczny istnienia ekstremum
a) Twierdzenie Fermata (warunek konieczny istnienia ekstremum)
Jeżeli funkcja f ma ekstremum lokalne w punkcie ![]()
oraz jest różniczkowalna w tym punkcie, to ![]()
.
Pochodna kierunkowa funkcji, gradient funkcji, pochodna kierunkowa a gradient funkcji
Funkcje uwikłane: definicja, twierdzenie o istnieniu i różniczkowalności funkcji uwikłanej, twierdzenie o ekstremach funkcji uwikłanej
Całki podwójne: definicja całki podwójnej po prostokącie, tw. o całkowalności funkcji ciągłych, liniowość całki, addytywność całki względem obszaru całkowania, tw. o zamianie całki podwójnej na iterowane, całka z funkcji o rozdzielonych zmiennych; definicja obszarów normalnych względem osi układu, całki iterowane po obszarach normalnych, obszar regularny, całka po obszarze regularnym, o całkowaniu funkcji nieciągłych; definicja współrzędnych biegunowych, zależność między współrzędnymi biegunowymi (walcowymi, sferycznymi) a kartezjańskimi; Jacobian przekształcenia; zastosowania całek podwójnych
Całki krzywoliniowe: łuk zwykły, łuk skierowany, krzywa zorientowana dodatnio (ujemnie),punkt osobliwy, krzywa gładka, krzywa regularna, całka krzywoliniowa nieskierowana (skierowana), twierdzenie o zamianie całki krzywoliniowej nieskierowanej (skierowanej) na całkę oznaczoną, obszar jednospójny, krzywa Jordana, twierdzenie Greena, twierdzenie o niezależności całki krzywoliniowej od kształtu drogi całkowania; definicja różniczki zupełnej
Miłej nauki
Wyszukiwarka
Podobne podstrony:
Opracowanie Zagadnień na egzamin Mikroprocki
Opracowanie zagadnień na egzamin z MO
Przemiany geopolityczne (opracowane zagadnienia na egzamin)
Opracowane zagadnienia na egzamin
Andragogika opracowane zagadnienia na egzamin
opracowane zagadnienia na egzamin, ►► UMK TORUŃ - wydziały w Toruniu, ►► Socjologia, Praca socjalna,
Dydaktyka [opracowane zagadnienia na egzamin], Metodyka nauczania, język polski, teksty i notatki, e
Opracowanie zagadnień na egzamin z judaizmu, 2. GENEZA JUDAIZMU, Religia patriarchów
Konflikty opracowanie zagadnien na egzamin 2
opracowane zagadnienia na egzamin piachy
Opracowanie Zagadnień na egzamin Mikroprocki ściąga
Nauka?ministracji Opracowanie zagadnień na egzamin z NA
Zestaw 1, Opracowane zagadnienia na egzamin
Zestaw 15, Opracowane zagadnienia na egzamin
ściąga opracowane zagadnienia na egzamin piachy
Zestaw 22, Opracowane zagadnienia na egzamin
Zagadnienia na egzamin z OSR, Studia Finanse i Rachunkowość UMCS, III rok, Oranizacja Systemu Rachun
Zamowienia publiczne - zagadnienia na egzamin, Materiały - studia, I stopień, Zamówienia publiczne
więcej podobnych podstron