Logika 1-8

1. Rozdział Ogólne wiadomości o języku jako systemie znaków

1. Pojęcie znaku

1. Znak- dostrzegalny układ rzeczy czy zjawisko spowodowane przez kogoś, które poprzez zwyczajowo ukształtowane reguły wiąże z owym znakiem lub zjawiskiem konkretne myśli

2. Oznaka - to co współtowarzyszy rożnym zjawiskom czy zdarzeniom

2. Znaki słowne. Język

1. Język - system obejmujący wyznaczony przez pewne reguły zbiór znaków słownych z którymi odpowiednie reguły każą wiązać odpowiednie myśli ( z semiotycznego pkt. widzenia: zasób słów danego języka, reguły znaczeniowe, reguły składniowe-syntaktyczne)

2. Język sztuczny - ustalony odgórnie skonstruowany do jakichś specyficznych celów (np.: esperanto)

3. Język naturalny - taki którego reguły zostały ustalone obyczajowo na przełomie wielu lat w sposób spontaniczny

4. Homonim - wyraz posiadający wiele znaczeń

5. Słownictwo - zasób słów mających ustalone znaczenie w danym języku

6. Słownik czynny - wyrazy którymi posługujemy się na co dzień

7. Słownik bierny - zasób słów rozumianych , choć nie używanych

8. Idiom - wyrażenie złożone mające swoje odrębne znaczenie

3. Kategorie syntaktyczne

1. Funktory - wyrażenia bądź wyrazy nie będące zdaniami ani nazwami , służa do wiązania jakichś wyrażeń w wyrażenia bardziej złożone

1. zdaniotwórcze - w wyniku których powiązanie daje zdanie

2. nazwotwórcze - w wyniku których powiązanie daje nazwę

2. argumenty - wyrazy, wyrażenia łączone za pomocą fuktorów (wyróżniamy funktory o argumentach nazwowych i zdaniowych)

4. Role semiotyczne wypowiedzi

1. Role

1. opisowa (znaczenie czy tak jest czy nie)

2. ekspresywna (uczuciowa)

3. sugestywna ( przed Saint pragmatyki

4. performatywna ( akty o charakterze umownym )

2. nieporozumienie - wywołanie u odbiorcy poprzez ustalone znaki lub słowa toku myślowego którego NIE chciał przekazać nadawca

3. niezrozumienie - NIE wywołanie u odbiorcy poprzez ustalone znaki lub słowa toku myślowego który chciał przekazać nadawca

4. porozumienie - wywołanie u odbiorcy poprzez ustalone znaki lub słowa toku myślowego który chciał przekazać nadawca

2. Rozdział Nazwy

1. Pojęcie nazwy

1. Nazwa - wyraz ub wyrażenie nadane podmiotowi lub orzecznikowi orzeczenia ustalone jednoznacznie rozumienie

1. prosta - składające się z jednego wyrazu

2. złożone - składające się z wielu wyrazów

2. Nazwy konkretna a nazwy abstrakcyjne

1. Nazwy konkretne - odnoszące się do przedmiotu lub osoby ewentualnie czegoś co sobie wyobrażamy jako rzecz lub osoba

2. Nazwy abstrakcyjne - które nie są znakami rzeczy osób ani czegoś, co jesteśmy w stanie wyobrazić sobie. Wskazują na pewna cechę wspólna(białość) albo pewien stosunek pomiędzy przedmiotami (wyższość) lub zdarzenie albo stan rzeczy( kradzież)

3. Błąd hipostazowania - doszukiwanie się przedmiotu fizycznego opisanego przez nazwę abstrakcyjną

3. Desygnat nazwy

1. Desygnat nazwy - przedmiot którego dana nazwa jest znacznikiem

4. Nazwy indywidualne a nazwy generalne

1. Nazwy indywidualne - opisujące dany specyficzny przedmiot nadający cechy wyróżniające (Poznań, Karol Kaczmarek)

2. Nazwy generalne - przysługujące przedmiotom ze względu na cechy które tym przedmiotom przypisujemy(np. budynek, ławka)

3. Przykład : najsłynniejsze z pierników miasto w Polsce ( generalna) = Toruń (indywidualna)

5. Treść nazwy

1. Treść nazwy generalnej - zespół cech na podstawie których osoba używająca danej nazwy we właściwy dla danego języka sposób gotowa jest uznać jaiś dowolny przedmiot za desygnat tej nazwy jeślii stwierdzi w nim cechy łączne

2. Konstytutywny zespół cech - zespół danych cech które pozwalają odróżnić desygnaty danej nazwy od innych przedmiotów

3. Cechy konstytutywne(istotne) - cechy tworzące zespół cech konstytutywnych

4. Cechy konsekutywne - pozostałe cechy wspólne desygnatów danej nazwy

5. Treść leksykalna - konstytutywny zespół cech który jest najprostszy do zrozumienia

6. Supozycje - różne role znaczeniowe

1. prosta - nazwa może być używana w wypowiedzi jako znak dla poszczególnego przedmiotu

2. formalna - wyraz może być nazwą dla całego gatunku przedmiotów

3. materialna - użycie wyrazu jako znaku dla niego samego ( Np. dla wyrazu „zając” będzie to wyraz „zając”)

6. Zakres nazwy, klasa

1. Klasa - mnogość elementów wyróżniona według konkretnych zasad

2. Klasa elementów - charakteryzowana jest przez cechy na podstawie których zalicza się do niej poszczególne elementy

3. Zakres nazwy - to klasa wszystkich desygnatów danej nazwy

4. Nazwa ogólna - mające wiecej niż jeden desygnat

5. Nazwa jednostkowa - mające jeden desygnat

6. Nazwy puste - nie mające desygnatów

7. Nazwy zbiorowe, agregat

1. Agregat - określenie jakiejś całości rzeczy złożonej z części składowych

2. Nazwy zbiorowe - nazwy których desygnatami są NIE poszczególne rzeczy lecz takie przedmioty które traktujemy jako agregaty złożone z poszczególnych rzeczy

8. Nazwy a funktory nazwowe

1. Nazwy według:

1. liczby wyrazów składowych

1. proste

2. złożone

2. charakteru tego do czego się odnoszą

1. konkretne

2. abstrakcyjne

3. sposobu wskazywania desygnatów

1. generalne

2. indywidualne

4. liczby desygnatów

1. ogólne

2. jednostkowe

3. puste

5. struktury desygnatów

1. zbiorowe

2. niezbiorowe

9. Ostrość zakresu nazwy

1. Nazwa ostra - (ostry zakres) jeśli jesteśmy w stanie stwierdzić czy dany przedmiot z którym się dobrze zapoznaliśmy, jest desygnatem pewnej określonej nazwy

2. Nazwa nieostra - jeżeli pomimo dobrego zapoznania się z przedmiotem i jego cechami nie jesteśmy w stanie stwierdzić czy jest czy nie jest ondesygnatem danej nazwy

3. Nazwy wyraźne - umiemy podać zespół ich cech wystarczających do odróżnienia desygnatów

4. Nazwy intuicyjne - na podstawie ogonego wygladu przedmiotu bez zastanawiania się nad teścia danej nazwy umiemy określić czy jest on czy nie desygnatem tej nazwy

3. Rozdział Stosunki między zakresami nazw

1. Wyjaśnienia wstępne

1. Klasa uniwersalna (przedmiotów) - to klasa obejmująca wszelkie przedmioty ( w szerokim znaczeniu tego slowa) w świecie

2. Klasa negatywna - uzupełniająca klasę wydzieloną przez dany desygnat do klasy uniwersalnej

2. Rodzaje stosunków między zakresami nazw (s,p)

1. Zamienności - istnieją przedmioty które SA jednocześnie desygnatami nazy s oraz p lecz nie ma takich desygnatów nazwy s które nie były by desygnatami nazwy p i na odwrót (np.: s= jedno z czterech najludniejszych miast nad Wisłą, P= miasto nad Wisłą posadające uniwersytet (Kraków, Warszawa, Toruń, Gdańsk))

2. Podrzędności ( zakresu nazwy s względem p) - istnieją przedmioty, które SA desygnatami i nazwy s i nazwy p nie ma takich przedmiotów które byłyby s nie będąc zarazem p ale są takie które SA desygnatami p choć nie są s (np.: s= wróbel p=ptak)

3. Nadrzędności (zakresu s względem p ) - istnieją przedmioty, które są desygnatami nazwy s i nazwy p, prócz tego są przedmioty będące desygnatami nazwy s, które nie są desygnatami nazwy p, lecz nie ma takich, które byłyby desygnatami p nie będąc desygnatami s (np: s= lekarz p = chirurg)

4. Krzyżowania - istnieją s, które są zarazem p istnieją s, które nie są p, oraz istnieją p, które nie są s. (Np. s = student p = inwalida)

5. Wykluczania - istnieją s, które nie są p, istnieje p które nie są s, natomiast nie istnieją takie przedmioty które były by desygnatami nazwy s i zarazem nazwy p (np.: s= nos p= pięść)

1. sprzeczność np. sędzia i nie-sędzia

2. przeciwieństwo - dwie nazwy nie mają wspólnych desygnatów, lecz suma tych dwóch nazw nie daje uniwersalnej klasy (np. osioł słowik)

4. Rozdział Definicje

1. Definicje realna a nominalna

1. Definicja realna - jest to zdanie (wypowiedz w jezyku pierwszego stopnia) podające taką charakterystykę pewnego przedmiotu czy tez przedmiotów jakiegoś rodzaju, którą tym i tylko tym przedmiotom można przypisać. Przy czym żąda się by ta charakterystyka „ujmowała istotę” tych przedmiotów, to jest by była tak dobrana, aby można było na jej podstawie wywnioskować o możliwie wszystkich uznawanych za ważne cechach tych przedmiotów.

2. Definicja nominalna - to wyrażenie w ten czy inny sposób podające informacje o znaczeni jakiegoś słowa czy słów (słów definiowanych). Definicja nominalna podaje informacje o znaczeniu definiowalnego słowa, jest tedy wypowiedzią w języku drugiego stopnia, a więc czymś zupełnie innym rodzajowo niż formułowana w języku pierwszego stopnia definicja realna.

2. Rodzaje definicji ze względu na ich zadania

1. Sprawozdawcza - wskazuje jakie znaczenie ma czy też miał kiedyś definiowany wyraz w pewnym języku. Definicja taka składa sprawozdanie z tego , jak pewna grupa ludzi posługuje się lub posługiwała się pewnym wyrazem czy wyrażeniem.

2. Projektująca - ustala znaczenie pewnego słowa na przyszłość, w projektowanym sposobie mówienia. Mianowicie przez definicje projektującą ustanawia się regułę znaczeniową co do tego jakie danemu słowu czy wyrażeniu ma być w przyszłości nadane znaczenie.

1. Konstrukcyjna - ustala znaczenie wyrazu na przyszłość nie licząc się z jego obecnym znaczeniem ( nie podlega falsyfikacji)

2. Regulująca - ustala znaczenie wyrazu na przyszłość licząc się z jednak z jego dotychczasowym (niedostatecznie określonym) znaczeniem ( może z nazwy nieostrej zrobić ostra)

3. Rodzaje definicji ze względu na ich budowę

1. Równościowa - składa się z 3 części:

1. dafinideum - zwrot językowy zawierający wyraz definiowany

2. zwrot , który stwierdza ze dafinideum ma takie samo znaczenie jak wyrazy zawarte w trzeciej części definicji

3. definiens - zwroty i wyrażenia tłumaczące definiowany wyraz

2. Równościowa klasyczna:

1. stylizacja słownikowa - (wyrażenie A jest naszym zdaniem wyrażeniem B mające cechę C) - pewien wyraz czy wyrażenie ma takie samo znaczenie jak wskazywane drugie wyrażenie

2. stylizacja semantyczna - (wyrażenie A oznacz przedmioty B mające cechę C) - pewien wyraz czy wyrażenie oznacza takie a takie przedmioty lub odnosi się do takich a takich cech zdarzeń czy stosunków

3. stylizacja przedmiotowa - ( przedmioty z gatunku A - to przedmioty rodzaju B wyróżniające się cechą C) wskazuje znaczenie wyrazu definiowanego mówiąc o cechach tego , do czego wyraz definiowany się odnosi, albo wymieniając gatunki przedmiotów, które obejmuje dany rodzaj

3. Definicje przez postulaty (aksjomaty) - definiowany wyraz umieszczamy w zdaniu lub kilku zdaniach, których inne wyrazy maja znajome znaczenie i na podstawie przykładu posługiwania się wyrazem definiowanym w tych daniach pozwalamy się innym domyślać, jakie znaczenie nadajemy danemu wyrazowi. Jeśli postulaty nie określają wyczerpująco sposobu posługiwania się definiowanym wyrazem definicje nazywamy cząstkową

4. Warunki poprawności definicji

1. Błędy

1. ignotum per ignotum (nieznane przez nieznane) - tłumaczenie nieznanego wyrazu bądź wyrażenia przez inne również nieznane

2. idem per idem ( to samo przez to samo) - wyraz definiowany znajduje się w części definiens Np.; Logika jest nauką o myśleniu zgodnym z zasadami logiki (błędne kolo bezpośrednie)

3. błędne koło pośrednie - wyraz A definiujemy przez wyrażenie B które definiujemy przez wyr. C a te z kolei musily definiowac za pomocą wyrażenia A

4. definicja za szeroka - zakres definiens obejmuje jakieś przedmioty nie należące do zakresu definiendum (np. prokurator to pracownik prokuratury)

5. definicja za wąska - zakres definiens nie obejmuje wszystkich przedmiotów należących do definiendum (np. zwykły ołówek to przyrząd do pisania złożony z pręcika grafitowego umieszczonego w niebieskiej oprawce z cedrowego drewna)

6. błąd przesunięcia kategorialnego - gdy zakresy definiens i definiendum się wykluczają

5. Rozdział Podział logiczny

1. Pojęcie podziału logicznego

1. Przeprowadzić podział logiczny zakresu jakijś nazwy N na zakresy nazw A, B, C, D…, to znaczy stwierdzić, iż każdy desygnat nazwy N jest desygnatem jednej i tylko jednej z nazw A, B, C, D…, Trzeba wiec przeprowadzając podział logiczny zakresu pewnej nazwy, wskazać dwie lub więcej nazw, których zakresy są podrzędne względem zakresu dzielonego, czyli wskazać mniejsze klasy w obrębie poddanego podziałowi zakresu nazwy.

2. Całość dzielona - zakres który zostaje poddany podziałowi

3. Człony podziału - wyróżniające się w podziale zakresy nazw podrzędnych

2. Warunki poprawności podzialu logicznego

1. Wyczerpujący - jeśli każdy z desygnatów nazwy, której zakres dzielimy, może być zaliczony do jakiegoś wyróżnionego członu podziału

2. Rozłączny - jeśli żaden z desygnatów nazwy, której zakres dzielimy nie może być zaliczony do dwóch członów podziału na raz.

3. Zasada podziału ( fundamentium divisionis)- wyróżnisz człony podziału według jakiegoś jednego sposobu

4. Podział dychotomiczny - dokonany według cech kontradyktorycznych (sprzecznych)

5. Podział według determinanty - podział ze względu na posiadane cechy np.: ołówki podzielić możemy ze względu na kolor „oprawki” lub twardości grafitu

3. Klasyfikacja

1. Klasyfikacja - wielostopniowy podziałlogiczny, podział logiczny z dalszym podzialem członów podziału.

4. Wyróżnianie typów a podział logiczny

1. Wyróżnianie typów przedmiotów - w jakim stopniu przedmioty z pewnego zbioru mają cechy zbliżone do przedmiotu o interesujących nas cechach

2. Przedmiot typowy - przedmioty które mają odpowiednio mało różnią się od przedmiotu z którym je porównujemy

3. Partycja - czynność myślowa polegająca na dzielniu wyróżnianiu składowych części danego przedmiotu np.: roślina dzieli się na korzeń, łodygę, liście i kwiat

6. Rozdział Zdanie

1. Pojęcie zdania w sensie logicznym

1. Zdanie - wyrażenie jednoznacznie stwierdzające, na gruncie reguł danego języka iż tak jest lub tak nie jest., może być prawd lub fałszem.

2. Zdarzenie - fakt że rzecz czy osoba R w momencie T wykazywała własność W, a w innym momencie T1 tej własności nie wykazywała( albo odwrotnie)

3. Stan rzeczy to fakt, iż rzeczy czy osoba R w okresie T do momentu T1 nieprzerwanie wykazywała własnośc W

2. Wartość logiczna zdania

1. Zdanie prawdziwe - opisujące rzeczywistośc taką jaka jest

2. Zdanie fałszywe - opisujące rzeczywistość niezgodnie z tymjak się ona ma

3. Wartość logiczna zdania - prawdziwośc lub fałszywość zdania

3. Obiektywny charakter prawdziwości i fałszywości zdań

1. Zdanie analityczne - takie któremu nie można zaprzeczyć ze względu na sens użytych w nim wypowiedzi np. minuta ma 60 sekund

2. Zdanie wewnętrznie kontradyktoryczne - fałszywe ze względu na sens użytych w nim wyrażeń np.: sześcian jest linią

3. Zdania syntetyczne - takie których wartości logicznej nie jesteśmy w stanie poznać w świetle reguł wyznaczających znaczenie użytych w nim słów, w tym przypadku szukamy probierza prawdziwości (odpowiednika rzeczywistości)

4. Wypowiedzi niezupełne

1. Wypowiedz zdaniowa niezupełna - takie wyrażenie, które na gruncie danego języka nie jest zdaniem w sensie logicznym, lecz o tyle spełnia rolę zdania w sensie logicznym, o ile słuchacz zdaje siebie sprawę z pewnych domyślnych uzupełnień wypowiedzi, pominiętych przez mówiącego

5. Funkcje zdaniowe

1. Funkcja zdaniowa (formuła zdaniowa) - takie wyrażenie opisowe, które zawiera zmienne (x, y, z, S, M, itd.) Wyrażenie takie po dokonaniu odpowiednich podstawień na miejsce zmiennych staje się zdaniem w sensie logicznym. (np. każde S jest P funcja zdaniowa ze zmiennymi nazwowymi, jeżeli p to q funkcja zdaniowa ze zmiennymi zdaniowymi)

2. Kwantyfikator ogólny - znak używany do oznaczenia funkcji zdaniowej która po podstawieniu dowolnych zmienych nazwowych będzie zawsze dawała taki sam wynik zdania logicznego

3. Kwantyfikator szczegółowy ( istnieje ) - znak oznaczających iż przy niektórych podstawieniach pod zmienne zdanie jest prawdziwe lub fałszywe

6. Struktura zdania

1. Zdanie proste - zdanie którego żadna cześć nie jes odrębnym zdaniem

2. Zdanie złożone - zdanie w obrębie którego występuje część będąca innym zdaniem

3. Zdania egzystencjalne - orzekające o istnieniu bądź nieistnieniu danego zjawiska ( jest istnieje a = ex a)

4. Zdania atoniczne - orzekające ze jakieś indywiduum x, określona jednostka oznaczona nazwą indywidualna przynależy lub nie do określonej klasy A co zapisujemy
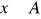
   podmiotemjest jakaś nazwa indywidualna x a orzeczeniem jakaś nazwa generalna

5. Zdania subsumcyjne - orzekające ze jakaś klasa A w całości czy w części zawiera się (nie zawiera się ) w jakiejś klasie B

6. Rodzaje zdań:

1. ogólno twierdzące o budowie „każde S jest P „( funkcja S a P)

2. ogólno-przeczące o budowie „Żadne S nie jest P”(funkcja SeP)

3. szczegółowo-twierdzące o budowie „Niektóre S są P” (funkcja S i P)

4. szczegółowo-przeczące o budowie „Niektóre S nie są P” (funkcja S o P )

7. Odpowiedniki zdania w naszej świadomości

7. Rozdział Funktory prawdziwościowe a spójniki międzyzdaniowe mowy potocznej

1. Pojęcie funktora prawdziwościowego

1. Funktor prawdziwościowy - są to takie funktory zdaniotwórcze o argumentach zdaniowych, których znaczenie określane jest przez to iż przy danej wartości logicznej argumentów zdaniowych takiego funktora jednoznacznie określana jest wartość logiczna całego zdania zbudowango z tego funktora i z tych argumentów.

2. Matryca funktora prawdziwościowego - zestawienie zależności między wartością logiczną dowolnego zdania p oraz wartościa logiczną zdania złożonego z funktora negacji zdania p

3. Funktor koniunkcji - (ozn ^ lub & lub * lub Kpq)
   

4. Funktor alternatywy nierozłącznej
   

5. Funktor alternatywy rozłącznej
   

6. Funktor dysjunkcji
   

7. Funktor równoważności
   

8. Funktor implikacji
   (p - poprzednik implikacji q- następnik)

2. Negacja

1. Para zdań względem siebie sprzecznych - zdanie q i zdanie nie q ( ~q)

2. Zasada sprzeczności (T1) - zdania sprzecznie wzajemnie nie mogą być oba prawdziwe (~(
   ))

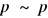
3. Zasada wyłączonego środka(T2) - zdania sprzeczne wzajemnie, nie mogą być oba fałszywe ( pv~p)

4. Zasada podwójnego przeczenia(T3) - negacja negacji ma tą samą wartość co podwójne zanegowanie (
   )

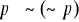
3. Koniunkcja

1. W znaczeniu koniunkcyjnym mówi się ze A jest B i C .. czyli A jest B i A jest C

2. W znaczeniu enumeracyjnym mówi się ze A i B są C tzn A należy do C i B należy do C

3. W znaczeniu syntezującym A i B razem wzięte to C

4. Alternatywa nierozłączna, alternatywa rozłączna, dyzjunkcja

1. „lub” alternatywa nierozłączna

2. „albo” alternatywa rozłączna

3. „bądź” dyzjunksja

5. Równoważność

1. Równoważnośc nie znaczy równożnaczność

6. Implikacja i stosunek wynikania

1. Przyczynowy - stwierdzenie ze coś jest czegoś przyczyną

2. Strukturalny - powstały z takiego a nie innego rozmieszczeniaprzedmiotów w przestrzeni

3. Tetyczny - powstały z czyjegoś ustanowienia

4. Analityczny - związany z samym sensem użytych słów

5. Logiczny - wyniknie jakiegoś zdania z innego

6. Jeżeli z poprzednika implikacji wynika jej następnik to poprzednik nazywa się RACJĄ, a następnik następstwem ( implikacja jest już wtedy prawdziwa)

8. Rozdział Podstawowe pojęcie dotyczące relacji

1. Zadania stwierdzające relacje

1. xRy ( x pozostaje w stosunku R do y )

2. x - poprzednik stosunku (relacji)

3. y - następnik stosunku (relacji)

4. dziedzina stosunku - poprzedniki danego stosunku

5. przeciw dziedzina - przedmioty które są następnikami

6. 
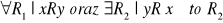
   - jest stosunkiem odwrotnym

2. Stosunki symetryczne, asymetryczne i nonsymetryczne

1. Symetryczne - takie które zachodzą zarówno pomiędzy poprzednikiem a następnikiem i na odwrót (np. pokrewieństwo)

2. Asymetryczne - jeżeli zachodzi pomiędzy poprzednikiem i następnikiem a NA PEWNO NIE ZACHODZI na odwrót

3. Nonsymetryczne - stosunek zachodz pomiędzy poprzednikiem a następnikiem lecz nie wiadomo jak zachodzi na odwrót

3. Stosunek przechodni

1. Stosunek przechodni - jeżeli x > y, y > z to na pewno x > z

4. Stosunek porządkujący i równościowy w danej klasie przedmiotów

1. Stosunek spójny w danej klasie przedmiotów - kiedy stosunek zachodzi pomiędzy dowolnie wybranymi elementami danej klasy

2. Stosunek porządkujący - pozwalający wszystkie elementy danej klasy ustawić według danego kryterium, musi być więc zarazem stosunkiem przechodnim i asymetrycznym oraz spójnym w danej klasie przedmiotów

3. Stosunek zwrotny - zachodzący pomiędzy dowolnym elementem danej klasy oraz samym sobą (np. każdy człowiek jest rówieśnikiem samego siebie)

4. Stosunek równościowy - taki który jest zarazem przechodni symetryczny oraz zwrotny w danej klasie

7

---