Smutkowska Agnieszka

Marek Sebastian

Pancerz Mariusz

Grupa W 101

ĆWICZENIE 66

Temat: Wyznaczanie stałej Plancka

1. Wstęp Teroetyczny

Według M. Plancka energia zmienia się nie w sposób ciągły, lecz porcjami - kwantami energii. Energia kwantu jest wprost proporcjonalna do częstotliwości emitowanego promieniowania.

E = h⋅ν

h-stała Plancka; h=6,6249⋅10^-34 [J⋅s]

Prawo Kirchoffa:

e(ν,T) / a(ν,T) = ε(ν,T)

e(ν,T) - zdolność emisyjna

a(ν,T) - zdolność absorbcyjna

ε(ν,T) - zdolność emisyjna ciała doskonale czarnego

Prawo Stefana-Boltzmana:

Całkowita energia E wypromieniowana przez jednostkową powierzchnię w czasie 1 s jest proporcjonalna do czwartej potęgi temperatury.

E = σ ⋅ T⁴

σ =5,67⋅10^-8 W/m²k² (stała Stefana-Boltzmana)

T - temperatura w skali kelwina.

Prawo Wiena:

V_max = const.⋅T

V_max-częstotliwość, przy której zdolność emisyjna przyjmuje wartość maksymalną.

Wykorzystując równanie Einsteina-Millikana można wyznaczyć stałą Plancka:

h ⋅ ν = W + E_kmax

Do wyznaczenia stałej Plancka wykorzystamy zjawisko fotoelektryczne zewnętrzne, polegające na emisji elektronów z metalu pod wpływem padającego światła.

A

V

K

A

Z

Źródłem światła monochromatycznego (Z) oświetlamy katodę (K) z której emitowane są elektrony. Pomiędzy fotokatodę i anodę przykładamy napięcie hamujące. Woltomierz mierzy napięcie hamujące natomiast amperomierz mierzy prąd anodowy. Maksymalna energia kinetyczna E_kmax=e⋅U₀, gdzie e-ładunek elektronu; e=1,6⋅10^-19 C, natomiast przez U₀ oznaczymy wartość napięcia hamującego, przy którym prąd anodowy jest równy 0

Podstawiając e⋅U za E_kmax do równania Einsteina-Millikana otrzymujemy, że:

eU₀ = h ⋅ ν - W

Wykres napięcia hamującego U₀ w funkcji częstotliwości ν jest funkcją liniową
y = ax + b o współczynnikach a = h/e ; b = - W/e. Znając a i b możemy wyznaczyć stałą Plancka oraz pracę wyjścia elektronu z metalu.

2. Metoda i przebieg ćwiczenia

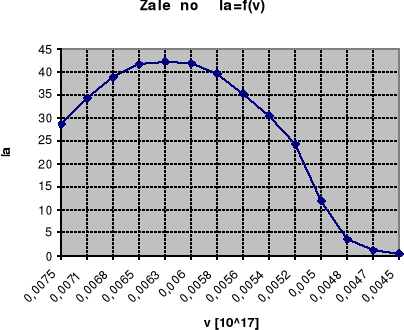
Jako pierwsza została wyznaczona zależność prądu fotoelektrycznego od (częstości ν) długości fali λ padającego promieniowania.

Zależność I=f(n)

λ	nm	400	420	440	460	480	500	520
ν [10^17]	Hz	0,0075	0,0071	0,0068	0,0065	0,0063	0,0060	0,0058
Ia	nA	28,63	34,29	38,75	41,64	42,20	41,92	39,67

λ	nm	540	560	580	600	620	640	660
ν [10^17]	Hz	0,0056	0,0054	0,0052	0,0050	0,0048	0,0047	0,0045
Ia	nA	35,30	30,32	24,25	11,96	3,65	1,24	0,48

gdzie:

U - spadek napięcia na rezystorze R=2,9 MW;

I - prąd fotoelektryczny;

λ - długość fali padającego promieniowania;

ν - częstość fali padającego promieniowania;

W drugiej kolejności zostały wyznaczone maksymalne napięcie hamowania U_h, którym towarzyszą zerowe prądy fotoelektryczne I dla stałych wartości długości fali λ padającego promieniowania.

Zależność I=f(U_h)

λ=400 nm		λ=450 nm		λ=500 nm		λ=550 nm		λ=600 nm
Uh	Ia	Uh	Ia	Uh	Ia	Uh	Ia	Uh	Ia
V	mA	V	mA	V	mA	V	mA	V	mA
0	67,5	0	96,0	0	64,9	0	77,8	0	27,7
0,1	49,7	0,1	66,3	0,1	37,2	0,1	45,6	0,1	12,7
0,2	34,2	0,2	43,1	0,2	18,4	0,2	22,0	0,2	4,4
0,3	24,6	0,3	26,8	0,3	6,7	0,3	7,4	0,3	0,8
0,4	17,5	0,4	15,1	0,4	2,1	0,4	1,5	0,4	0
0,5	12,2	0,5	7,8	0,5	0,4	0,5	0,1
0,6	8,2	0,6	3,5	0,66	0	0,52	0
0,7	5,1	0,7	1,2
0,8	2,8	0,8	0,1
0,9	1,2	0,83	0
1	0,4
1,09	0

W kolejnym kroku została wyznaczona zależność maksymalnego napięcia hamującego U_h0 od częstości padającego promieniowania ν.

Zależność U_h0=f(n)

λ	nm	400	450	500	550	600
Uh0	V	1,09	0,83	0,66	0,52	0,4

Wykorzystując program komputerowy obliczyliśmy współczynniki a i b funkcji liniowej: V = aν + b.

a = 267,72⋅10^-17 b = -0,934

Δa = 9,7183 Δb = 0,0192

Z zależności iż a=h/e możemy wyznaczyć stałą Plancka:

a = h / e ⇒ h = a⋅e

gdzie h -stała Plancka, e - ładunek elektronu; (e = 1,602⋅10^-19 C)

h = a ⋅ e = 2,677191 ⋅ 10^-19 ⋅ 1,602⋅10^-19 [C] = 4,28 ⋅ 10^-34 J⋅s

Stała Plancka z doswiadczenia wynosi:

h = 4,28 ⋅ 10^-34 J⋅s

Stała Plancka Teoretyczna wynosi:

h = 6,62 ⋅ 10 ^-34 J⋅S

Pracę wyjścia elektronu z metalu możemy obliczyć z zależności:

b = -W / e ⇒ W = - b ⋅ e

W = 0,934 ⋅ 1,602⋅10^-19 J = 1,49⋅10^-19 [J]

Praca wyjścia elektronu z metalu wynosi:

W=1,49⋅10^-19 J

Wnioski:

Błąd wyniku spowodowany jest niedokładnością przyrządów pomiarowych oraz niewystarczającymi warunkami do przprowadzenia tak dokładnych pomiarów, mimo to powyższe doświadczenie pozwala zaznajomic się ze zjawiskiem fotoelektrycznym. Można sie było przekonać o liniowej zależności napięcia hamującego od częstości padającego promieniowania.

Ćw. 66 Wyznaczanie Stałej Plancka

6

---