LABORATORIUM PODSTAW MIERNICTWA
ĆWICZENIE NR 5
POMIARY NAPIĘĆ ZMIENNYCH
Patryk Wołowicz EiT sem 2
Pomiar charakterystyki diody oraz rezystancji amperomierza.
Pomiaru charakterystyk dokonałem w odpowiednim układzie określając jakie napięcie odłoży się na diodzie przy danym wymuszeniu prądowym, co przedstawia tabela:
Tabela 1
ID |
mA |
0,2 |
0,5 |
1 |
1,5 |
2 |
2,5 |
UD |
V |
0,4972 |
0,5361 |
0,5676 |
0,5864 |
0,6 |
0,6104 |
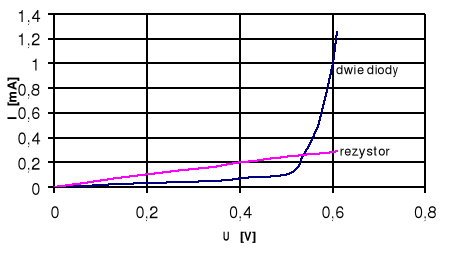
Aby wykreślić charakterystykę I-U woltomierza prostownikowego mostkowego muszę zsumować charakterystyki 2 diod oraz obciążenia R=2kΩ+RA. Ponieważ zmierzona rezystancja miliamperomierza wynosi 78,56Ω, więc obciążenie R=2078,5Ω.
Zauważmy, że połączenie szeregowe dwóch diod spowoduje zmniejszenie się prądu przepływającego o połowę. Ponieważ tabela 1 określa zależność I-U dla pojedynczej diody, dlatego trzeba to wziąć pod uwagę.
Wprowadzenie do szeregu rezystancji R=2078,5Ω spowoduje dalsze zmniejszenie się prądu.
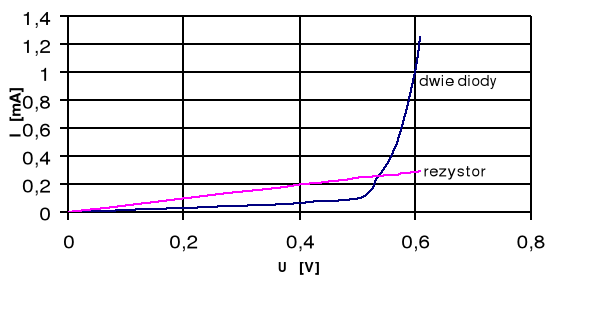
Ostatecznie zależność prądu i napięcia dla układu dwóch diod i rezystancji R pokazuje wykres i tabela:
Tabela 2
U |
V |
0,4972 |
0,5361 |
0,5676 |
0,5864 |
0,6 |
0,6104 |
I2D |
mA |
0,1 |
0,25 |
0,5 |
0,75 |
1 |
1,25 |
IR |
mA |
0,239211 |
0,257926 |
0,273082 |
0,282127 |
0,28867 |
0,293673 |
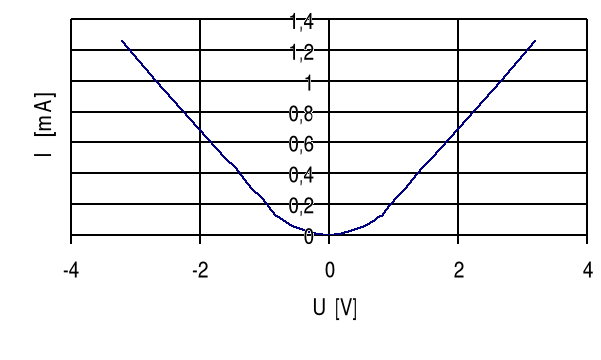
Jeżeli teraz dodamy do siebie charakterystyki diod oraz rezystancji szeregowej względem prądu I, pamiętając, że woltomierz prostownikowy mostkowy jest woltomierzem przewodzącym symetrycznie w obu kierunkach, to otrzymamy końcową zależność I-U:
Skalowanie woltomierza prostownikowego z przetwornikiem wartości średniej.
Celem tego ćwiczenia jest skalowanie woltomierza w wartościach skutecznych dla sygnału sinusoidalnego. Skalowałem woltomierz prostownikowy mostkowy, którego konstrukcja opiera się na bazie mostka Graetz'a. Wyniki podano w poniższej tabeli:
Tabela 3
I |
MA |
0,2 |
0,5 |
1 |
1,5 |
2 |
2,5 |
U |
V |
1,368 |
2,196 |
3,482 |
4,714 |
5,901 |
7,088 |
Obserwacja i pomiary napięć w układzie mostkowym woltomierza prostownikowego za pomocą oscyloskopu.
Korzystając z układu pomiarowego z poprzedniego ćwiczenia i podając na amperomierz prąd I=2,5 mA zbadałem kształt i amplitudę napięć U12, U13, U34. Umiejscowienie punktów przedstawia schemat na następnej stronie:
Rys 1. Schemat układu woltomierza prostownikowego
Otrzymane wyniki zawarte są w tabeli:
Tabela 4
|
|
U12 |
U13 |
U34 |
y |
[cm] |
2 |
2 |
2 |
Dy |
[V/cm] |
5 |
5 |
5 |
U |
[V] |
10 |
10 |
10 |
Jak widać amplitudy wszystkich sygnałów są jednakowe, natomiast ich kształt wygląda następująco:
U12 U13 U34
Jedynie sygnał U12 jest bipolarny, pozostałe dwa są unipolarne. Sygnał U13 przenosi pół okresu sygnału U12, sygnał U34 - to sygnał U12 po wyprostowaniu na mostku.
Rezystancja wejściowa skuteczna woltomierza z przetwornikiem wartości średniej.
Sposób pomiaru rezystancji jest następujący. Dołączam do woltomierza równolegle rezystor dekadowy i tak reguluje jego rezystancją, aby przez woltomierz płynęła połowa prądu wchodzącego do układu. Wówczas rezystor dekadowy pokaże mi rezystancję wejściową skuteczną woltomierza.
Posługując się tym sposobem otrzymałem wynik:
Rwe sk=2051 Ω.
Skalowanie woltomierza prostownikowego z przetwornikiem wartości szczytowej.
Celem tego ćwiczenia jest skalowanie woltomierza w wartościach skutecznych dla sygnału sinusoidalnego. Wyniki pomiarów zostały przedstawione w tabeli:
Tabela 5
I |
mA |
0,2 |
0,5 |
1 |
1,5 |
2 |
2,5 |
U |
V |
0,724 |
1,262 |
2,127 |
3,005 |
3,832 |
4,681 |
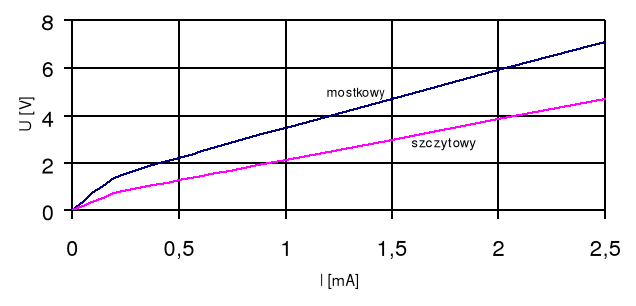
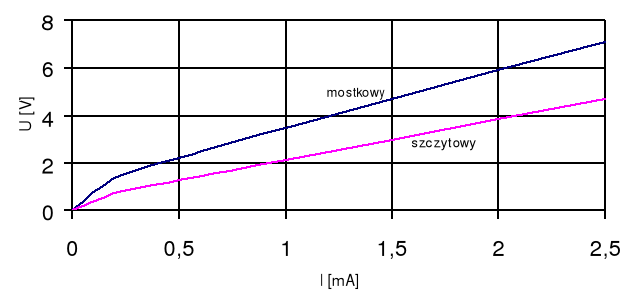
Poniższy wykres zawiera krzywe skalowania U=f(I) dla woltomierza prostownikowego mostkowego z przetwornikiem wartości średniej oraz woltomierza prostownikowego z przetwornikiem wartości szczytowej:
Obserwacja amplitudy i kształtu napięcia w woltomierzu z przetwornikiem wartości szczytowej.
Korzystając z oscyloskopu mogę obserwować zarówno kształt jak i amplitudę przebiegów, co prezentuje tabela:
Tabela 6
|
|
Uwe |
UD |
Ui ład |
ΔUc (1μF) |
ΔUc (10μF) |
Y |
[cm] |
1,5 |
2,5 |
4 |
1,4 |
0,8 |
Dy |
[V/cm] |
5 |
5 |
0,05 |
2 |
0,5 |
U |
[V] |
7,5 |
12,5 |
0,2 |
2,8 |
0,4 |
oraz kształty poszczególnych napięć:
Uwe UD
Ui ład
Pomiar modułu impedancji wejściowej woltomierza V-640.
Do woltomierza podłączamy generator i ustalam na jego zaciskach napięcie 5V. Następnie dołączam szeregowo z generatorem rezystancję R=1MΩ i sprawdzam jakie napięcie ustaliło się na woltomierzu.
Na podstawie takich danych mogę obliczyć moduł impedancji wejściowej woltomierza przy założeniu stałości napięcia na generatorze. Wówczas:
Ua=J(|Z|+R), Ub=J|Z|,
|Z|= UbR/(Ua-Ub)
Powyższe rozważania zawiera tabela:
Tabela 7
f |
Ua |
Ub |
|Z| |
1 kHz |
5 V |
4,9 V |
49 MΩ |
10 kHz |
5 V |
2,5 V |
1 MΩ |
Pomiar napięcia wielkiej częstotliwości.
Na wyjściu generatora przy częstotliwości 1kHz ustawiam napięcie 4V. Następnie zwiększam częstotliwość do 500kHz i dokonuję pomiaru bez oraz z użyciem sondy.
Tabela 8
f |
Sposób pomiaru: |
Wynik: |
1 kHz |
bezpośrednio |
4 V |
500 kHz |
bezpośrednio |
0,7 V |
500 kHz |
za pomocą sondy w.cz. |
3,9 V |
Jak widać pomiar bezpośredni przy wysokich częstotliwościach jest przekłamany. Względny błąd pomiaru bezpośredniego dla f=500 kHz wynosi:
δ=82,5 %,
gdy dla pomiaru z wykorzystaniem sondy:
δ=2,5 %,
czyli jest aż 33 razy mniejszy.
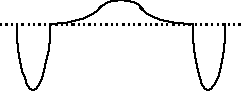
Pomiar przebiegów odkształconych.
Tym razem dokonałem pomiaru napięcia skutecznego przebiegu sinusoidalnego, trójkątnego oraz prostokątnego. W tym celu wykorzystałem przetwornik RMS/DC oraz multimetr cyfrowy M-4650, który mierzy wartość średnią.
![]()
Jeżeli mierzę przebiegi trójkątne lub prostokątne miernikami wyskalowanymi w wartościach sinusoidalnych, to muszę wprowadzić poprawkę, która skoryguje moje wyniki na prawidłowe. Odpowiednie mnożniki poprawkowe obliczam ze wzoru:
gdzie Fx: współczynnik kształtu dowolnego przebiegu,
F: współczynnik kształtu przebiegu sinusoidalnego.
Wartości mierzone przez przetwornik RMS/DC można uznać za poprawne. Wartości podawane przez multimetr M-4650 należy przemnożyć przez wartości k. Wyniki przedstawia tabela:
Tabela 9
Kształt: |
URMS/DC [mV] |
UM-4650 [mV] |
k |
Urzecz [mV] |
Sinusoidalny |
100 |
97,4 |
1 |
97,41 |
Trójkątny |
83 |
78,44 |
1,04 |
81,6 |
Prostokątny |
150,9 |
164,9 |
0,9 |
148,4 |
10. Pomiary przebiegów wolnozmiennych.
W ćwiczeniu tym dokonałem pomiaru okresu i międzyszczytowej wartości napięcia wolnozmiennego przebiegu sinusoidalnego, trójkątnego i prostokątnego, wytwarzanych przez generator. Pomiar dokonywany był w czasie rzeczywistym poprzez multimetr cyfrowy sprzężony z komputerem, który wydrukował odpowiedni wykres. Okres i wartość międzyszczytową odczytałem z tego wykresu:
Sygnał sinusoidalny:
długość okres - 94s
wartość międzyszczytowa - 6,3 V
Sygnał prostokątny:
długość okresu - 95s
wartość międzyszczytowa - 6,5 V
Sygnał trójkątny:
długość okresu - 94s
wartość międzyszczytowa - 6,2 V
Powyższe wartości mogą być obarczone sporym błędem, ponieważ wykres był bardzo niedokładny.
11. Właściwości metody pomiaru amplitudy i częstotliwości napięć sinusoidalnych za pomocą trzech próbek.
Metoda pomiaru polega na pobraniu trzech próbek jednego okresu sinusoidy.
Próbki te mogą być pobrane w ułamku czasu trwania okresu, a więc sam pomiar może być wykonany w czasie krótszym niż jeden okres. Jest to ogromna zaleta tej metody.
Metoda ta ma jednak także wady. Po pierwsze dokładność określenia amplitudy i częstotliwości zależy od tego, w jakim miejscu pobiorę owe próbki. Jeżeli próbki zostaną pobrane, gdy sygnał znajduje się w okolicach położenia równowagi, to otrzymam wyniki obarczone dużym błędem. Natomiast gdy próbkuję sygnał znajdujący się w pobliżu ekstremum, to błąd jest minimalny.
Po drugie dokładność próbkowania i błąd próbkowania związane są z ilością poziomów próbkowania, a więc z ilością bitów przeznaczonych na jedną próbkę.(Oczywiście zakładając, że kolejne poziomy rozłożone są równomiernie.) Praktycznie słowa 6-bitowe zapewniały już dość dobrą jakość sygnału odtwarzanego na ich podstawie. Program który testowałem pozwalał nawet na 20-bitową rozdzielczość przetwornika.
Po trzecie istotny wpływ na błąd metody ma występowanie kolejnych harmonicznych. Kolejne harmoniczne zniekształcają sygnał pierwotny, co w metodzie trzech próbek może powodować duże błędy.

1
2
4
3
mA
![]()
Wyszukiwarka
Podobne podstrony:
NO4 MULTIMETR CYFROWY, MR4 OPR, Patryk Wołowicz
NO5 NAPIECIA ZMIENNE, lab mier5, Pomiar pierwszy
NO5 NAPIECIA ZMIENNE, MRN5, 2) Opracowanie
NO5 NAPIECIA ZMIENNE, MIERNIK5, WYDZIA˙ ELEKTRONIKI
Pomiary napiec zmiennych id 374 Nieznany
Ćw2 Pomiary multimetryczne parametrów napięcia zmiennego
Pomiar napięćokresowo zmiennych
6 Zadania 6 Pomiar napięć zmiennych
5 napieci zmienne cw5 id 60977 Nieznany (2)
W12 Pomiary parametrów napięć zmiennych ppt
Zasilacze, Zasilacz komputera zamienia napięcie zmienne dostępne w sieci elektrycznej na cały zestaw
spr elektro pomiery napiec zmiennych
Napięcie zmienne za osc
Żarzenie lamp napięciem zmiennym i stałym
napiecia zmienne
Pomiar napięć zmiennych 2003 10 15
więcej podobnych podstron