z1. Ile gramów Ca₃(PO₄)₂ rozpuści się w 100g wody?. K_SO Ca₃(PO₄)₂ = 10^-26

W takim zadaniu należy rozpisać dysocjację trudno rozpuszczalnej soli, napisać wyrażenie na iloczyn a następnie zastanowić się, jakiego typu jest to iloczyn:

Ca₃(PO₄)₂ ↔ 3Ca²⁺ + 2PO₄^3-

x 3x 2x

K_SO = [Ca²⁺]³[PO₄^3-]² = (3x)³*(2x)² = 108x⁵

O co chodzi z tym x:

Zakładamy, że dysocjuje x moli tej soli. Na skutek dysocjacji dostajemy 3x moli jonów Ca²⁺ i 2x moli jonów PO₄^3-. Jeżeli te x wstawimy do odpowiednich nawiasów kwadratowych, to ostatecznie otrzymamy wyrażenie 108x⁵.

x =
=
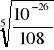
= 2,47*10^-6 mola

Czyli w 1000 cm³ wody może się rozpuścić 2,47*10^-6 mola Ca₃(PO₄)₂, a więc w 100 cm³ (100g) wody 10 razy mniej czyli 2,47*10^-7 mola.

M (Ca₃(PO₄)₂ = 310 g/mol

A więc m = 2,47*10^-6*310 = 7,66*10^-4g

z. 2. Czy przy pH = 4 z 0,1M roztworu CuCl₂ może się wytrącić wodorotlenek miedzi? K_SO Cu(OH)₂ = 2,5*10^-19

Na początku trzeba zapisać dysocjację trudno rozpuszczalnego związku i wyrażenie na iloczyn:

Cu(OH)₂ ↔ Cu²⁺ + 2OH^-

K_SO = [Cu²⁺][OH^-]²

Nie ma sensu wpisywać tu jakichkolwiek x-sów i zastanawiać się jakiego typu to jest iloczyn. W takich zadaniach do formuły na iloczyn, czyli wzoru [Cu²⁺][OH^-]² należy wstawić stężenia obu jonów, wyliczyć wartość liczbową i porównać ją z tablicową wartością iloczynu rozpuszczalności. Jeżeli liczba, która nam wyszła jest większa od K_SO, to osad się strąci, a jeżeli jest mniejsza od K_SO, to osad się nie strąci.

W tym zadaniu znamy zarówno stężenie jonów Cu²⁺ - w treści zadania napisane jest, że CuCl₂ jest 0,1M, jak i stężenie jonów OH^-, bo znamy pH:

pH = 4; pOH = 10; [OH^-] = 10^-10

Podstawiamy do formuły na iloczyn:

[Cu²⁺][OH^-]² = 0,1*(10^-10)² = 10^-21

Zauważamy, że liczba, która nam wyszła, 10^-21 jest mniejsza od 2,5*10^-19 (K_SO), czyli wyciągamy wniosek, że osad się nie strąca.

z. 3. Zbudowano ogniwo Daniela zestawione z półogniwa glinowego i półogniwa talowego. E⁰(Al³⁺/Al⁰) = -1,66 V;

E⁰(Tl⁺/Tl⁰) = -0,336 V. Wiedząc, że stężenie jonów glinu wynosiło 0,4 mol/dm³, a jonów talu 0,02 mol/dm³:

a) Napisz schemat tego ogniwa

b) Zapisz reakcje zachodzące w półogniwach (po złączeniu ich w to konkretne ogniwo) i reakcje sumaryczną.

c) Oblicz stałą równowagi dla reakcji zachodzącej w ogniwie

d) Za pomocą odpowiednich wzorów wyraź siłę elektromotoryczną tego ogniwa a następnie oblicz jej wartość.

e) Zapisz wyrażenia na potencjały obu półogniw i oblicz ich wartość przy zadanych stężeniach jonów.

f) Oblicz zmianę entalpii swobodnej w tym ogniwie, jeżeli przez obwód przepłynęło 0,1 mola elektronów.

a) (A-) -Al| Al³⁺ || Tl⁺ |Tl⁺ (K+)

b) Al⁰. - 3e^- → Al³⁺

Tl⁺ + e^- → Tl⁰ |*3

Al. + 3Tl⁺ ↔ Al³⁺ + 3Tl

c) K = [Al³⁺]/[Tl⁺]³ = (0,4)/(0,02)³ = 50000

d) SEM = E⁰_Tl+/Tl - E⁰_Al3+/Al. - (0,059/3)logK = -0,336 - (-1,66) - 0,02log(50000) =

1,324 - 0,094 = 1,230 V

e) Pamiętamy, że rozpięte półogniwa rozpatruje się zawsze w kierunku redukcji:

Al³⁺ + 3e^- ↔ Al⁰ ; K = 1/[Al³⁺]

E = E⁰_Al3+/Al. - (0,059/3)logK = -1,66-0,008 = -1,668V

Tl⁺ + e^- ↔ Tl⁰, K = 1/[Tl⁺]

E = E⁰_Tl+/Tl - 0,059logK = -0,336 - 0,1 = -0,436V

f) ΔG = -nFSEM = -0,1*96500*1,23 = -11869 J

z. 4. Zbudowano dwa półogniwa: W roztworze zawierającym jony kobaltu (III) (stężenie 0,04M) i jony kobaltu (II) (stężenie 0,3M) zanurzono elektrodę platynową. Podobnie w drugim roztworze zawierającym jony cyny (IV) (stężenie 0,15M) i cyny (II) (stężenie 0,05M) zanurzono elektrodę platynową. Elektrody połączono drutem a roztwory kluczem elektrolitycznym łącząc te półogniwa w ogniwo prądu stałego. E⁰_Co3+/Co2+ = 1,84V; E⁰_Sn4+/Sn2+ = 0,15V. Wykonaj następujące polecenia:

a) Zapisz schemat tego ogniwa.

b) Zapisz reakcje zachodzące w półogniwach (po złączeniu ich w to konkretne ogniwo) i reakcję sumaryczną.

c) Oblicz stałą równowagi dla reakcji zachodzącej w ogniwie.

d) Za pomocą odpowiednich wzorów wyraź siłę elektromotoryczną tego ogniwa i oblicz jej wartość.

e) Zapisz wyrażenia na potencjały obu (separowanych) półogniw i oblicz ich wartość przy zadanych stężeniach jonów.

f) Oblicz zmianę entalpii swobodnej w tym ogniwie, jeżeli przez obwód przepłynęło 0,3 mola elektronów.

a) (A-) -Pt| Sn²⁺, Sn⁴⁺ || Co²⁺, Co³⁺ |Pt+ (K+)

Uwaga!! Zapis -Pt| Sn²⁺| Sn⁴⁺ || Co²⁺| Co³⁺|Pt+ jest zupełnie błędny - kreski pionowe oznaczają granicę faz, przecież jony Sn²⁺ i Sn⁴⁺ nie są niczym od siebie odseparowane i pływają razem w jednym roztworze, podobnie jony kobaltu. Tu muszą być przecinki! Nie ma natomiast znaczenia kolejność wymieniania jonów w roztworze, czyli Sn⁴⁺, Sn²⁺ albo Sn²⁺, Sn⁴⁺.

b)

Sn²⁺ - 2e^- → Sn⁴⁺

Co³⁺ + e^- → Co²⁺ |*2

Sn²⁺ + 2Co³⁺ ↔ Sn⁴⁺ + 2Co²⁺

c)

K =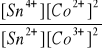
=
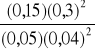
= 169

d)

SEM = E⁰_Co3+/Co2+ - E⁰_Sn4+/Sn2+ -(0,059/2)log(K) = 1,84 - 0,15 - 0,0295log(169) = 1,69 - 0,066 = 1,624V

e)

Sn⁴⁺ + 2e^- ↔ Sn²⁺; K = [Sn²⁺]/[Sn⁴⁺]

E= E⁰_Sn4+/Sn2+ - (0,059/2)logK = 0,15 - 0,0295log(0,333) = 0,15 + 0,014 = 0,164V

Co³⁺ + e^- ↔ Co²⁺ K = [Co²⁺]/[Co³⁺]

E = E⁰_Co3+/Co2+ - 0,059logK = 1,84 - 0,059log(7,5) = 1,84 - 0,05 = 1,79V

f) ΔG = -nFSEM = -0,3*96500*1,624 = 47015J

---